Screen shot #13 (Merely a picture to illustrate that our
GUI is totally self-explanatory)
TK-MIP’s underlying Software Architecture
can be reconfigured to match the structure of your application.
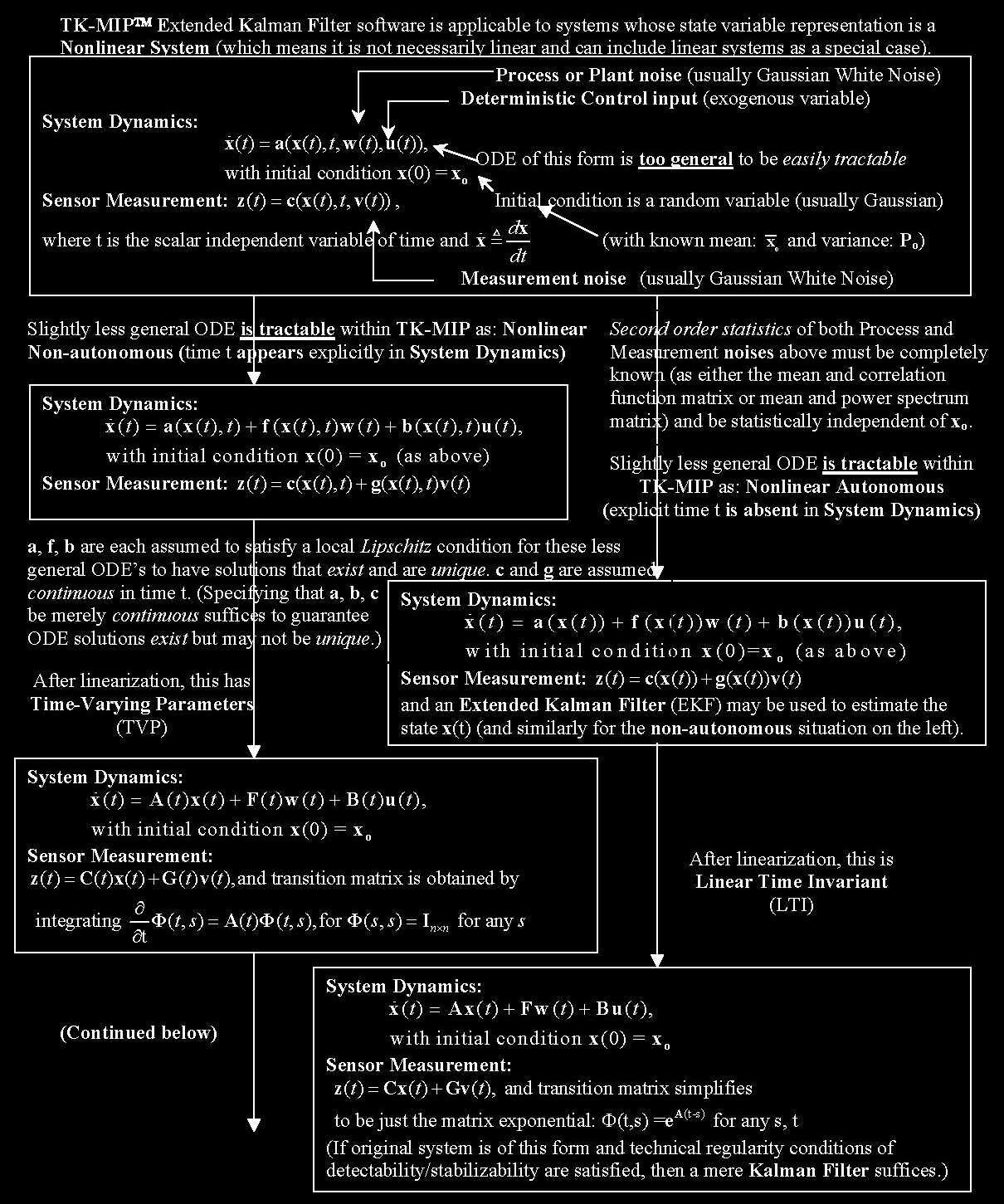

The flowchart above provides insights into how TK-MIP may best be reconfigured for most efficient processing to accommodate specific application
structural simplifications. For situations involving time stamps used in data logging, let
the above defined symbol delta: Δ = t(j+1) - tj.



The best or clearest discussion of the proper sequence of discrete-time KF operations (to be implemented into software) that
we have encountered to date is found on pages 234-236 of
Brown, Robert Grover, Hwang, Patrick Y. C., Introduction to Random Signals and Applied Kalman
Filtering, 2nd Edition, John Wiley & Sons, Inc., New York, 1983, 1992.
They also discuss an alternate formulation for implementing a discrete-time KF
into software in Section 6.2 on pages 259-261 that is also correct but looks a little
different. [They also provide an excellent derivation and discussion of D. T.
Magill’s earlier 1965 Multiple Model of Magill (MMM) bank-of-Kalman-Filters approach to adaptive filtering
{also called the Multiple Model Estimation Algorithm
(MMEA)} in Section 9.3 of
this wonderfully clear and insightful book.

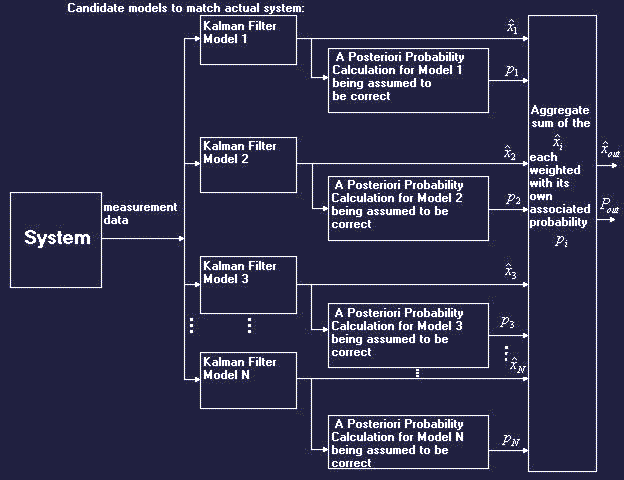

Magill's 1965 approach predated the Interactive Multiple
Model (IMM) of Prof. Bar-Shalom (UCONN) and Prof. X.-Rong Li
but it did not possess their lucrative and useful additional "bells
and whistles", namely, IMM is potentially more responsive to changes
by being willing to continue entertaining the several alternative filter model candidates that were hypothesized and enunciated as candidate models by virtue of the
presence of the
"sojourn time" and the "finite state Markov
chain transition probabilities" that keeps the several alternative candidate filter models viable and active.
Prof. Bar-Shalom, himself has warned that some people don't like the answers from
IMM because, instead of yielding "black or white" selections or decisions as
to the appropriate underlying model by picking only one of the specified
candidate models enunciated in the figure above, IMM instead yields
"shades of gray" by deciding on a final result that blends aspects of several of the underlying candidate models together as one.
This consequential outcome is satisfactory for some applications but
disappointing for other applications, depending on the application.]
Kalman
Filter Structure for handling the automatic processing of two different periodic
measurement streams (of different periods) from different types of measurement
structures and quality (demonstrated here using MatLab).
Go to Top