TeK Associates Capabilities:
Knowledge of operational principles and behavior of INS
gyros and accelerometers and likewise for GPS: Familiar with their
underlying state variable error models and INS calibration
procedures and typical failure modes and interactions.
A clear simple
overview (that appeared on the Internet on 1 January 2019) that offers an
understanding of INS concerns is available here by clicking on it.
The future of GPS and GNSS that appeared on the Internet is provided here
by clicking on it.
https://www.af.mil/News/Article-Display/Article/1722633/first-gps-iii-satellite-successfully-launched/
http://gpsworld.com/directions-2018-resiliency-key-to-new-gps/
--The first satellite in the new GPS III constellation blasted off in late
December 2018 on a SpaceX Falcon 9 rocket at Cape Canaveral – Harris technology is on board, as it has been on every launch for the last 40 years.
--Lockheed Martin provides the satellite, and Harris navigation technology generates the GPS signal that billions of people depend on everyday.
Harris technology has been on more than 70 GPS satellite payloads, including the 31 GPS satellites moving through space today.
Harris says that they are looking forward to a continued partnership on future GPS III satellite launches.
--Harris congratulates the United States Air Force, Lockheed Martin, and SpaceX on
the successful GPS III launch.
“Special thanks go to the dedicated Harris employees
at their Clifton, NJ facility who develop this amazing technology. Learn more about Harris’ role in the GPS mission here:
http://bit.ly/2Ta0ELt ”
https://phys.org/news/2018-03-nist-first-ever-spectrum-military-wireless.html?utm_source=menu&utm_medium=link&utm_campaign=item-menu
https://www.wsj.com/articles/how-to-defend-against-gps-spoofing-attacks-1537306495
Map of GPS Control Segment: https://www.gps.gov/multimedia/images/GPS-control-segment-map.pdf
Satellites being reported in view, as seen from the GPS
Project Office, at a fixed location within CONUS (as the earth rotates and as
the satellites move in their respective 6 orbital planes).
Realistically, the GPS receiver can move and the platform upon
which it is based can move also (like a person with a GPS-equipped cell phone walking on
a ferry boat sailing from Manhattan, NY to Staten Island).
GPS interference:
https://www.faa.gov/documentLibrary/media/Notice/GENOT_7110_711_EMB-300.pdf
Space Command Calls Out Russia for Anti-Satellite Test:
https://www.satellitetoday.com/government-military/2020/04/16/space-command-calls-out-russia-for-anti-satellite-test/
Air Force’s Joint Forces Space Component Command Missions to Move to U.S. Space
Command.
GPS interference Solutions:
https://www.gps.gov/governance/advisory/meetings/2018-05/holmes.pdf
Sophisticated Spoofing of GPS:
https://www.linkedin.com/pulse/spoofing-gps-your-maps-next-level-danger-forbes-dana-a-goward/
https://www.forbes.com/sites/thomasbrewster/2018/07/12/google-maps-gps-hack-takes-victims-to-ghost-locations/amp/
https://www.bleepingcomputer.com/news/security/researchers-mount-successful-gps-spoofing-attack-against-road-navigation-systems/
http://rntfnd.org/wp-content/uploads/Smart-Grid-and-GPS-Time-MITRE.pdf
http://rntfnd.org/wp-content/uploads/Electric-Power-Timing-Applications-MITRE.pdf
http://rntfnd.org/2015/12/10/us-to-build-eloran-timing-then-navigation-network-to-complement-gps/
https://www.prweb.com/releases/sae_international_issues_transmitted_enhanced_loran_signal_standards/prweb15770639.htm
New GPS ‘circle spoofing’ moves ship locations thousands of miles:
https://www.gpsworld.com/new-gps-circle-spoofing-moves-ship-locations-thousands-of-miles/
https://rntfnd.org/2020/05/26/video-skytruth-presenation-rnt-foundation-annual-meeting/
https://www.youtube.com/watch?v=33AlxsUEin4&feature=youtu.be&t=1
GPS jamming on agenda as Russian defence delegation sat down for talks in Oslo:
https://thebarentsobserver.com/en/security/2019/03/gps-jamming-agenda-russian-defence-delegation-sits-down-talks-oslo
Size of GPS Jammer markets: https://www.transparencymarketresearch.com/signal-jammer-market.html
https://www.arl.army.mil/www/default.cfm?article=3301
Power of THOR ready to down enemy drones - GPS World:
The Air Force Research Laboratory (AFRL) developed a counter-swarm high-power weapon to deter enemy drones —
THOR.
Learn more about the weapon, which provides non-kinetic defeat of multiple targets. (Photo:
AFRL) #AFRL weapon #drone
https://www.gpsworld.com/power-of-thor-ready-to-down-enemy-drones/
Please click on the link to see: 7 Deadly Sins of Innovation in the Age of
AI
3 Things You Need to Know About Artificial Intelligence:
https://medium.com/mathworks/3-things-you-need-to-know-about-artificial-intelligence-7c15b3853781
Public-private partnership to launch eLORAN technology to back-up and accompany GPS - Intelligent Aerospace:
https://www.intelligent-aerospace.com/home/article/14181475/eloran-loran-c-gps-gnss
International Civil Aviation Org Issues Advisory on GNSS Disruption (Finally!)
In September, 2019, it was reported how airline and pilot groups had raised the issue of
GNSS disruption to the UN's International Civil Aviation
Organization (ICAO).
The body decided it was an urgent issue (since airplanes have almost crashed because of
GNSS disruption, after all) and they decided to act promptly.
The result was a letter to member states published today:
https://rntfnd.org/wp-content/uploads/ICAO-Letter-GNSS-Resilience-Aug-2020.pdf
A few thoughts before you get too discouraged about why it took so long for ICAO to act:
ICAO is an international body and they can't do anything quickly. The only real power
ICAO has is to bring nations together to talk and provide them information. It
can't do much more than merely inform. For things to happen, nations have to start changing the way they do business.
Most all the member states had all the information already. This is just nudging them to act in ways they already know
that they should. The list of things ICAO recommends nations do is a pretty good one. If any nations pay attention and do some or all they will be better off than before.
When we do have a major air crash because of GNSS disruption this will be a list of good practices for people to look at and adopt to help prevent it happening again.
Editorial Advisory Board PNT Q&A: Opportunities with GNSS correction services - GPS World:
New players are offering GNSS correction services — pushing prices down and offering new business models. What opportunities does this open up?
https://www.gpsworld.com/editorial-advisory-board-pnt-qa-opportunities-with-gnss-correction-services/
GPS Disruptions Varied, Widespread - Reports to the US Government:
RNTF Report:
Very few people know how to report problems with GPS reception. And few of those take the trouble to do it. So the listing that the US government maintains of GPS disruption reports really represents the tip of the iceberg. Likely only the most sophisticated and diligent users, often with the most persnickety problems, appear on the website.
We like to check in on the listing periodically and see what kinds of things have shown up. The reports so far in 2020 have been a varied collection.
There are always a number of problems that the government says are due to "user equipment." Interestingly, problems due to week rollover are still being reported, along with the usual number of receivers that needed updating or had another sort of problem.
In February and July of this year there were problems with the GPS ground control system that caused the information broadcast to contain minor errors. These was detected and reported by some sophisticated users and acknowledged by the Air Force's GPS Operations Center. The web page, which goes back as far as 2017, shows similar events in February and November of 2018, and in May of 2017.
The most interesting by far, though, are the ones the government categorizes as "unknown interference" or "insufficient information." Reading the information that is posted, it is not hard to imagine either a sloppy technician allowing their equipment to emit interference, or some sort of malicious actor with a jammer.
The site includes a number of reports from the Mediterranean and Middle East, which are never any surprise. US military commanders have called the area the most contested electronic warfare environment in the world.
A significant number of reports suggest persistent interference due to a device fixed in one
place.
A persistent problem in Edmonton, Canada, that has been going on for quite some time.
In Lancaster, CA a ... permanent disruption of GPS reception noticed over 6 months, driving daily in early evening and late evening, and is detected by 2 separate models of Garmin automotive GPS units. There is no overhead signage that could cause a drop out. The drop out and loss of reception covers a
span of approximately 200-300 yards centered on the Ave J overpass.
Boulder, CO reported ...Noticed irregular signal multiple times near the same block during weekdays.
From New Hampshire ...I have had a number of intermittent GPS issues within 1 mile of this location over the past year. GPS drops almost exactly 10 mph and the location plots diverge for approximately 1km parallel to the actual track. I took a picture of the GPS track showing the deviation. Contact me
(Dana) if you would like a copy of the track picture. I had previous similar incidents in the same vicinity.
In Puerto Rico ...My GPS position is changing. Beginning on 1-14-2020 almost every day, why is that? I measure from the same point at my home.
There are also quite a few that could well be due to a mobile source, possibly someone with a "personal jammer":
Driving in San Francisco and across the Golden Gate bridge with ...a 1,000 foot offset to the west.
A US Coast Guard vessel in Atlantic Beach, FL reported ...losing both of the ship's GPS receivers during their mooring evolution. Unit verified with another USCG vessel, at the pier, who was experiencing the same issue. Unit restarted both GPS displays with no resolve. After waiting approximately 20 minutes GPS signal regained and seems to be working properly.
In Warrenville, IL I used GPS for a trip immediately prior to this anomaly, without issue. When I attempted to enter my next trip leg, I noted an anomaly. My GPS apps could not locate my vehicle correctly and could not plot a course to my destination. The map display spun around multiple times, and at times placed my vehicle at the end of nearby dead end roads and even in the middle of a nearby field. I restarted the apps, to no avail. I restarted my phone and the bizarre behavior continued. About fifteen minutes after first noting the problem, I restarted my phone again and my GPS apps began working correctly. I do not know if it was a device issue or a GPS system issue. As of this date, I have used GPS twice on this device, without issue.
A user in Medford, OR lost their whole network for a while. We use GPS timing servers across our network within the CONUS. Across our network at approximately the same time, the timing servers went into holdover. As this issue was seen in multiple places, we do not think there were any issues with the hardware or software. We are trying to understand if something impacted the GPS satellite systems ability to provide timing on March 16th, 2020. (there wasn't)
Near Dulles Airport in VA I was on Rt. 50 heading East near Avion Pkwy close to Dulles Airport. The GPS navigation in my vehicle stopped working. When I looked for more information in the GPS it displayed no bars for a GPS satellite signal. This outage continued until the end of my trip in Reston, VA. I made two attempts to turn off my vehicle and restart the navigation during the trip, but this did not work to restart my GPS navigation. It was when I stopped the vehicle, stopped the engine, and got out of my car for 10-15 minutes that the GPS system resumed activity.
Rehoboth, MA - Position shown on maps was off by approximately
0.5 mile to the west. Also had same occurrence last night while in the same general area. When I noticed the issue on my Nav radio, I checked location on my iPhone and it was consistent with the radio in showing the wrong location.
Gibsonton, FL - I was driving following my GPS when all of sudden it lost GPS signal on the highway. I checked my vehicles GPS also and it could not lock onto me. It finally returned after about 20 mins but something must have knocked it out.
Quite the collection of reports!
If you would like to check them out yourself, feel free to visit the US Coast Guard Navigation Center website at:
https://navcen.uscg.gov/?Do=GPSReportStatus
Applanix introduces OEM solution for direct geo-referencing of airborne sensor data - GPS World
Applanix Corporation, a Trimble Inc. company, introduced the Trimble AP+ Air OEM solution for direct georeferencing of airborne sensor data. Learn more about the solution, which enables users to produce maps and 3D models without using ground control points.
https://www.gpsworld.com/applanix-introduces-oem-solution-for-direct-georeferencing-of-airborne-sensor-data/
Teardown: Mini GPS Jammer:
Read, meditate and do not imitate.
It is scaring to realize how easy is to jam GNSS signals.
This is the reason why we need a resilient, worldwide, integrated PNT infrastructure.
https://hackaday.com/2020/09/08/teardown-mini-gps-jammer/
GPS World 30th Anniversary Timeline - GPS World:
GPS World’s 30th anniversary GNSS timeline provides highlights in both system and policy development and industry over the past three decades. Check it out now.
https://www.gpsworld.com/gps-world-30th-anniversary-timeline/
Downloads available for free for these wonderful historical posters.
Yup, we added the question mark to the headline. The Army's Mounted Alternative PNT System (MAPS) is certainly helping soldiers in challenging GPS environments, but it doesn't come close to what most would call an "alternative."
https://www.linkedin.com/pulse/army-award-contract-gps-alternative-end-september-c4isrnet-goward/?trackingId=xPCLBR8YdSvXRpaxm8sG8A%3D%3D
In the words of the Army program manager, MAPS 1 is helping with jamming and
MAPS 2 is helping with spoofing. Lots of interesting capability in the package, including the eventual ability to use M-Code. There are IMUs involved and some other tech as you will see in the article, but not really what most folks would call an "alternative."
We also take issue with the quote "... will ensue soldiers know where they are even if
GPS isn't working." We are going to bet that most soldiers would have a fair idea where they are regardless. This sounds like a power point sound bite in a budget brief (don't get us wrong - these kinds of programs should be much better funded).
The most interesting thing, with MAPS, in our opinion, is the C4ISR/EW Modular Open Suite of Standards, or
CMOSS. This seems to be one realization of the DOD PNT Strategy's "Modular Open Architecture System" CMOS (everyone has to have their own name and acronym). The high level concept (which we have long espoused) is:
The best way to ensure you have PNT is to use a lot of diverse sources
This means you need to have a robust architecture
There are lots of diverse sources around right now and more could be brought on line with existing mature technology
When new sources become available, sophisticated users ought to be able to access them fairly easily
So a part of the critical path is figuring out a way for users to be able to access as many diverse sources (existing and future) as they can. Hence the modular, open architecture approach. This is not a trivial problem (authentication, fusion of diverse senors, prioritizing and 'voting,' to name a few) but it is an essential
one..
Note - we also link to a second, related C4ISRNet article below.
https://www.c4isrnet.com/battlefield-tech/space/
https://www.c4isrnet.com/battlefield-tech/space/2020/09/14/army-to-award-contract-for-gps-alternative-by-end-of-september/
https://www.c4isrnet.com/battlefield-tech/2020/09/10/army-launching-new-pnt-modernization-office-and-open-innovation-lab/
Jens Hoxmark:
Solution provider for Mission Critical PNT, IoT and 5G Telecom Ctrl Cmd and
Trusted Precise Wireless Timing, TPWiT.
Dana, yes, I read "army" and thought of people in close contact with Terra Firma. Doing 500kts makes it lot more challenging to shop at the local bakery, for sure.
But I came to think of the presentation by Dr. Aaron Canciani at the US Space Based Advisory Board meeting back in December 2018, where he presented the very interesting concept of "Magnetic Navigation"
https://www.gps.gov/governance/advisory/meetings/2018-12/canciani.pdf
This has also been published in Inside GNSS 15th June 2020 https://insidegnss.com/183615-2/
It's a very promising concept in combination with inertial and compact atomic clocks to be an alternative for a system that can be applied for military application by looking at the presented results, either in relative or absolute mode.
Jens Hoxmark:
Solution provider for Mission Critical PNT, IoT and 5G Telecom Ctrl Cmd
and Trusted Precise Wireless Timing, TPWiT.
2d
The detection of natural variation of the magnetic field is also applied for seismic interpretation. Please check the information on the homepage of "Electromagnetic Geoservices" EMGS.
http://www.emgs.com/content/1511/MT-data-acquisition
"The MT signal is measured using the same seafloor receivers as used for a conventional
controlled source electromagnetic (CSEM) survey.
However, the MT (MagneTotelluric) signal strength depends on solar activity interacting with Earth’s magnetosphere. To ensure good data quality, the receivers are kept on the seafloor for several days, continuously measuring the natural variation of the electromagnetic fields.
Resistivity models from MT inversion images deep structures such as basement and delineates complex salt and volcanic structures."
So they actually make constructive use of the Solar Magnetospheric alterations, in close cooperation with various observatories like the one in
Tromsoe that is
continuously measuring the magnetic flux /field http://flux.phys.uit.no/Last24/Last24_tro2a.gif
So there is definitely a magnetic "landscape" out there, that can be applied for navigation, even at 500 knots with present technology in pattern-recognition and fuzzy logic.
Tom Kerr:
In the 1970's and perhaps even before, (under Project: LINEAR CHAIR) the U.S. Navy was investigating just that
above topic for external position fixes to compensate for deleterious gyro drift over time for U.S. submarines to avoid any "observables" exposure
(of antennas or sonar bathymetric map-matching to any potential enemy
surveillance). Such an endeavor was progressing back then and needed to utilize onboard Fluxgate magnetometers, which have recently greatly improved and reduced in size, as I learned at a recent 2018 series of
IEEE Boston lectures on Optics-related topics. In the mid 1970's, there was a Kalman filter design planned for magnetic position fix "navaid" update to a submarine-borne INS that was called a "Schmidt Filter". (Not corresponding to Stanley Schmidt nor to George Schmidt at
Draper Laboratory at that time, who were involved with novel use of Kalman filters of their own for navigation applications; but to another person named Schmidt.) For this approach to be useful, it was necessary for an accurate Earth's magnetic map to be available.
People had speculated on trying to marry magnetic navigation with Gravity-based maps of the Earth since there are unique features of each that may be complementary.
Specialized surface ship fleets would be needed to compile such maps of magnetic and gravity fields experienced at various depths.
GPS military code receives operational acceptance for early use - GPS World:
The Space and Missile Systems Center’s Production Corps achieved a major
GPS milestone with the approval for Operational Acceptance of GPS Military-Code
(M-Code) Early Use. Read more on the approval.
https://www.gpsworld.com/gps-military-code-receives-operational-acceptance-for-early-use/
Y. Jade Morton received the Johannes Kepler Award from the Institute of Navigation (ION).
Read about the advances she's made in receiver technology, automated data collection, robust carrier phase tracking and remote sensing.:
https://www.gpsworld.com/jade-morton-honored-with-ions-kepler-award/
https://www.keepgpsworking.com/
GPS World celebrates 30 Years of leadership (7 Oct. 2020):
https://www.gpsworld.com/four-decades-of-leadership/
What would the world do without GPS?
https://www.bbc.com/future/article/20201002-would-the-world-cope-without-gps-satellite-navigation
GPS Program Updates
and its role in the SMC Space Enterprise Architecture: as of 8 October 2020
GPS tracking devices industry to grow 12.2% CAGR by 2026:
According to a report by InForGrowth, the global GPS tracking devices market was valued at $1,567 million in 2018 and is expected to grow at a
CAGR of 12.2% during the forecast period 2026. Find out what factors are driving that growth.
https://www.gpsworld.com/gps-tracking-devices-industry-to-grow-12-2-cagr-by-2026/
Planes continue to fly into a GPS dark hole over the Mediterranean, puzzling experts:
https://fortune.com/tag/gps-2/
https://fortune.com/2020/11/01/planes-ships-gps-mediterranean-russia-syria-north-korea/
8 Examples of Artificial Intelligence in our Everyday Lives:
https://paper.li/The-Helen-Jackson-Daily#/
https://edgy.app/examples-of-artificial-intelligence
UK Getting National GNSS Disruption Monitoring System - GPS World:
https://www.gpsworld.com/cgi-to-develop-service-to-alert-uk-of-gnss-disruption/
GPS IIR/IIR-M satellite antenna patterns released for worldwide - GPS World:
Partnering with the U.S. Coast Guard Navigation Center (NAVCEN),
U.S. Space Force and Lockheed Martin Space have released the GPS IIR/IIR-M satellite antenna patterns for worldwide public use. Learn more about the resources. (Diagram: NAVCEN/Lockheed Martin) #GPS #satellite #antenna
https://www.gpsworld.com/gps-iir-iir-m-satellite-antenna-patterns-released-for-worldwide/
Justyna Redelkiewicz on how GSA is using Galileo to enable innovation:
This week, our colleague Justyna Redelkiewicz (Head of Section Consumer Solutions at the
GSA) sat down with Ronan Leonard from the Irish Tech News Podcast to talk about #Galileo, #IoT, and #EUSpace��️ enabling innovation and entrepreneurship.
You can listen to the podcast here: https://lnkd.in/dBGy75p
https://soundcloud.com/irish-tech-news/justyna-redelkiewicz-on-how-gsa-is-using-galileo-to-enable-innovation
https://www.gpsworld.com/directions-2021-galileo-expands-and-modernizes-global-pnt/
L5-only receiver designed for mobile phones:
GNSS receivers first reached the commercial domain in the early 1980s. Here's how receiver technology has advanced since then.
https://www.gpsworld.com/l5-only-receiver-designed-for-mobile-phones/
Safran Optics 1 Mission:
Delighted to be a part of the Safran Optics 1 team! See how our electro-optic and navigation systems solutions are making a difference in surveillance and reconnaissance missions for dismounted soldier, airborne, naval, and land vehicle operations.
https://lnkd.in/dqTaxTt
https://lnkd.in/deebVXG
GPS Dual Use:
https://www.linkedin.com/pulse/gnss-openess-two-edged-sword-jules-mcneff-gps-world-dana-a-goward/?trackingId=EhIdQKJPGGjjH51%2F8e5Yog%3D%3D
https://www.gpsworld.com/gps-and-gnss-confronting-dual-use-realities/
ESA seeks proposals to demo 5G positioning, timing - GPS World:
https://www.gpsworld.com/esa-seeks-proposals-to-demo-5g-positioning-timing/
High-Precision GNSS for Precision Agriculture & Farming:
With over 12 years of lean manufacturing experience, Hexagon | NovAtel provides excellent customer and technical support for #agriculture #OEM integrators.
See the broadest range of the highest precision #GNSS positioning products >> https://hxgn.biz/3fVtLgW
https://novatel.com/industries/agriculture
Coral reef conservation technology wins Copernicus Masters 2020 competition:
Reef Support, an automatic warning system that uses artificial intelligence and
satellite imagery to detect coral bleaching, algal blooms,
sediment plumes and debris caused by humans, won the Copernicus Masters 2020
competition. Learn more about the system and how it works. :
https://www.gpsworld.com/coral-reef-conservation-technology-wins-copernicus-masters-2020-competition/
ArcGIS web app incorporates datasets, NGS data layers for surveyors - GPS World:
Get an overview of an ArcGIS web application that incorporates various California-specific datasets and
National Geodetic Survey (NGS) data layers to assist surveyors planning vertical control surveys.
https://www.gpsworld.com/arcgis-web-app-incorporates-datasets-ngs-data-layers-for-surveyors/
We're launching the world's latest Earth-observing satellite to monitor sea levels & provide data for weather forecasting and climate
models:
5 things to know about Sentinel-6/Michael Freilich, a historic U.S.-European partnership:
https://lnkd.in/dX4cKEG
Our Buyers Guide has a dedicated site that we’re continuously updating to ensure that you have the most accurate and complete resource available. With 100+ product categories and new ones added regularly, the GPS World Buyers Guide (gpsworldbuyersguide.com) is the No. 1 resource when making purchasing decisions for your company. For more information on our guide or getting your company listed, please contact Emily Adkins at
eadkins@northcoastmedia.net.
OneWeb LEO PNT: Progress or Risky Gamble? - Inside GNSS:
https://www.linkedin.com/pulse/oneweb-leo-pnt-progress-risky-gamble-inside-gnss-dana-a-goward/?trackingId=IXglvqX%2BjdpkzNyzANh69A%3D%3D
https://insidegnss.com/oneweb-leo-pnt-progress-or-risky-gamble/
Under Attack – Receiver Response to Spoofing: Robustness vs. Resilience - Inside
GNSS:
https://www.linkedin.com/pulse/under-attack-receiver-response-spoofing-robustness-vs-dana-a-goward/?trackingId=0TZ8EdF5UIy5YNxd1QGmhA%3D%3D
https://www.ion.org/publications/browse.cfm
https://insidegnss.com/under-attack-receiver-response-to-spoofing-robustness-vs-resilience/
DHS PNT Conformance Framework - Important Step in "Toughening" Users:
Dana A. Goward's Blog Editor's Note: The community and government have long struggled to define "resilience" when it comes to
GPS/GNSS receivers. While it does not provide the "procurement language" so many have called for, this is a huge step forward for the community. We will likely publish more on this in the coming weeks, but we wanted to ensure it was highlighted for our readers.
https://www.dhs.gov/sites/default/files/publications/2020_12_resilient_pnt_conformance_framework.pdf
DoT Maritime Spoofing, Jamming Workshop Slides Posted:
https://www.linkedin.com/pulse/dot-maritime-spoofing-jamming-workshop-slides-posted-dana-a-goward/?trackingId=jZMcHijQjV55nsPUm%2BpPFQ%3D%3D
GRIT - GNSS Resilience and Integrity Technology:
It takes GRIT to protect your position, navigation and timing measurements. Introducing the new #GNSS Resilience and Integrity Technology
(GRIT), a commercial suite of firmware enabling trusted situational awareness and mitigation of possible interference and spoofing threats across applications and environments.
With spoofing detection, interference mitigation and time-tagged data snapshots of analog to digital samples to characterize your RF
environment,
GRIT protects your positioning solution no matter where it takes you.
Learn more >> https://hxgn.biz/32xOFhQ
Triton Submarines — famous for underwater explorations including that of the Titanic — replaced large, outdated computers onboard with rugged tablets.
Find out how the tablets have eased tracking and communication:
https://www.gpsworld.com/manufacturer-equips-submarines-with-rugged-tablets/
Solution to GPS Hacking:
To see unclassified commercial
document that discusses a solution to GPS Hacking as the first main article, please click this link.
Unmanned survey vessel efficiently maps seabeds - GPS World:
In the busy Shizuoka harbor, Weichao Liu of CHC Navigation used the company’s
Apache6 marine drone to take a bathymetric survey of a channel in preparation for dredging at a Shizuoka seaport. Here's how the survey was conducted.
https://www.gpsworld.com/unmanned-survey-vessel-efficiently-maps-seabeds/
GSA, Public Safety sign BroadGNSS agreement on critical infrastructure:
https://www.gpsworld.com/gsa-public-safety-sign-broadgnss-agreement-on-critical-infrastructure/
Europe seeks alternative PNT services, deadline Jan. 13 - GPS World:
https://www.gpsworld.com/europe-seeks-alternative-pnt-services-deadline-jan-13/
GNSS Access is the Mainstay of Modern World - Geospatial World:
https://www.gwprime.geospatialworld.net/interview/gnss-access-is-the-mainstay-of-modern-world/?utm_source=geospatial-world&utm_campaign=Box-1&utm_medium=prime-feature-box
South Korea partners with broadcaster on eLoran and 10-cm GPS - GPS World:
https://www.gpsworld.com/south-korea-partners-with-broadcaster-on-eloran-and-10-cm-gps/
Can I Trust These Signals? - Galileo's Proposed Authentication Services:
Dana Goward: "Authentication seems to be the challenge of the age. Can you trust information you find on line? What political "leaders" are saying? Or how about those signals from space?
The folks over at the EU's Galileo program are trying to do something about the signals from their satnav system, at least. They have plans for two authentication services. An open service available to all and a commercial, fee-based service.
Our colleague Logan Scott, of Logan Scott consulting (and one of the smartest guys we know) pointed out this blog post series
about these services. Our readers with a technical background will find it interesting.
And here is a presentation about them that was given at the PNT Advisory Board meeting last December.
We note that, while the US government likes to call GPS "the gold standard" for GNSS, no such authentication service is planned. The
USAF has been experimenting with Logan Scott's Chimera proposal, but we haven't seen any proposal to operationalize it.
All of these efforts are good, though they will require users to upgrade their recievers to take advantage. Even then, while
receivers would be more resistant to jamming and spoofing, they wouldn't be immune.
A system of systems apporach is needed, including terrestrial signals such as those mandated by the
National Timing Resilience and Security Act of 2018.
Let's get those on line too as quickly as possible, so users only have to upgrade their equipment once."
https://berthub.eu/articles/posts/galileos-authentication-algorithm-part-1/
(blog services)
https://www.gps.gov/governance/advisory/meetings/2019-11/pozzobon.pdf
(pdf presentation about them)
https://www.gpsworld.com/afrl-tests-chimera-to-battle-spoofers-and-hackers/
https://rntfnd.org/2018/12/06/sen-cruz-markey-cong-garamendis-statements-on-national-timing-security-resilience-act-signing/
3 Dec 2020 - U.S. DOT, MARAD Convene Panel on GPS Jamming and Spoofing - Maritime Executive:
https://www.maritime-executive.com/editorials/u-s-dot-marad-convene-panel-on-gps-jamming-and-spoofing
China Research Paper on Differential eLoran - Sensors Journal:
Research on the eLoran Differential Timing Method:
Abstract: An enhanced long-range navigation (eLoran) system was selected as the backup of
Global Navigation Satellite Systems (GNSS), and experts and scholars are committed to improving the accuracy of the
eLoran system such that its accuracy is close to the GNSS system. A differential method called
eLoran differential timing technology is applied to the eLoran system, which has been used in maritime applications of eLoran. In this study, an application of
eLoran differential timing technology in a terrestrial medium is carried out. Based on the
eLoran timing service error, the correlation of the timing service error is analyzed in theory quantitatively to obtain the range of the difference station in the ground. The results show that to satisfy the timing accuracy of 100 ns, the action range of
eLoran difference station on the land needs to be less than 55 km. Therefore, the
eLoran differential method is proposed, and in the difference station, the theoretical calculation is combined with the measurement of the signal delay to obtain the difference information, which is sent to the users to adjust the prediction delay and improve the
eLoran timing precision. The experiment was carried out in the Guan Zhong Plain, and the timing error of the user decreased from 394.7287 ns
(pre-difference) to 19.5890 ns (post-difference). The proposed method is found to effectively enhance the timing precision of the
eLoran system within the scope of action.
Please click this link to
see the unclassified pdf on eLoran Differential Timing Method
U.S. Already 0-1 in Tech War With China - National Defense:
Blog Editor's (Dana A. Goward) Note: A disturbing Op-Ed discussing China's dominance in rare earths and
progress on 5G, quickly suggesting that the score might already be 0-2. Or maybe 0-3
if you throw in AI.
However you are scoring, the U.S. is another point down to China in the tech war because of
PNT.
And it's not merely that Bei Dou is newer than GPS.
China has a Comprehensive PNT Plan announced at Stanford last year. And they are executing it. They have
PNT at MEO and are putting it at LEO and GEO. And they are
upgrading their Loran system to eLoran and expanding it into the less populated western region of the country. This for the express purpose of ensuring they have
PNT independent of space and terrestrial location.
https://www.nationaldefensemagazine.org/articles/2020/11/11/us-already-0-1-in-tech-war-with-china#:~:text=Chinese%20President%20Xi%20Jinping%20told,hot%20one%20with%20any%20country.%E2%80%9D&text=The%20U.S.%20record%20in%20this,%2C%20or%20possibly%200%2D2.
James Keissling, Systems architect and analyst: Commenting on recent late
2020 test intercept of potential enemy ICBM:
If you define a 'test' as having some representation of the underlying problem - then nope. Please consider the physical geometry of a real engagement - its effectively nose-on. As the shown diagram appears to be more a chase, its not clearly representative.
Ralph Savelsberg, Associate Professor at Netherlands Defense Academy:
I agree. One of the challenging aspects of intercepting an ICBM-like target is the larger closing velocity than when intercepting an IRBM. Assuming that the range at which the KV resolves its target doesn't change much, that leaves it with much less time to correct its trajectory and consequently it may run into the limit of its divert. So, if you want to reduce that risk you have to reduce the closing velocity and this is pretty much the geometry you'd pick for that. In the real world, however, it seems highly unlikely that you'd actually have this option.
Also see:
Video: https://youtu.be/5nsafpZv5SM
Russian and Chinese space weapons could plunge West into DARK AGES with crashed economy and mass blackouts, experts warn - The Sun:
Dana A. Goward's Blog Editor's Note: The Sun is a British tabloid known for its sensational take on most things. Sensationalism aside, we need to ask ourselves, what in this article is not true or likely true?
Debbie White, author
17 Dec 2020, 12:48
Updated: 17 Dec 2020, 15:05
RUSSIAN and Chinese space weapons could "unleash havoc" in a satellite attack which could cost the
UK some £1billion a day, experts have warned.
It is feared an orbital onslaught could shut down hospitals, crash the economy, knock out communications, and cause mass blackouts.
Space tech is becoming a new arms race as nations roll out anti-satellite
weapons, ground-based lasers and GPS jammers which experts say all pose a
"significant threat" to the West.
Leading boffins painted a bleak picture to The Sun Online of a devastating attack involving these devices which have stepped from the pages of science fiction.
The warning comes as the US and UK yesterday accused Russia of launching another anti-satellite missile -
the third of its kind in 2020.
And it follows China staking its claim to the stars by planting a flag on the moon as a spy chief warned: the Communist regime is the "greatest threat" facing the
UK.
https://www.thesun.co.uk/news/13344900/russia-china-space-weapons-crash-economy/
Galileo 6 Hour Outage 14 December - Update Posted
Dana A. Goward's Blog Editor's Note: We greatly admire the Galileo
project, all they have achieved and are still achieving. As a civilian project focused on economic and public benefits, the system has been designed with features not available in older and military systems such as GPS and GLONASS.
Building and operating a GNSS is an incredibly difficult and complex task, involving many difficult and complex sub-tasks. For example, we just had a conversation with Dr. Marc Weiss yesterday about the many subtleties and difficulties of building an atomic clock (not to mention one that needs to go into space), which is just one component of a
GNSS. You also need rocket science, Einstein's general AND special theories of relativity, and a whole lot more.
Very glad to see Galileo up and running again.
GPS and GLONASS have have outages also. Bei Dou's turn will come. Good reminders that no human-created system is perfect. All are subject to a host of vulnerabilities and threats.
The Galileo system was returned to its nominal state a few hours after the incident which occurred between 00:00 and 06:00 on Monday morning 14
December 2020.
This service incident is still under investigation. It is confirmed to be related to an abnormal
behavior of a ground atomic clock in the time determination function of the system.
The time synchronisation and orbit determination algorithms immediately flagged the data as MARGINAL (SISA*=NAPA**) before it affected the quality of the measurements.
However, the incorrect data was still uploaded to the satellites.
User receivers that do not process the health and status flags, or that keep MARGINAL satellites as part of the position solution computation, may have experienced large positioning errors.
* SISA: Signal In Space Accuracy
** NAPA: No Accuracy Prediction Available
*** Estimation provided based on rapid truth products available to date with the corresponding limitations.
Media note: This feature can be republished without charge provided the European
GNSS Agency (GSA) is acknowledged as the source at the top or the bottom of the story. You must request permission before you use any of the photographs on the site. If you republish, we would be grateful if you could link back to the
GSA website
(http://www.gsa.europa.eu).
https://www.gsc-europa.eu/news/further-information-on-the-event-of-14th-december
Jamming - It's not just for GPS anymore!:
It is the professional car thief's jammer toolkit! it jams GPS/GNSS, Wifi/Bluetooth/2.4 GHz, Key fobs, and Lojack. Jamming Wifi disables the
CCTV. It can also be used to stop a car from being unlocked or started near the scene of a crime. Even a police car.
(Jan. 2021) Blog Editor's (Dana A. Goward) Note: Admittedly, the below article has nothing to do with
GPS, GNSS, or navigation. But it does show a vulnerability of wireless technologies, especially those with weak signals.
And it adds to the overall national concern about resilience after we say so much far-flung damage to networks after the explosion outside an
AT&T office in Nashville.
That's why we advocate in "A Resilient National Timing Architecture" for a PNT resilience triad of
GNSS, fiber, and terrestrial low frequency, high power broadcasts. Three technologies that are as different from each other as possible.
BTW - we agree with the comment in the article - "It is not very sophisticated." Unfortunately, just about anybody can do this.
https://chicago.cbslocal.com/2021/01/04/thieves-jam-wireless-camera-devices-in-westchester-its-not-very-sophisticated/
Thomas Kerr III's comment on the above: We are aware that 5G
will be using phased array antennas, which can perform adaptive beam-steering
and null-steering to thwart certain types of jammers, so they can do more
with less power than before!
(Jan. 2021)Top 10 GPS Spoofing Events in History - Threat Technology:
https://www.linkedin.com/pulse/top-10-gps-spoofing-events-history-threat-dana-a-goward/?trackingId=kKUhaBCBI%2FSTTd7j9zD6gA%3D%3D
Blog Editor's (Dana A. Goward) Note: It is kind of jarring to realize that this has been going on
for so long that we can talk about "the history" of spoofing. One would have hoped that, given the potential dire implications, a serious effort to eliminate the problem would have mostly solved, or at least managed, it by now.
The above article is an interesting review. We are wondering if there were events even more interesting that would have made the top ten, but were never discovered or made public.
What would you have included in the list?
How about the Swiss auto show were the cars were spoofed to the UK and years into the future?
Or the time a military drone accidentally (we assume) spoofed a light aircraft over Los
Angeles?
How about when a passenger aircraft nearly crashed into a mountain?
Full disclosure, the author of the article below is employed by Regulus
Cyber, a corporate supporter of the RNT Foundation.
https://threat.technology/top-10-gps-spoofing-events-in-history/
(Jan. 2021) The new year is here and so are we — anytime you need our Buyers Guide, you can find it on its dedicated
site,
https://lnkd.in/eSK6qBs. And if your company is a
manufacturer, service provider or distributor and you are not listed or need to update your listing, please contact Emily Adkins at:
eadkins@northcoastmedia.net.
Solar Flux at New High, GPS Problems Possible - Space Weather News (29
November 2020):
Last year saw the sun reach solar minimum, the period of the least amount of activity (sunspots, flares, coronal mass ejections), We are now heading toward solar maximum.
"Coronal Mass Ejections (CMEs) are large expulsions of plasma and magnetic field from the Sun’s corona. They can eject billions of tons of coronal material and carry an embedded magnetic field (frozen in flux) that is stronger than the background solar wind interplanetary magnetic field (IMF) strength." (NASA)
Particularly strong CMEs impacting the earth can disable or damage satellites and ionize the
atmosphere preventing satellite signals from getting through.
The 1859 Carrington Event was so strong the "northern lights" were seen in the tropics and currents were induced in telegraph lines powerful enough to set some offices on fire. The same thing happened again in 1921 with the "New York Railway Storm," named after one of the offices that caught fire.
Earth narrowly missed being hit by a "solar super storm" in 2012.
Last week's forecast warned GPS users of potential problems, particularly in areas with auroras and in low latitudes, over the next week or so.
Thanks to Marco Lisi for highlighting this report for us.
GNSS reflectometry measurements improved with COVID-19 pandemic - GPS World:
A study shows the quality of GNSS reflectometry measurements may have improved significantly during the
COVID-19 pandemic with the lack of parked cars near the ground station. Learn more about the study, carried out by geodesists from the University of Bonn.
https://www.gpsworld.com/gnss-ro-measurements-improved-with-covid-19-pandemic/
(Jan. 2021) ESA-funded GIDAS helps protect critical systems - GPS World:
In late 2020, the first GNSS Interference Detection and Analysis System monitoring stations were installed at the Czech airport in Brno. Learn more about the system.
https://www.gpsworld.com/esa-funded-gidas-helps-protect-critical-systems/
Why Do We Need to Be Protecting Drone Operations from GPS Interference?:
https://www.commercialuavnews.com/security/protecting-drone-operations-from-gps-interference
FAA approves first fully-automated commercial drone flights - The Hill:
We hasten to point out that this FAA approval for BVLOS (beyond visual line of sight) operations comes with a wealth of restrictions on when and where these can take place. The restrictions will greatly reduce the chance of mishaps. And while the approval does not mention navigation or GPS, it does reference previous waivers that require not starting or ending operations if
GPS signals and equipment are not 100%.
That said, once operations are underway, GPS problems can arise that work against ending the flight and lead to an accident.
https://rntfnd.org/2020/07/20/gps-interference-crashed-a-survey-drone-in-the-uk-will-the-debate-resonate-in-the-us-c4isrnet-ligado/
https://thehill.com/policy/transportation/534552-faa-approves-first-fully-automated-commercial-drone-flights
Solar Flux Hits New High & Big Flares Possible Now
Space Weather News 11.26.2020
https://www.youtube.com/watch?v=L6L-FutZmw8&app=desktop
https://science.nasa.gov/science-news/science-at-nasa/2014/23jul_superstorm
https://www.nasaspaceflight.com/2020/08/carrington-event-warning/
http://www.solarstorms.org/SS1921.html
The Biggest Solar Flare In Years Was Just Seen, With More Coming Soon:
Thank God, the solar flare was not oriented directly toward the Earth. However, impacts on radio communications and on
GNSS signals are expected.
X-rays and UV radiation from the flare ionized the top of Earth’s atmosphere, producing a shortwave radio blackout over the South Atlantic….
Ham radio operators and mariners may have noticed strange propagation effects at frequencies
below 20 MHz, with some transmissions below 10 MHz completely extinguished.
https://www.forbes.com/sites/ericmack/2020/11/29/the-biggest-solar-flare-in-years-was-just-seen-with-more-coming-soon/?sh=1db939a17928
Our Sun Has Entered a New Cycle, And It Could Be One of The Strongest Ever Recorded:
By MICHELLE STARR8 DECEMBER 2020:
The Sun may be in for a very busy time. According to new predictions, the next maximum in its activity cycles could be the one of the strongest we've seen.
This is in direct contradiction to the official solar weather forecast from
NASA and the NOAA, but if it bears out, it could confirm a theory about solar activity cycles that scientists have been working on for years.
Much more below. Has good comments too!
https://www.sciencealert.com/the-new-sunspot-cycle-could-be-one-of-the-strongest-we-ve-ever-recorded
Belgian company Seafar pioneers barge automation technology:
SEAFAR integrated Septentrio’s AsteRx-U dual-antenna, multi-frequency, multi-constellation receivers into its autonomous vessels to provide sub-meter positioning for navigation and control. Get more details on this tech integration.
https://www.gpsworld.com/belgian-company-seafar-pioneers-barge-automation-technology/
Route Masters to build integrated public transport platform for African megacities - GPS World:
Route Masters signed up to the national SPRINT - SPace Research and
Innovation Network for Technology business support program to develop an innovative transport management solution for African cities. Learn more about the project.
https://www.gpsworld.com/route-masters-to-build-integrated-public-transport-platform-for-african-megacities/
Looking ahead to 2021, we want you to know that we are here for you anytime you need help making purchasing decisions for your company with our dedicated Buyers Guide site (https://lnkd.in/eSK6qBs), where you
can search for 250+ manufacturers/service providers, 100+ product/service categories, location and by keyword.
For more information on the above, please contact Emily Adkins at eadkins@northcoastmedia.net.
FlashbackFriday: 1976: This image features the first military GPS five-channel receiver built in one of several programs that studied the feasibility of
GPS. The receiver weighed more than 270 pounds and had seats for two operators!
Today, Raytheon Technologies completed the acquisition of Blue Canyon Technologies, a leading provider of small satellites and spacecraft systems components.
From sensing subsystems to mission systems integration and from launch and range support to on-orbit operations,
Blue Canyon will further our ability to develop space capabilities faster than ever.
Welcome to Raytheon Intelligence & Space, Blue Canyon. We look forward to working with you to deliver disruptive technologies to support our customers’ success in space.
http://rtxintel.co/3nH5yiu
James Taiclet on LinkedIn: Lockheed Martin is acquiring Aerojet
Rocketdyne. Learn more about
https://www.linkedin.com/posts/james-taiclet_lockheed-martin-is-acquiring-aerojet-rocketdyne-activity-6746570089086111744-Mmm9/?_lrsc=1446865f-64fa-44eb-b1c3-ae3ac25b1bb9
Boeing test sees five AI-enabled jets teamed up:
We've just flown five surrogate jets powered by our autonomous technologies at Australia’s newest commercial drone flight test range.
The ground-breaking mission system technology was developed with the support of over 90 personnel from small-to-medium enterprises and the Queensland Government as part of the
Advance Queensland project.
The technologies developed from the project will inform future autonomous aircraft. Watch the flight below!
https://www.flightglobal.com/defence/boeing-test-sees-five-ai-enabled-jets-teamed-up/141402.article
Erika Armstrong, 428,232 Aviation Enthusiasts | A "Chick" in the Cockpit
(her words, not mine) | ATP | Author | FRAeS | Keynote Speaker:
We've just flown five surrogate jets powered by our autonomous technologies at Australia’s newest commercial drone flight test range.
The ground-breaking mission system technology was developed with the support of over 90 personnel from small-to-medium enterprises and the Queensland Government as part of the
Advance Queensland project.
The technologies developed from the project will inform future autonomous aircraft. Watch the flight below!
#aviation #achickinthecockpit #pilots #pilottraining #pilotlife #E6B
GPS satellite SVN-77/GPS III SV04 set healthy for use - GPS World:
The U.S. Coast Guard Navigation Center has issued a notice that GPS satellite SVN-77 (PRN-14) was set healthy for initial use. Get more details.
https://www.gpsworld.com/gps-satellite-svn-77-gps-iii-sv04-set-healthy-for-use/
Joshua Cohen, Writer on national and international naval and defense issues:
The cheapest way to take out a carrier I know of:
1,900 crew of French aircraft carrier go into quarantine after Covid-19 outbreak!:
https://www.rfi.fr/en/france/20200412-1-900-crew-of-french-aircraft-carrier-go-into-quarantine-after-covid-19-outbreak
Congress hits fast-forward to field new capability to counter drones:
Congress wants to rapidly advance a joint program to develop and field a capability for countering drones, requiring the Pentagon to field a system as early as next fall and
adding more than $47 million to fuel the effort, according to the fiscal 2021 National Defense Authorization Act.
“The executive agent of the Joint Counter-Small Unmanned Aircraft Systems
(C-sUAS) Office, as designated by the Under Secretary of Defense for Acquisition and Sustainment, shall prioritize the objective of developing and executing a plan to develop, test, and begin production of a counter unmanned aircraft system that can be fielded as early as fiscal year 2021 to meet immediate operational needs in countering Group 1, 2 and 3 unmanned aircraft systems,” read the
NDAA language released 3 Dec. 2020.
GPS Jamming & Spoofing, 2020 Year in Review - Spirent's Guy Buesnel:
Blog Editor's (Dana A. Goward) Note: This is a repost of Guy's excellent article on Linkedin. We are reposting on all our social media to help distribute this interesting item as broadly as we can.
We found his three predictions for 2021 particularly interesting.
Our thanks to Guy for his on-going insights and excellet observations in this area.
Guy is a member of RNTF's International Advisory Committee.
Full disclosure - Guy's employer, Spirent, is a corporate supporter of the foundation.
Thousands of GNSS jamming and spoofing incidents reported in 2020.
Published on December 2, 2020.
Guy Buesnel
PNT Security Technologist - with expertise in testing system robustness against GPS Interference and spoofing threats
48 articles
Disruptions to GNSS signals have been rife throughout the year, caused by everything from embattled pig farmers to regional conflicts. Here are some of the most notable events of 2020.
2020 has been a remarkable year in many ways. But while the coronavirus pandemic has upended operations worldwide, some global trends have continued uninterrupted.
One of them is our increasing reliance on satellite positioning, navigation and timing
(PNT) services, now an integral part of everything from smartphones to driverless vehicles.
Another is the continued rise in instances of GNSS signal interference that put those services – and those who rely on them – at risk.
Thousands of disruption incidents have been reported throughout 2020, from China to California, and from the Arctic Circle to New Zealand. Here’s my roundup of the most significant events of the year, together with a few predictions for 2021:
December 2019: Intermittent GPS signal loss experienced by aircraft landing at
Harbin airport in north-eastern China is traced to a jammer installed at a nearby pig
farm.
The South China Morning Post reports that the jammer was meant to deter drones operated by criminal gangs, whose aim was to drop packets infected with swine fever on to the herd – forcing the farmers to sell the infected meat to them at lower prices.
An extraordinary story, and one that illustrates once again how the use of illegal jammers can have unintended – and potentially serious – consequences for civil aviation.
January: Mexico passes an anti-jammer law, having discovered that GPS jammers are
used in 85% of cargo vehicle thefts in the country.
The use of ‘personal privacy devices’ (small GPS jammers that plug into a vehicle’s cigarette
lighter) to aid cargo theft is so widespread that the Mexican government has made it illegal to manufacture, sell, buy, own, install or use PPDs in the
country.
In many countries today, only the use of such jammers is illegal – selling, buying and owning is
OK. But with criminal use of jammers on the rise, will we see similar laws passed elsewhere?
February: An alarming report made by a light aircraft pilot to NASA’s Aviation Safety Reporting System suggests possible
spoofing by a US Department of Defense (DoD) drone.
GPS World reports that the pilot noticed a DoD drone flying above them. At the same time, the aircraft’s
Primary Flight Display (PFD) started to show a location in Utah, and then
Montana, rather than its actual flight path to San Diego from Los
Angeles.
Even more worryingly, the aircraft’s primary navigation system did not recover after the drone encounter, eventually forcing the pilot to make a visual landing in San Diego. If there had been poor visibility that day, this could have been a dangerous incident for the pilot.
While it’s unclear whether this incident was due to incidental jamming or deliberate spoofing, the wake-up call here is the lack of resilience on the part of the navigation system. As radio frequency (RF) interference becomes increasingly common, systems need to be able to recognise when they are being disrupted, and to recover after the disruption has occurred.
February: In France, a manufacturer of high-precision GNSS equipment complains of regular disruptions to
GPS and Galileo signals at their factory.
The French Radio Frequency Agency (ANFR) investigates, and eventually tracks down the source of the interference… to a broadband router installed in the nearby apartment of an elderly lady. The defective router turns out to be emitting harmful interference centred on the 1581.15 MHz frequency, very close to
GPS L1 and Galileo E1 signals centered on 1575.42 MHz.
It’s a clear illustration of the threat of in-band and adjacent-band interference to GNSS-dependent systems, though I do wonder what the lady in question must have thought when a team of ANFR investigators with a directional antenna turned up at her door!
March: ‘Circle-style’ GPS spoofing is reported in Iran’s capital, Tehran. A
GPS user informs the US government that their (unspecified) device seems to be moving in a circle around the Iranian Army training college, when the device is in fact stationary.
GPS World follows up, finding that heatmaps from the Strava fitness app show the same circle pattern around the same building. It’s not the first time circle-style spoofing has been seen, but it’s the first outside of China, where similar patterns were observed in Shanghai in 2019.
The jury is still out as to what kind of spoofing equipment produces these circle effects (not to mention who’s doing it and why), but Spirent has had some limited success in attempting to replicate the effect in the lab, as this blog explains.
June: GPS jamming once again causes problems in the far north of Norway, close to the Russian border.
Local police have been reporting jamming incidents since 2017, affecting everything from ambulances to personal safety alarms. Norwegian authorities have identified Russia as the source of the jamming, but the attacks seem to be both unpredictable and unpreventable.
As Finnmark police chief Ellen Katrine Hætta told the High North News: “There is not much they can do about it. We as a society need to improve our systems." It’s a reminder that as civil reliance on GNSS grows, receivers must be protected against the effects of RF interference.
August: A drone crash in the UK highlights the safety risks posed by jamming and spoofing interference to
uncrewed aerial vehicles (UAVs).
The 25lb survey drone lost GPS reception due to RF interference at the survey
site. Although programmed to hover in place, it drifted with the wind, eventually crashing into a house and falling to the ground. Fortunately nobody was hurt, but serious injury could have resulted.
As drones are used for more tasks, manufacturers will need to ensure their receivers are robust and resilient, and that action taken by the drone on encountering
RF interference doesn’t have unintended consequences.
August: A fleet of Chinese fishing vessels are accused of misreporting their location to mask illegal fishing activity.
The ships were reporting a location off New Zealand via the Automatic Identification System
(AIS), an onboard system that reports a ship’s GPS co-ordinates. However, the Ecuador government said the ships were actually near the Galápagos Islands, where illegal fishing has occurred before.
This type of AIS ‘cloaking’ is just one of many ways that criminals use location spoofing of a
GPS-dependent system to aid their nefarious activities.
September: The US Maritime Administration (MARAD) renews its advice to the maritime industry to be vigilant for
GNSS disruptions worldwide.
It notes there have been multiple instances of interference in the Central and Eastern Mediterranean region, as well as the Persian Gulf and some Chinese ports, and encourages crews to report new instances to the US Coast Guard.
November: Echoing September’s MARAD warning, Fortune reports that GPS outages are now standard occurrences on commercial flight routes between the US, Europe and the Middle East.
Aviation association Eurocontrol says it received 3,500 reports of GPS disruption in
2019, an all-time high. Jamming is widespread across the central and Eastern Mediterranean, likely due to electronic warfare between conflicting factions in Syria, Libya and elsewhere in the region.
These reports are another reminder that RF interference is now commonly encountered in
geo-politically sensitive hotspots, creating major disruption for commercial shipping and aviation.
Three predictions for 2021:
The events of 2020 show that satellite-based PNT is becoming ever more central to our lives – and consequently, that countering the many threats to GNSS has never been more critical.
Having closely observed the evolution of GNSS threats over many years, I’d like to make three predictions for the year ahead:
#1 Spoofing will become a greater threat to commercial users
GNSS Spoofing (broadcasting of a fake or delayed GNSS signal) has been a concern in the defence domain for many years, but it’s now starting to impact commercial and civilian users too. As more devices and autonomous systems rely on GNSS, and as spoofing know-how and equipment are now relatively easy to acquire, we’ll see more unprotected systems fall victim to spoofing attacks.
#2 Assured PNT testing will move off the laboratory bench and into the field
From drones to driverless cars, autonomous systems need assured PNT services to operate reliably. Manufacturers will need to assess the real-world performance, reliability and resilience of multi-sensor systems to check they’re functioning adequately for both safety- and liability-critical operations. For that reason, we’ll see performance and integrity testing of platforms expand from the laboratory and into the field.
#3 PNT vulnerabilities will be integrated into cybersecurity frameworks
Historically, GNSS receivers have been developed and tested as standalone systems. But today they’re increasingly one subsystem in a complex device with multiple ports, sensors and connections. To a hacker, the RF interface is just another attack vector, which means that increasingly, we are likely to see that the specific
GNSS vulnerabilities in the RF domain are dealt with as part of an integrated cybersecurity framework, rather than treated in isolation.
Stay up to date with GNSS vulnerabilities.
Threats to GPS/GNSS are evolving all the time. To stay up to date with the latest news, events and incidents, join over 1,300 industry professionals in the
GNSS Vulnerabilities LinkedIn group.
https://www.linkedin.com/pulse/gps-jamming-spoofing-2020-year-review-spirents-guy-buesnel-goward/?trackingId=EGo3%2FCi4SmwRfKVQBSIAuQ%3D%3D
A pertinent comment by Allan Bradly: https://www.linkedin.com/posts/allan-bradley-59b0093a_trumpadministration-activity-6741050405935046656-Y-wx
GPS Backup Finally Moving Closer - Aviation News from the Reason Foundation:
https://www.linkedin.com/pulse/gps-backup-finally-moving-closer-aviation-news-from-dana-a-goward/?trackingId=7GQ8F8qF%2FhffKDU%2By%2Fq4EQ%3D%3D
https://reason.org/aviation-policy-news/tsa-quiet-skies-program-critiqued-again/#e
Google to improve urban GPS accuracy for apps:
The wrong-side-of-the-street position error in smartphones is caused by reflected GPS signals in
cities (due to multipath of a particular GPS satellite signal to the receiver of
essentially the same intensity so it isn't easily weeded out and distinguished
from the primary signal), and Google employees embarked on an ambitious project to help solve this problem. Hear from
Frank van Diggelen, principal engineer, and Jennifer Wang, product manager,
Google, on how the team has worked to resolve this issue in Androids.
https://www.gpsworld.com/google-to-improve-urban-gps-accuracy-for-apps/
LDACS-NAV could guide global aviation:
GNSS is a critical single point of failure for navigation in the aviation industry. A new white paper published by Egis says it’s time for the industry to get rid of legacy navigation aids and catch up technologically with the rest of the communications industry.
https://www.gpsworld.com/ldacs-nav-could-guide-global-aviation/
GPS is Major Threat Vector in US Maritime Cyber Plan:
The National Maritime Cybersecurity Plan issued on the 2nd of December and recently made available joins a list of national strategies and plans addressing security for the
95% of all U.S. trade that depends on maritime. It outlines a number of challenges and threats the nation must address. None are trivial.
Challenges include a too-small workforce, confused federal-level governance, and information/intelligence sharing. Also, a highly varied set of commercial and other governmental stakeholders, many of which might find it difficult to establish a credible cybersecurity program.
Threats are many and varied to both Information Technology (IT), and
Operational Technology (OT) systems. A category of threat is described as coming through electromagnetic spectrum system (EMS). Threats via EMS include communications systems and GPS.
At one point the plan describes how, in 2016, the Department of Homeland Security predicted that loss of
GPS signals would bring port operations to a halt if a backup system wasn't available. This wasn't a difficult prediction because the U.S. Coast Guard had already seen it happen in 2014.
Elsewhere the plan describes jamming and spoofing navigation as significant problems. Also, how 14 maritime groups petitioned the
U.S. Coast Guard Commandant to raise the issue at the International Maritime Organization (IMO). GNSS interference was later described by IMO as an urgent and safety of life issue.
It is good to see another national document including GPS disruption as a cyber issue. This is appropriate as disruptions:
Interfere with IT and OT systems' ability to communicate;
Interfere with end use devices (computers and equipment of all kinds) and Can insert false data into systems;
Find the plan here: NATIONAL MARITIME CYBERSECURITY PLAN, TO THE NATIONAL STRATEGY FOR MARITIME SECURITY.
(Jan. 2021) New Appointee for Key National PNT Post:
President Biden has appointed Professor Robert Hampshire from the University of Michigan as Principal Deputy Assistant Secretary for Research and Technology at the U.S.
Department of Transportation (DOT).
DOT is the federal lead for civil positioning, navigation, and
timing (PNT) issues. Within the department, the Assistant Secretary for Research and Technology has this responsibility. This makes Professor Hampshire a critical player in national
PNT community.
Here is a link to the University of Michigan's announcement about the appointment that includes a link to
Prof. Robert Hampshire's bio:
https://news.umich.edu/u-ms-robert-hampshire-joins-biden-administration-to-work-in-transportation-research-and-technology/?fbclid=IwAR0ti2G00-gcbuyJN-9f6IOrxnZRnnNI65tt7ebAWgh2al5bEus_1tYVmbY
HP names 3 new C-suite members — a chief technical officer, a chief legal officer and a chief strategy and incubation officer - Silicon Valley Business Journal:
https://www.bizjournals.com/sanjose/news/2021/01/19/hp-names-three-new-c-suite-execs.html
Harvey Anderson, Esq. (Tom Kerr's cousin's son!) was mentioned in the above news
article as now being the new Chief Legal officer at HP.
(Feb. 2021) Russian Electronic Warfare System Is Capable Of Neutralizing GPS, Galileo and BeiDou Systems - Sputnik International:
Blog Editor's (Dana A. Goward) Note: This article by Sputnik is interesting as it has some nuggets of information that haven't been widely known. For one, it reveals
their spoofing capability exists simultaneously in hundreds of locations. Earlier analysis of Russian spoofing operations concluded there were only a few sets of
equipment, and these were regularly relocated to follow VIP movements. We speculate
this was the case at the time (2016 - 2019 or so) and more equipment has since been
developed and deployed.
The article also says the system is called "Pole-21." This system, or one very like it,
has long been used to spoof navigation receivers in Moscow, the Black Sea and
elsewhere.
Electronic warfare has long been a focus for Russian forces. It is seen as
a way to neutralize the West's technology and turn it from an advantage into
a disadvantage.
As examples, years ago Russia announced installation of GPS jammers on cell towers to
disrupt cruise missile attacks on their homeland.
And a standing Russian boast has been that their electronic warfare capabilities
(which are VERY impressive) make Western aircraft carriers
useless.
It is always good to be reminded of Russia's impressive abilities to neutralize our essential space-based PNT services. Also, of the
West's critical vulnerability
relative to others Russia, China, South Korea, and
Saudi Arabia are NOT nearly as vulnerable. They each have sovereign,
terrestrial, high power, difficult-to-disrupt,
PNT systems for the express purpose of protecting themselves from interruptions of space-based signals.
MORE FROM ORIGINAL SOURCE:
Russian Electronic Warfare System IS Capable Of Neutralizing GPS, Galileo and
BeiDou Systems
Sputnik International News
1 February 2021
Siberia and the Ural Mountains region will receive Pole-21 radio-electronic warfare systems designed to
defend against drones and other weapons. In this way, the
Pole-21 will become an impediment to satellite navigation systems, drones, allowing
to avoid possible attacks by cruise missiles and weapons of high precision.
In addition to interfering with enemy communications, the system is also able to inject false coordinates into these communications in order
to disorient the opponent.
According to the Russian Ministry of Defense, Izvestia told the portal, the systems
will be installed in the Ural Mountains and Siberia later this year.
Unlike systems of the same type, the Pole-21 has hundreds of radio interference transmitters installed at
a considerable distance from each other. Each of the transmitters
can be controlled remotely, allowing electronic defense to operate over an area of hundreds of square kilometers.
Although the technical characteristics of the equipment are kept secret, it is
known that the export version is capable of neutralizing the GPS satellite navigation
systems, of North American origin, European Galileo and Chinese BeiDou.
The area of action of a complex can reach 150 km². A single station on the
Pole-21 is sufficient to interfere with communications from a GPS receiver over a distance
of up to 25 km. The global GPS positioning system is used, in addition to smartphones, also in military drones, and high-precision weapons.
In addition to being able to interrupt the enemy's satellite communications, the
Pole-21 system also allows transmitting wrong coordinates to the opponent's
technological platforms. It is known that the Pole-21 entered service in
2016, having already been used in the Eastern Military District of Russia and at the
country's 201st Base in Tajikistan.
Note: We are not able to provide a hyperlink to the original of this article. The text above
was received from a highly trusted source and we are confident in its
accuracy. It is also entirely consistent with other Russian press releases and announcements.
(Feb. 2021) This image features Gladys West, whose work helped develop the Global Positioning System. Learn more about her career in a March 2018 GPS World article:
https://www.gpsworld.com/how-gladys-west-uncovered-the-hidden-figures-of-gps/
(Feb. 2021) Army researchers detect broadest frequencies ever with quantum receiver:
A new quantum sensor can analyze the full spectrum of radio frequency and real-world
signals, unleashing new potentials for Soldier communications, spectrum awareness
and electronic warfare. U.S. Army researchers built the quantum sensor, which
can sample the radio-frequency spectrum—from zero frequency up to 20
GHz—and detect AM and FM
radio, Bluetooth, Wi-Fi and other communication signals:
https://www.army.mil/article/242980/army_researchers_detect_broadest_frequencies_ever_with_quantum_receiver
(Feb. 2021) Sewage Plant Jams GPS Around Airport - AVWeb:
Blog Editor's (Dana A. Goward) Note: This problem impacted aircraft within 25 miles of the Wilmington, NC airport and had been documented since May 2020.
This long standing problem was finally resolved due to the persistence of the airport 's highly dedicated pilots association. They worked with the
Airline Pilots Association, the Aircraft Owners and
Pilots Association, the National Business Aviation Association, their local congressman, the
Federal Aviation Administration, and the Federal Communications Commission to find the
source of the problem.
After several attempts over the course of three months, the FCC and the FAA finally located the problem as coming from the local sewage treatment plant.
Good thing it wasn't a bad guy trying to not get caught.
Wireless Utility Controls Jammed GPS Near Airport:
by Russ Niles
January 31, 2021
Pilots using Wilmington Airport in North Carolina are hoping the mysterious and
random interruptions in GPS service near the airport are a thing of the past after an
FAA team tracked down
the likely cause. The agency officials discovered signals coming from
a utility company’s wireless control system were jamming GPS within a
two-mile radius of the airport. Pilots had
reported losing the signal in critical phases of flight including instrument
approaches. The situation was serious enough that it prompted a 25-NM NOTAM around the airport warning pilots
that they could lose GPS.
Authorities shut down 85 “emitters” used by the system within two miles of the airport and the outages stopped, according to the
ILM Pilots Association newsletter.
https://www.avweb.com/aviation-news/sewage-plant-wireless-controls-fouled-airport-gps/
(Feb. 2021) ‘It’s a safety issue.’ Questions raised about GPS-based landing systems at US airports following 7 Investigators' report - WXYZ:
Blog Editor's (Dana A. Goward) Note: In the1990's after the advent of GPS, the FAA planned to decommission its ground-based navigation aids and have aircraft rely entirely on space-based systems,
essentially GPS and its augments. In 2001 a Volpe Transportation Systems Center report showed what a horribly bad idea that is.
It also pointed out that it would be a bad idea for other parts of society to rely just on GPS for navigation and
timing.
Aviation authorities in the the US and Europe, though, have never completely moved away from that
idea. "Wouldn't it be great if we could get rid of those expensive ground-based systems," they think,"
and just use those incredibly expensive satellite systems, that are paid for by someone
else!" So the
ground-based aviation navigation beacon network continues to shrink and age. We understand the
FAA has dozens of new VOR equipment in storage, for example, that they
have no funds or plans to
install (wouldn't you include the install funds with the purchase
budget?).
And while some other nations are using new, much more capable and safer Instrument Landing Systems that could increase the safety, flow, and efficiency of major airports dramatically, we understand
no efforts are underway to install them in the U.S.
https://www.wxyz.com/news/local-news/investigations/its-a-safety-issue-questions-raised-about-gps-based-landing-systems-at-us-airports-following-7-investigators-report
Report on Navy Laser, Railgun and Gun-Launched Guided Projectiles:
https://news.usni.org/2021/01/13/report-on-navy-laser-railgun-and-gun-launched-guided-projectiles-7?fbclid=IwAR1cZU3yX6McKpcaPp83LDY-qVQ9888hBs2exIaev_bczoEUwxjGrklI5n0
(Jan. 2021) Why Do We Need to Be Protecting Drone Operations from GPS Interference?:
Awesome article by Danielle Gagne at CommercialUAVNews (Commercial UAV Expo ) about our
[infiniDome LTD (GPSDOME)] work with Easy Aerial Inc. creating a new
resilient drone standard for #bvlos #borderpatrol #uavs #jamming
https://www.commercialuavnews.com/security/protecting-drone-operations-from-gps-interference
(Jan. 2021) FAA Files Reveal a Surprising Threat to Airline Safety: the U.S. Military's GPS Tests - IEEE Spectrum:
Blog Editor's (Dana A. Goward) Note: Perhaps the title of this article should have been "GPS Jamming Set to Crash Passenger Aircraft."
One thing I learned in Aviation Safety Officer school is that aircraft accidents are not random. If you are paying attention, you can almost always see the indications and warnings well
in advance. A host of minor problems, then some close calls.
More close calls (called in aviation "near misses"), and then finally, an aircraft is lost and people die.
The problem is that human beings often have difficulty acting to prevent bad things from happening. And for those who try to head off accidents, it is usually difficult to persuade others
that the time, effort, and expense is necessary.
Until after a bunch of people are dead. Then it is often a bit easier. But not always.
We knew natural gas leaks were dangerous. But nothing was done to give it an odor until the New London, Texas school exploded. 295 children had to die before we took action.
We knew passengers in automobiles were dying because they were not restrained in crashes. Tens of thousands had to die before we had seat belts and mandatory use.
We knew hardened cockpit doors would help prevent aircraft hijackings. 2,977 people had to die on 9/11 in a direct attack on the nation before better doors were installed.
We know GPS signals are vulnerable and need to be integrated with stronger terrestrial signals. How many will have to die before we do that?
https://spectrum.ieee.org/aerospace/aviation/faa-files-reveal-a-surprising-threat-to-airline-safety-the-us-militarys-gps-tests
(Jan. 2021) America Has a GPS Problem - New York Times:
https://www.linkedin.com/pulse/america-has-gps-problem-new-york-times-dana-a-goward/?trackingId=Njw0Q3fvf51fgaWgPTMmGA%3D%3D
Blog Editor's (Dana A. Goward) Note: Great opinion piece by Kate Murphy of the NY Times. Not much new in here for our regular readers, but very good to see this in such a well
respected and widely read outlet.
Note that she says the RNT Foundation "...advocates for an eLoran backup of
GPS." We also advocate for all the other systems the government has said are needed to backup GPS.
The government has most recently said that a combination of fiber, UHF beacons, and Low Frequency (a la eLoran) is needed to make America safe. We are happy to and do advocate for that.
Our strongest advocacy is for the government to take action. So far, all we have seen (1) studies that focus solely on critical infrastructure, and (2) warnings to users to protect themselves.
Kate Murphy, a frequent contributor to The New York Times, is a commercial pilot and author of “You’re Not Listening: What You’re Missing and Why It Matters.”
Jan. 23, 2021, 11:00 a.m. ET
Time was when nobody knew, or even cared, exactly what time it was. The movement of the sun, phases of the moon and changing seasons were sufficient indicators.
But since the Industrial Revolution, we’ve become increasingly dependent on knowing the time, and with increasing accuracy.
Not only does the time tell us when to sleep, wake, eat, work and play; it tells automated systems when to execute financial transactions, bounce data between cellular towers and throttle
power on the electrical grid.
Coordinated Universal Time, or U.T.C., the global reference for timekeeping, is beamed down to us from extremely precise atomic clocks aboard
Global Positioning System (GPS) satellites.
The time it takes for GPS signals to reach receivers is also used to calculate location for air, land and sea navigation.
Owned and operated by the U.S. government, GPS is likely the least recognized, and least appreciated, part of our critical infrastructure. Indeed, most of our critical infrastructure would
cease to function without it.
The problem is that GPS signals are incredibly weak, due to the distance they have to travel from space, making them subject to interference and vulnerable to jamming and what is known
as spoofing, in which another signal is passed off by hacking as the original. And the satellites themselves could easily be taken out by hurtling space junk or the sun coughing up a fireball.
As intentional and unintentional GPS disruptions, respectively, are on the rise, experts warn that our
over reliance on the technology is courting disaster, but they are divided on what to do
about it.
https://www.nytimes.com/2021/01/23/opinion/gps-vulnerable-alternatives-navigation-critical-infrastructure.html
(Jan. 2021) Robots emerge from stealth: Locata's PNT orbs provide port guidance - GPS World:
GPS World visited with officials at the Ports of Auckland, New Zealand and the Australian company
Locata to reveal a revolutionary port automation system.
Find out how this system could change the way containers are handled around the
globe:
https://www.gpsworld.com/robots-emerge-from-stealth-locatas-pnt-orbs-provide-port-guidance/
(Jan. 2021) US R&D Plan for Resilient PNT - At the very last minute:
https://www.linkedin.com/pulse/us-rd-plan-resilient-pnt-very-last-minute-dana-a-goward/?trackingId=9Reit8UgULMxNBR0QCgqdQ%3D%3D
One hour and fourteen minutes before its end, the Trump administration published the
"National Research and Development Plan for PNT Resilience."
Does it matter? Many of those who authored it are no longer in a position to do anything about it.
But yes, it still matters for several reasons. First, R&D in any area, is almost always a good thing. Also, the folks who developed the plan provided a very nice
outline of the many ways we need to improve our understanding of our PNT services. Also why and how they should be improved.
And a lot of the smart folks who contributed to it are still important players in the national
PNT space.
Many see the last administration as preferring to continue admiring the problem rather than acting to solve it. "More study" was a relatively constant call
as a way of deflecting the need for action.
But this is an R&D Plan. On its own, for what it is, it's a pretty great
document.
We (i.e., Dana A. Goward) will likely write more about this in the coming weeks.
In the meanwhile, since the electronic archives at the White House are undergoing a transformation from the old administration to the new, you can find a copy
of the plan on our website at the link below.
https://rntfnd.org/wp-content/uploads/NSTC_Position_Navigation_Timing_RD_Plan_Jan2021.pdf
(Jan. 2021) DOT report: L-band, UHF, LF and fiber PNT needed to protect US - GPS World:
January 19, 2021 - By Dana Goward
In a long-anticipated report issued last week, the Department of Transportation
(DOT) outlined the results of its GPS Backup Technology Demonstration
project.
As officials had previously projected, it called for a system-of-systems approach using multiple complementary technologies.
The report called for an architecture that included signals from space in the L band, terrestrial broadcasts in the
Ultra High Frequency (UHF) and Low Frequency
(LF)
spectra, and a fiber backbone to synchronize and feed precise time to terrestrial transmitters.
The demonstration project and report were mandated by Congress in legislation passed in late 2017 and funded in early
2018.
Delays within the administration resulted in the project beginning in early
2019.
...
Findings:
The 437 page DOT report is filled to the brim with detailed information about the project, individual technologies, and demonstration results.
The Executive Summary says that...in addition to the findings from the DHS December 2018 effort (which, as mentioned above, don’t seem
to be publicly available),
the DOT demonstration had four key findings:
All TRL-qualified vendors offered showed PNT “performance of value” and one
showed value in all scenarios.
Neither eLoran company succeeded in the Static Basement Timing scenario.
R-Mode ranging did not meet the minimum technical readiness level (TRL) of 6.
Deployment effort and coverage (infrastructure per unit area) are significant cost
factors.
Addressing the needs of critical infrastructure owners and operators, the report concluded
the needed “…technologies are LF and UHF terrestrial and L-band satellite broadcasts for
PNT functions with
supporting fiber optic time services to transmitters/control segments.”
https://www.linkedin.com/pulse/dot-report-l-band-uhf-lf-fiber-pnt-needed-protect-us-dana-a-goward/?trackingId=95m51YyL0Hs4i5FgToBEnA%3D%3D
https://www.gpsworld.com/dot-report-l-band-uhf-lf-and-fiber-pnt-needed-to-protect-us/
https://www.transportation.gov/administrations/assistant-secretary-research-and-technology/complementary-pnt-and-gps-backup
NOAA Contract for Prototype GPS-Denied Receiver:
Blog Editor's (Dana A. Goward) Note: We were interested to see this navigation sensor fusion effort sponsored by
NOAA.
According to Jack Elston at Black Swift, the $400K contract will result in a prototype navigation receiver that will probably fly first on one of the company's drones.
Integrating other sources with GPS as a way of increasing resilience will likely be a burgeoning field.
The US Department of Defense is pursuing the holy grail of this with it's modular open systems approach (MOSA). The idea is to be able to integrate, prioritize, and
use virtually all legacy and future P, N, and T sources with a simple "plug and play" box or algorithm.
Rather than re-describe Black Swift Technologies' project, we have reproduced their press release below.
18 Jan. 2021, NOAA Awards Black Swift Technologies Contract to Develop GPS-Denied Navigation
Posted at 14:34h in Uncategorized by Michael Irvin
Enabling Beyond Visual Line-of-Sight (BVLOS) Operations for
UAS in GNSS-Denied Environments
Boulder, CO – (January 18, 2021) – With nearly 95,000 miles of domestic coastline,
NOAA’s National Geodetic Survey faces a daunting task. Under current
FAA
regulations, unmanned aircraft system (UAS) operators are required to keep their aircraft within visual line of sight, making coastline surveys time-consuming and
arduous, having to tediously map 2-mile segments at a time, and then relocate to the next operating area. To address this challenge
NOAA has selected Black Swift
Technologies (BST) to develop commercially viable technology enabling GPS-denied navigation of UAS—technology critical in enabling long distance,
beyond visual
line-of-sight (BVLOS) flights.
“Enabling BVLOS operations in the National Airspace System is largely an issue of improved sensing,” states Jack Elston, Ph.D., CEO of
Black Swift Technologies.
“Operators, both government and commercial, are looking to perform missions over longer distances. These users represent a number of currently under-utilized
applications for UAS due to capability and regulations—applications such as aerial imaging, environmental observation, precision agriculture, and infrastructure
monitoring and inspection.”
Accurate aircraft position information is essential for safe UAS operations within the
Unmanned Aircraft Systems Traffic Management (UTM) system. Unfortunately, the
primary system that provides position information, GPS is a single point of failure in the system, subject to jamming and spoofing, along with on-board failure or poor
signal quality in locations such as urban canyons, at high latitudes or at high altitudes.
BST aims to provide a robust, secondary navigation option through their diverse-source
global positioning system (DS-GPS) that will provide accurate position updates
to UAS in GPS denied areas through augmented sensor suites and advanced machine learning capabilities. This will be performed through the careful weighted fusion
of advanced machine vision algorithms with the localization of the vehicle using triangulated signals of opportunity—essentially everything emitted within a set of frequencies
from a non-moving source.
How it Works:
DS-GPS utilizes a standard GPS receiver augmented through the use of additional sensing capabilities to estimate inertial velocity and absolute position. This information
allows for the vehicle to determine when the GPS signal is degraded either through spoofing or environmental effects. Other sensors, including cameras and a
software-defined-radio, can then be used to replace the
GPS as the primary navigational sensor providing position and velocity estimates from diverse sources.
“Black Swift Technologies has worked with NOAA in particular in the past to supply systems that can be used for both coastline work and atmospheric science,”
Elston emphasizes. “The work in this
SBIR is a natural extension of the machine learning based techniques BST has been developing for unmanned aircraft. One
of the key technologies of this work is to use machine vision (both optical flow and
SLAM) to allow continued safe flight of UAS in the event of loss of
GPS. Work
associated with coastline inspection and mapping would greatly benefit from BVLOS operations since this would significantly reduce the amount of time an operator
has to spend in the field.”
https://bst.aero/noaa-awards-black-swift-technologies-contract-to-develop-gps-denied-navigation/
(Jan. 2021) The drive to autonomy: Companies gear up with sensors, strategies - GPS World:
For the past decade, widespread deployment of autonomous vehicles
(AV) has been just over the horizon. Check out some challenges car manufacturers are facing
with AV development
https://www.gpsworld.com/the-drive-to-autonomy-companies-gear-up-with-sensors-strategies/
(Jan. 2021) US Army heads into future tactical unmanned aircraft rodeo next month:
The U.S. Army is heading into a culminating event used to evaluate four different unmanned aircraft systems capable of replacing the service’s current tactical
UAS —
the Textron-made Shadow.The service will hold a “rodeo” at Fort Benning,
Georgia, the last week of February through the first week of March where all five of the
Brigade Combat Teams which spent the last year evaluating Future Tactical UAS systems will be represented, Brig. Gen. Wally Rugen, who is in charge of Army
aviation modernization, told Defense News in a recent interview.
The Army selected four UAS in 2019 as candidates to replace the Shadow. Each candidate would undergo soldier assessments to help inform requirements for
a FTUAS capability that would fit into a future vertical lift ecosystem to include new helicopters and other air-launched effects.
The service first selected two teams to provide systems for the soldier-led evaluation in March 2019:
Martin's UAV and Textron’s AAI Corporation.
Martin UAV
teamed with Northrop Grumman to provide its V-Bat UAS. Textron offered its
Aerosonde HQ.
(Jan. 2021) Norway Diplomacy Plan for GNSS Disruption Not Working:
The report was completed on the 19th of December 2019. With the speed of government, it was reviewed, approved and finally posted for public viewing on the
18th of December 2020:
https://www.regjeringen.no/no/dokumenter/gnssgps-disruptions-in-aviation/id2815123/
Titled "GNSS/GPS Disruptions in Aviation," the report by a Norwegian working group also offers some familiar comments on the essentiality of
GNSS/GPS,
as well as a number of insights into Norwegian and European thinking and plans for transportation.
It repeatedly discusses the criticality and vulnerability of GNSS services:
It has gradually been recognized that GNSS systems are vulnerable, with a high risk of serious consequences for society in the event of a signal outage...
A serious failure in the PNT services will spread to other parts of society and may cause problems in maintaining services on which the population depends.
PNT system failures can occur for reasons including disruption of GNSS signals.
The report also documents how, despite this, the west is becoming increasingly dependent on
GNSS. For example:
Despite the development in disruptions of GPS signals in aviation, the EU continues to
emphasize the use of satellite-based systems in all modernization and
digitalization in aviation in the years to come. (EC IR 1048/2018)
Norway, especially Norwegian aviation in the far north, is particularly dependent upon
GNSS. Despite its findings, the report offers surprisingly little in terms of
proposed action other than continued monitoring and diplomacy.
In fact, it declares that diplomacy with Russia is the solution.
Russia repeatedly jammed GPS in northern Norway for years, including during NATO's 2018 Trident Juncture
exercise. In February 2019 Norwegian officials
held a diplomatic meeting with the Russian military to protest and discuss the matter. The jamming then stopped. This led the report to say:
Since this meeting and until the finalization of this report on 19 December 2019,
no GPS disruptions have been registered in Norwegian airspace over
Finnmark county. If, contrary to expectation, similar problems should occur in the future, this experience shows that we have both military and diplomatic
communication channels available that permit such problems to be addressed.
Unfortunately, shortly after the report was completed, GPS in northern Norway was being jammed again.
(Jan. 2021) Allan Klo 19 April 2020:
Powerless against GPS interference:
Once again, jamming of GPS signals has created challenges for civil aviation in eastern Finnmark. The Norwegian authorities have repeatedly addressed
the problems of the alleged culprits – Russia – without helping.
Despite this jamming, Norway's group of State Secretaries approved the report as it was on the 6th of May 2020.
Political Context
The Norwegian government is in a politically tight spot on this. As a staunch member of the European Space Agency, Norway's leaders have
devoted tens of millions of dollars to the Galileo GNSS project.
And in 2015, to show loyalty to the Galileo effort, they shut down the nation's Loran
system. This despite warnings from internal security experts
about GNSS vulnerability, increasing jamming and spoofing, and the desirability of maintaining sovereign, exceptionally
difficult-to- disrupt PNT.
Norwegian officials also ignored observations that Russia was keeping its Loran system to use alongside satellite systems, and pleas from
the UK to keep some of the Norwegian stations on line to enable its new precision e-Loran network.
Perhaps the actions of Norway's politicians were to be expected. After all, the United States had shut down its Loran system in 2010 to show
loyalty to GPS. - Don't you hate it when the U.S. sets a bad example that gets others in trouble?
Yet Norway has some advantages over the U.S. in this regard.
Norway is even more dependent on GPS/GNSS than America. And Norway has a neighbor that regularly reminds them of GNSS vulnerability, and that
they can take the signals away with the flip of the switch. And, by the way, even if Norway were interested in doing the same thing to Russia,
it wouldn't have nearly the same effect because of the Russian Loran system.
We hope these things will eventually stir Norwegian leaders from their lethargy and set them on the path to establishing a terrestrial PNT system
of their own.
Perhaps it will be an eLoran system like the one South Korea is
building. South Korea's system will cooperate and work with neighboring Russian Loran
to provide users greater coverage and resilience. The Korean system will also be able to operate on its own and protect the nation during those times
when
Russia and other neighbors are not in a good mood:
https://www.regjeringen.no/contentassets/21b7b9ae14714d67999bcd8c75211996/disruptions-in-aviation.pdf
(Jan. 2021) Greece and France ink $3 billion contract for Rafale fighter jets:
The Greek and French defense ministers in Athens today witnessed the signature of the contract to buy 18 Rafale fighter aircraft after Greek parliamentarians
approved the €2.5 billion ($3.04 billion) deal earlier this month.
Nikos Panagiotopoulos and his French counterpart, Florence Parly, looked on whilst Theodoros Lagios, the director general of armaments and investments at
the Greek Ministry of Defense, and Eric Trappier, chairman and CEO of Dassault Aviation, the aircraft manufacturer, signed the contract for 12 second-hand aircraft,
which will be taken out of the French Air Force inventory, and six new ones.
The contract includes the aircraft’s weapons. A second contract was signed for the logistical support of the aircraft.
Speaking after the signing ceremony, Parly remarked how pleased she was that Greece had made a “resolutely European choice” by opting for the French-made
aircraft, thus becoming Dassault’s first European export customer.
(Jan. 2021) Our team delivered the first F/A-18 Super Hornet from our Service Life Modification line in San Antonio to the US
Navy:
This marks our second SLM line upgrading and extending the life of Super Hornets to ensure readiness for the U.S.
Navy.
(Jan. 2021) FAA Files Reveal a Surprising Threat to Airline Safety: the U.S. Military's GPS Tests - IEEE Spectrum:
Blog Editor's (Dana A. Goward) Note: Perhaps the title of this article should have been "GPS Jamming Set to Crash Passenger Aircraft."
One thing I learned in Aviation Safety Officer school is that aircraft accidents are not random. If you are paying attention, you can almost always see the indications
and warnings well in advance. A host of minor problems, then some close calls. More close calls
(within aviation, called "near misses"), and then finally, an aircraft is lost
and people die.
The problem is that human beings often have difficulty acting to prevent bad things from happening. And for those who try to head off accidents, it is usually difficult to persuade others that the time, effort, and expense is necessary.
Until after a bunch of people are dead. Then it is often a bit easier. But not always.
We knew natural gas leaks were dangerous. But nothing was done to give it an odor until the New London, Texas school exploded. 295 children had to die before we
took action.
We knew passengers in automobiles were dying because they were not restrained in crashes. Tens of thousands had to die before we had seat belts and their
mandatory use.
We knew hardened cockpit doors would help prevent aircraft hijackings. 2,977 people had to die on
9/11 in a direct attack on the nation before better doors
were installed.
We know GPS signals are vulnerable and need to be integrated with stronger terrestrial signals. How many will have to die before we do that?
(Jan. 2021) FAA Files Reveal a Surprising Threat to Airline Safety: the U.S. Military's GPS Tests:
Military tests that jam and spoof GPS signals are an accident waiting to happen
By Mark Harris
Early one morning last May, a commercial airliner was approaching El Paso International Airport, in West Texas, when a warning popped up in the cockpit:
“GPS Position Lost.” The pilot contacted the airline’s operations center and received a report that the U.S. Army’s White Sands Missile Range, in South
Central New Mexico, was disrupting the GPS signal. “We knew then that it was
not an aircraft GPS fault,” the pilot wrote later.
The pilot missed an approach on one runway due to high winds, then came around to try again. “We were forced to Runway 04 with a predawn landing with
no access to [an instrument landing] with vertical guidance,” the pilot wrote. “Runway 04…has a high
CFIT threat due to the climbing terrain in the local area.”
CFIT stands for “controlled flight into terrain,” and it is exactly as serious as it sounds.
https://spectrum.ieee.org/aerospace/aviation/faa-files-reveal-a-surprising-threat-to-airline-safety-the-us-militarys-gps-tests
(Jan. 2021) Rheinmetall and MBDA win contract for Naval Laser Weapons System - Naval News:
https://www.navalnews.com/naval-news/2021/01/rheinmetall-and-mbda-win-contract-for-naval-laser-weapons-system/
(Jan. 2021) After more than five years of hard work by 131 authors from 18
countries, the new book set Position, Navigation, and Timing
Technologies in the 21st Century (PNT21) is finally ready to meet readers. Here's what you can expect to see in the book.:
https://www.gpsworld.com/new-2-book-set-explores-21st-century-pnt/
(Jan. 2021) Use of autonomous vehicles in mining and farming touted at CES 2021 - GPS World:
At this year’s virtual CES 2021 trade show, Caterpillar
Inc. and John Deere showcased autonomous machines that are being used worldwide in farming and mining projects.
Check out the innovations both companies brought to the table.
https://www.gpsworld.com/use-of-autonomous-vehicles-in-mining-and-farming-touted-at-ces-2021/
University revises PNT backgrounder In response to concerns - GPS World:
January 26, 2021 - By Dana Goward
George Mason University has revised a briefing paper on positioning,
navigation and timing (PNT) in response to concerns about its accuracy.
The university’s National Security Institute “NSI Backgrounder — Beyond
GPS: The Frontier of Positioning, Navigation, and Timing Services” was first issued on Dec. 2. Some staff
on Capitol Hill and members of industry soon had concerns about several of its assertions.
https://nationalsecurity.gmu.edu/bgpsfb/
Responding to letters from industry in the above active link, National Security Institute
(NSI) Executive Director and Professor Jamil Jaffer said he determined that three of the issues raised, while not fatal to
the document, warranted clarification.
eLoran callout: The first was a statement in the backgrounder that the National
Timing Resilience and Security Act (NTRSA) “specifies
13 technical requirements for a GPS backup,
which essentially define the eLoran system.”
This was a concern to some on the hill as Congress is generally reluctant to specify solutions. Legislators prefer to specify outcomes and then defer to the executive branch on how to
make them happen.
Members of industry pointed out that government systems like WWVB and the low-frequency portion of
DARPA’s STOIC program:
https://www.darpa.mil/program/spatial-temporal-and-orientation-information-in-contested-environments,
as well as commercial systems like NextNav and Locata, could meet or be adapted to meet the
existing NTRSA requirement.
The revised backgrounder says the NTRSA “specifies 13 mainly technical requirements for a
GPS back-up, which align closely with the capabilities of the eLoran system. Other systems
may meet the Act’s requirements to varying degrees.”
Multiple technologies. The revised backgrounder also corrects a statement that the
NTRSA requires the Department of Transportation to establish an eLoran system. It now says
“a system that complies with the Act, and DOT may pursue multiple technologies in implementing the Act.”
Department officials had previously said they were taking a system-of-systems approach and expected to employ multiple technologies. Subsequently, a
DOT report was released that
documents the need for several diverse systems. It lists transmissions using
low frequency: (eLoran, STOIC), ultra high frequency:
(NextNav, Locata) and L-band: from space:
(GPS, Satelles).
It also says the terrestrial transmitters should be interconnected by
fiber.
Public-private partnership: A third correction was made in the document to reflect how the
Congressional Budget Office regarded the possibility of using a public-private partnership
in previously proposed legislation.
Members of industry also expressed concern that one of the authors of the document serves on the advisory board for Satelles Inc. and that this was not disclosed in the paper.
https://www.satellesinc.com/national-security-institute-policy-paper-calls-for-pnt-diversity/
The backgrounder appeared on the Satelles website the same day it was
published.
The university concluded that such disclosure was not necessary as the paper said the author “provides advisory services to industry, including in the
PNT area.” At the author’s request,
though, his profile on NSI’s webpage will be updated to show his relationship with
Satelles..
(Jan. 2021) Memorandum on Space Policy Directive 7 | The White House:
It looks like data and signal authentication is going to be made available for civil
GPS users. This is basically what Chimera is all about on NTS-3.
From Memorandum on Space Policy Directive 7 (https://lnkd.in/eza-AGA)
"Secretary of Defense and the Secretary of Homeland Security,
jointly develop and validate requirements and a funding strategy to implement data and signal authentication
of civil GPS and wide area augmentations for homeland security and public safety purposes consistent with the Federal
Radionavigation Plan or its successor plan."
(Jan. 2021) What to do when GPS is compromised:
https://www.raytheonintelligenceandspace.com/news/feature/what-do-if-gps-compromised
(Jan. 2021) James Litton, GPS and precision ag pioneer, dies:
By Dana Goward
January 26, 2021
James D. Litton, GPS pioneer and founder of NavCom Technology
Inc., died over the weekend at his home in California with his family at his side. He was
89 years old.
Litton was an early contributor to the development of GPS user equipment. He also played a pivotal role in the
GPS-driven transformation of global agriculture that has greatly benefited humanity.
No alt text provided for this image
Litton was the director of engineering at Magnavox Research Labs when researchers were working on using
CDMA for range measurements, a precursor to the GPS system. He also worked on the original proposal for GPS Phase I.
Later, as general manager of Magnavox’s Marine and Survey Systems Division, he helped develop new and advanced commercial navigation and survey receivers for both the Navy’s TRANSIT system and the Air Force’s GPS.
His team developed the first microprocessor-based commercial satellite navigation receivers and the first commercial
GPS survey software. This led to Magnavox eventually having more than a 90 percent share of the survey receiver market.
The firm eventually held more than two dozen patents for improvements in GPS
technology.
In 1992, Litton left Magnavox to start a consulting business. Two years later,
with Ron Hatch, K.T. Woo and Jalal Alisobhani, he founded
NavCom Technology Inc. With Litton as CEO, NavCom became a significant player in the GPS
marketplace.
Among its achievements was development — under contract — of a single-frequency WAAS-capable GPS aircraft navigation
receiver.
NavCom also began a relationship with Deere & Company, supporting more efficient and productive agriculture. This relationship was so successful that
Deere purchased NavCom in 1999. Litton continued to lead the company and serve as part of
Deere’s senior management team for eight more years.
In recognition of his many achievements to the field, Jim Litton was presented the Institute of Navigation’s Hays Award in
2006.
Among his many contributions, his impact on global agriculture might well have been his greatest, according to
Brad Parkinson, the original chief architect for GPS.
“His work transformed agriculture into a data-driven, technological industry that was incredibly more efficient,” Parkinson said. “The cost savings and increases in productivity have impacted billions around the world.”
With challenges related to the COVID-19 pandemic, Litton’s family are still considering arrangements for a memorial service. Information will be posted on the
RNT Foundation website when it becomes available.
Jim's family has created a memorial fund at Doctors Without Borders for those wishing to make a donation in honor of his life and many good works. Click Here.
https://www.gpsworld.com/james-litton-gps-and-precision-ag-pioneer-dies/
(Jan. 2021) AutoX, an Alibaba Group backed startup announced it had rolled out fully driverless
robo-taxis on public roads in Shenzhen.
(Jan. 2021) Passwordless: The Future of Authentication:
Eliminate reliance on passwords. Download the free white paper to discover the five-step path to
passwordless authentication.
https://duo.com/resources/ebooks/passwordless-the-future-of-authentication?
(Jan. 2021) Loh’s Method: A Different Way to Solve Quadratic Equations:
https://mathladyhazel.medium.com/lohs-method-a-different-way-to-solve-quadratic-equations-bc585281c166
In the latest episode of Visual Studio Toolbox, #ASPNET PM Sayed Hashimi shows us how to create and optimize .NET Core project
templates.
Learn more: https://msft.it/6045plHlx
From the skies to the stars:
From propellers to propulsion, #RaytheonTech is engineering the advanced aerospace and defense technology that connects humanity to the skies and the stars.
Learn how: https://lnkd.in/durmTMU
(Jan. 2021) What is space debris and why is it a potential problem? Join us on
10th February 2021: “Space Debris Day”, at 1:00PM for a live Zoom
webinar to learn about the science and politics involved in solving this astroenvironmental issue, and why it is important
for us to better manage what we leave out in space. https://lnkd.in/gtNgfBF
Why the risk of space collisions is skyrocketing now
See https://youtu.be/ZKKIAsQ-cww
The OpFires countdown has begun. We're (i.e., RTX) partnering with DARPA to demonstrate the capability of a hypersonic boost glide missile that blazes through
air defenses to engage targets at medium ranges. Read more: http://lmt.co/2XyFECe
DARPA’s Operational Fires (OpFires) program awards a new phase of the intermediate-range hypersonic ground-launch weapons program to
@LockheedMartin.
It involves full-scale missile fabrication, assembly, and flight testing. https://lnkd.in/gPga3-P
(Jan. 2021) Mitochondrial Changes Key to Health Problems in Space:
Living in space isn't easy. There are notable impacts on the biology of living things in the harsh environment of space. A team of scientists has now identified a possible
underlying driver of these impacts: the powerhouse of the cell, called mitochondria, experiences changes in activity during spaceflight. Recently published in the journal
Cell, these results used data collected over decades of experimental research on the
International Space Station, including samples from 59 astronauts. Studies such
as these are critical to understanding the effects of low gravity, radiation, confined spaces, and more as
NASA sends astronauts deep into space for extended missions
to the Moon, Mars, and beyond.
https://www.nasa.gov/feature/ames/mitochondria-cell-science
'LEO is an orbital junkyard' NASA - The Tragedy of the Commons & Losing Access to Space:
"LEO is an orbital space junk yard. There are millions of pieces of space junk flying in
LEO. Most orbital debris comprises human-generated objects, such as pieces of space craft,
tiny flecks of paint from a spacecraft, parts of rockets, satellites that are no longer working, or explosions of objects in orbit flying around in space at high speeds.
Most “space junk” is moving very fast and can reach speeds of 18,000 miles per hour, almost seven times faster than a bullet. Due to the rate of speed and volume of
debris in LEO, current and future space-based services, explorations, and operations pose a safety risk to people and property in space and on Earth." - NASA Headquarters Library
Some estimates have over 100,000,000 objects in Low Earth Orbit (LEO) large enough and moving fast enough to damage satellites and other objects.
Such collisions create more debris, which then creates more opportunities for collisions... You get the idea.
It is called the Kessler Syndrome and was featured in the film "Gravity" with Sandra Bullock and George Clooney. In the film, a Kessler event takes out the
International Space Station. Spoiler alert, Clooney eventually dies and Bullock barely makes it back to
Earth (but her hair stays miraculously intact).
Some percieve a slower but developing Kessler Event happening even now.
Debris was first blamed for damage to a satellite in 1981 (even more so from an
F-15 in the late 1980's). Reports have continued since. These have included multiple instances of damage
to the
International Space Station, space shuttles, as well as satellites. We were unable to find an authoritative compilation of these events (Dear Readers, please send if you know of one),
but it is a sure bet they are getting more, rather than less, frequent.
Space, especially LEO space, is suffering from The Tragedy of the Commons. Much like the world's oceans, cyberspace, and fresh air, many use and degrade it for their own profit, but few (if any)
take care of and preserve it. Short term greed and a disregard for the common good - perhaps two sides of the same coin - override the long term interests of all.
Here are some short videos on the problem that may be of interest. The most pessimistic envisions humanity trapped on Earth by a
LEO layer of debris too thick to even risk flying through.
Eyes on the Sky - University of Texas - A UT space video that does not feature Todd Humphreys, for some reason.
Space Debris - A journey to Earth - by the European Space Agency (ESA).
ESA regularly holds conferences on this subject.
The End of Space - by Kurzgesagt a German educational animation studio.
Note: The risk to GPS/GNSS satellites at MEO is much less because there is, probably, much less debris. The only known case of
MEO pollution was in 1963 when the U.S. Air Force
at the behest of MIT Lincoln Laboratory, deployed 480 copper needles for Project West Ford, an attempt to create an artificial
ionosphere to bounce radio waves off of for communications
in case of a terrestrial or atmospheric nuclear event. NASA believes most of the needles have de-orbited by now.
All of this is not to say there aren't efforts to restore and preserve LEO.
ESA plans to have a space debris collector launched in 2025. And there are
multilateral international agreements
about the need for future satellites to automatically deorbit at the end of their useful lives. This is essential - tens of thousands
of new satellites are planned for LEO in the next couple of years.
Yet Russia and China continue to practice destroying satellites in space. And most of the existing debris, including the millions of lethal bits too small to be tracked, aren't going away anytime soon.
One wonders if efforts to make the problem better will ever be able to get ahead of natural and human effects that steadily make it worse.
Perhaps, one of the things we should do is ensure every service from space is also provided independently from the ground. That way, regardless of a Kessler Event, Carrington-like solar flare,
or some other mishap to one or more space-based services, we won't be caught unprepared.
It is possible to see the future sometimes. You just have to be brave enough to not avert your eyes.
The above editorial authored by Dana A. Goward (and tampered with here
and there by Tom Kerr)
https://www.linkedin.com/pulse/loe-orbital-junkyard-nasa-tragedy-commons-losing-access-goward/?trackingId=JVp1MfUye8foof7A6X5Nzw%3D%3D
(please see Dana A. Goward's original on Linkedin since many topics have active links
supplied there that Dana A. Goward did not convey here)
First Fix: National timing architecture needed now:
December 14, 2020 - By Dana Goward
The Empire State Building sits atop a massive and solid foundation that hardly anyone ever sees. Above ground it has 2.8 million square feet of offices and hundreds of businesses. It houses 15,000 workers. Yet it would all come crashing down if the underlying and unseen foundation weren’t incredibly strong and dependable.
Timing is the unseen foundation of every networked technology, digital broadcast, financial transaction, electrical grid management and of most navigation systems, just to name a few applications. Yet, as GPS World readers know, signals from our dominant source of timing — GPS — are very faint and easily disrupted.
Short term, localized disruptions happen all the time, and many systems have adapted. A delivery driver using a jammer to hide from his boss is unlikely to disrupt a cell base station as he passes by, for example.
But more serious threats are out there. More and more hobbyists are finding ways to spoof receivers. Every few decades the sun flares strongly enough to fry satellites or charge the ionosphere. And because there are so few alternatives, GPS and other GNSS have become huge, tempting targets for adversary nations, terrorists, and sophisticated hackers.
Instead of Manhattan bedrock, our timing foundation is sometimes more like shifting sands.
Systems engineering tells us that, if something is essential, there ought to be two, three or more independent ways of receiving it. Most aircraft, for example, have two or three systems powering the flight controls —
because controlled flight is important!
The white paper “A Resilient National Timing Architecture” outlines how the United States can leverage existing infrastructure and provide all citizens two, and many of them three, independent paths to
Coordinated Universal Time (UTC).
It proposes a national timing back- bone of mature technologies with very different failure modes —
GNSS, eLoran and fiber. This combination will provide rock-solid timing at the 500 ns or better level of accuracy relative to UTC everywhere across the nation, and at 100 ns or better in major metro areas. Users accessing two or more systems would be nearly bulletproof to
attempted timing service disruptions.
The National Timing Resilience and Security Act of 2018 mandated a terrestrial system to back up
GPS timing. Our white paper provides a path forward.
Complying with the law while benefiting current and future technologies should be sufficient motivation. If it isn’t, we must also realize that not acting on this will continue to place us behind other nations such as the United Kingdom, South Korea, Russia and China — all of whom are actively reinforcing their national timing systems.
The task will not be a simple one. Yet America was able to overcome the expense and difficulties of building
GPS, at the time the world’s most refined and complex technology, and put it in space. By comparison, establishing a resilient national timing architecture using existing technology in our homeland would be child’s play.
Timing is essential. It is infrastructure for our infrastructure. If our national timing is weak,
so is everything that is built upon it.
We will profit from ensuring our timing is as strong, resilient, and easily accessed as possible.
And we will suffer if it is neglected.
https://www.gpsworld.com/first-fix-national-timing-architecture-needed-now/?utm_source=Navigate%21+Weekly+GNSS+News&utm_medium=Newsletter&utm_campaign=NCMCD201209002&oly_enc_id=9675F1206356D9T
Relevant Comment on the above:
Jeffrey DeCoux, Chairman - Autonomy Institute - leading Intelligent, and Autonomous Infrastructure & Systems. Path to Commerce for Industry 4.0 and Autonomous Systems
We have billions of dollars being allocated to invest in the nation's digital infrastructure that supports 5G/ITS/Edge/APNT/Grid. Resilient
APNT and electricity are coming.
https://youtu.be/9-w0G7sD8NQ
GPS III SV04 receives operational acceptance, 1 more needed for M-code:
The fourth GPS III satellite, space vehicle (SV) 04, received U.S. Space Force’s Operational Acceptance approval. Read more about this milestone.
https://www.gpsworld.com/gps-iii-sv04-receives-operational-acceptance-1-more-needed-for-m-code/
(Jan. 2021) High-performance gyroscope for automotive, aeronautic and industrial applications:
CEA-Leti scientists, together with researchers at Politecnico di
Milano, have developed the world’s first high-performance gyroscope for operating in severe environments, such as industrial and aeronautic equipment and automobiles.
According to the team, this breakthrough proves it is possible to detect minute rotational movement even among system vibrations.
https://www.newelectronics.co.uk/electronics-news/high-performance-gyroscope-for-automotive-aeronautic-and-industrial-applications/233988/
(Feb. 2021) Trimble introduces next-generation 3D paving control platform - GPS World:
Trimble Inc. released the Trimble Roadworks 3D Paving Control Platform, a next-generation platform for 3D asphalt paving control systems. Check out the platform's
features.
https://www.gpsworld.com/trimble-introduces-next-generation-3d-paving-control-platform/
(Feb. 2021) What if every satellite suddenly disappeared? - TED ED by Moriba Jah,
2 Feb 2021:
Blog Editor's (Dana A. Goward) Note: A great five minute video summary of all the bad things that happen when we don't have satellites. A lot of talk about
GPS, as you can imagine, and
the need for terrestrial backups for all our space systems.
Of course, in addition to the two disaster scenarios described, GPS signals could also fail due to human error (think the 2016 mishap), cyber attack, and electronic
warfare.
Dr. Moriba Jah has a distinguished background in the space sciences and is currently an Asst. Professor at the University of Texas, Austin.
https://www.youtube.com/watch?v=jVzbs81bDy0&feature=emb_title
(Feb. 2021) The DoT’s “Complementary PNT and GPS Backup Technologies Demonstration Report” released this January has some excellent data on the relative performances of various
systems in timing and positioning. Figures 130 and 131 of the report rank the systems on “performance sensitive” and “cost sensitive” bases respectively and has
received a lot of attention. While I don’t disagree with the general assessments, there is considerable hazard in applying them blindly to select a national strategy.
https://www.transportation.gov/sites/dot.gov/files/2021-01/FY%2718%20NDAA%20Section%201606%20DOT%20Report%20to%20Congress_Combinedv2_January%202021.pdf
The Gold Standard will be a "system of systems", not a particular system!
Firstly, there were several technologies NOT demonstrated, most notably 4G and
5G NR, both of which have significant (and demonstrated) timing and positioning capabilities
independent of GNSS. A second major hazard lies in deployed
availability. Until and unless a technology is fully deployed over the coverage area,
you will have holes
in coverage! The market will play a major role in deciding what will actually be available. A third consideration is
domain applicability. The report partially addresses
this in having diverse test environments ---indoor/outdoor; stationary/moving;
etc. but it does not make an assessment as to whether or not the technology is applicable for a
given class of user. Fiber optic to the cell phone may NOT
be as cool as it sounds.
Finally, there is the question of resiliency. NONE of the technologies
was tested in an adversarial environment, e.g. jamming, cyber-attack,
etc. A truly resilient
system is a "system of systems" and the measure of its resilience is
performance under attack and that is mostly a function of how well the systems are
integrated.
In closing, this is an excellent report well worth reading that provides some good guidance on several technologies that
could help in establishing resilient
augmentations. Some ( e.g., Satelles / LEO Iridium) are available now for a
subscription price. Others (e.g., NexNav/928 MHz Beacons) perform
extremely well but
will require significant infrastructure investment as contrasted with (UrsaNav /
eLoran) which provides lesser positioning capabilities but can be deployed fairly
inexpensively. Ultimately, the choices will be made by the market!
(Feb. 2021) Detect and Avoid (DAA) Requirements Explained:
New today: "Detect and Avoid Requirements Explained According to Airspace and ACAS Classifications." Understand how your mission will determine whether your flights will operate under UTM or ATC, require #RemoteID or #ADSB, and what a certifiable #DAA system will look like.
http://ow.ly/74Hj50Dm3B7
The above prompted a comment from
James Farrell (Owner at Vergil):
Again, avoidance can NEVER succeed in dense traffic without accounting for fundamentals:
1) instantaneous position history won't tell what's ahead,
2) transponder distance is good; cross-range is CRUDE,
3) cross-range is improved by sightline rotation,
4) that happens ONLY at dangerously CLOSE range,
4) that forces last-moment desperation climb/dive,
5) knowledge of dynamics will be increasingly essential!
For more on the above topic, also see: https://youtu.be/84De8EM8S0U
(Feb. 2021) Calls Grow to Find Back Up Systems for GPS - National Defense:
Blog Editor's Note - There are lots of reasons to worry about GPS vulnerability and our over-reliance on it.
Disruptions can lead to accidents (like the near crash of a passenger plane in 2019), a halt to farming operations and digital broadcasts, and severe impacts to
telecommunications. Just to name a few.
Perhaps our biggest concern should be more existential. A major solar event or other mishap
could halt GPS services for days, or even permanently. What then?
It could make the COVID-19 pandemic look like a mere warm-up act.
Calls Grow to Find Back Up Systems for GPS:
2/11/2021
By Nick Adde
Five years ago, the Iranian navy seized and temporarily held the crew of two U.S. Navy gunboats that had entered Iranian waters. Though the 10 sailors were
eventually released, the photos of them kneeling on the deck of an Iranian vessel with their hands behind their heads was a national embarrassment at the least,
and a potential trigger for a more serious confrontation at worst.
Then in 2019, President Donald Trump came close to calling for an airstrike against Iran in retaliation for shooting down a Navy RQ-4 Global Hawk drone
over the Strait of Hormuz.
Though much about both incidents remains classified, at least one expert believes that they occurred because Iran was able to interfere with the Navy crafts’
GPS,
causing them to move off their planned course and into hostile territory.
The incidents point to the vulnerability of global navigation satellite systems, and those operated by the U.S. in particular, said
Dana A. Goward, president of the
Alexandria, Virginia-based Resilient Navigation and Timing Foundation, a nonprofit organization dedicated to promoting resiliency in such systems.
The earlier incident was supposed to be “an easy trip down the coast of Saudi Arabia, from one port to another,” said Goward, a retired Coast Guard captain who
served as director of the service’s Marine Transportation System.
“Somehow they ended up way to the left, where the Iranian navy just happened to be waiting for them,” he said.
Likewise, the Global Hawk was flying near the Iranian coast but still in international airspace.
“All of a sudden it’s taking a right-hand turn toward Iran, and getting shot down while it was in their territorial airspace,” Goward explained.
https://www.nationaldefensemagazine.org/articles/2021/2/11/calls-grow-to-find-back-up-systems-for-gps
(Feb. 2021) Can aviation continue to rely on satellite navigation? - EUROCONTROL:
Blog Editor's (Dana A. Goward) Note: With a passenger aircraft almost crashing into a mountain, drones big enough to kill someone crashing in back yards, and
aircraft enroute nearly departing controlled flight, it is no wonder ICAO told its members addressing
GNSS disruption is an urgent priority.
PNT Community members should find this event interesting:
This online event is part of our round of Stakeholder Forum discussions, where we tackle some of the hottest topics in European aviation with a wide range of key
players, within and outside our industry.
Can aviation continue to rely on satellite navigation?
While the answer remains a clear “yes” in most parts of the world, it has also become a clear
“no” in some areas where operations have been affected, especially on
routes between Europe and the Middle East and Asia.
This webinar will explore:
the operational impact of radio frequency interference and how we can continue to ensure safe and efficient operations;
what measures should be taken to limit the proliferation of widespread interference to satellite navigation;
how we can ensure interference-free operations for all users of satellite navigation, including civil aviation, military and other users;
how the combination of space-based and terrestrial systems should evolve in order to deliver resilient infrastructure support to aviation at acceptable costs while
preserving the benefits of satellite navigation.
During the 90-minute webinar, a multi-disciplinary panel will assess these challenges from the operational, regulatory, civil-military and technical perspectives.
https://www.linkedin.com/pulse/can-aviation-continue-rely-satellite-navigation-dana-a-goward/?trackingId=bs1cyL0iKI9o%2FaUlfc4vsw%3D%3D
https://www.eurocontrol.int/event/eurocontrol-stakeholder-forum-uam#register
(Feb. 2021) Skunk Works Is About to Test a Secret New Aircraft Called 'Speed Racer':
Lockheed’s Speed Racer will begin ground testing imminently. Ground testing typically involves watching and testing for reliability, checking for unusual vibrations, and
carrying notional payloads while the aircraft is static or moving under its own power. The next step is actual flight testing.
https://www.popularmechanics.com/military/aviation/a35524610/skunk-works-testing-speed-racer-secret-new-aircraft/?_lrsc=08dffc71-b353-45a4-acf4-a6e2b8f89dd0
(Feb. 2021) Airpower Was Indispensable to Defeating ISIS:
What happened during the air campaign against ISIS? What did airpower contribute to the group's defeat? And what lessons should the
U.S. Air Force and joint force
take from this campaign? This new report explores.
https://www.rand.org/pubs/research_reports/RRA388-1.html
Research Brief related to the above mentioned report:
https://www.rand.org/pubs/research_briefs/RBA388-1.html
(Feb. 2021) Skyborg UAV aims to join frontline US fighter aircraft - GPS World:
It’s only a few weeks into the new year, yet there’s plenty happening in the
UAV world. This month’s question: What’s a Skyborg? The U.S. Air Force awarded contracts
to Kratos, Boeing and General Atomics to prove their approaches to the UAV program.
https://www.gpsworld.com/skyborg-uav-aims-to-join-frontline-us-fighter-aircraft/
(Mar. 2021) Federal policy aimed at GPS interference, critical infrastructure:
March 7, 2021 - By Dana Goward
In its closing days, the Trump administration issued several new policy documents affecting positioning, navigation and timing (PNT) issues.
Some have questioned the long-term impact of these, given the significant policy differences between the previous and current administrations. Yet policies in relatively non-controversial areas such as
PNT are
generally developed by career personnel who tend to remain in place from administration to
administration. While they must adhere to the philosophical tenets of extant elected
officials, these
policies tend to endure longer than others.
Even if this weren’t the case, considering the wealth of other issues the new administration is grappling with,
these new policies could remain in force for some time,
even if the new regime ultimately decides to change them.
Several themes run through many of the documents. These include:
Space-based PNT is vulnerable and must be protected.
America needs to monitor for GNSS disruption.
More sources of PNT than just GPS are needed.
National Space Policy
The first of these late-term documents to be published was the National Space Policy issued on Dec. 9,
2020. Highlights and possible impacts for the PNT community include:
A goal to “Promote and incentivize private industry” could have implications for
low-Earth orbit (LEO) PNT services.
A goal to “Increase the assurance of national critical functions” could include
GPS/PNT resilience.
A pledge to “Safeguard space components of critical infrastructure” undoubtedly
includes GPS. The section also has ominous statements about U.S. responses to purposeful interference and tasks the
Defense and Homeland Security secretaries with having those responses ready.
Another pledge to “Maintain and Enhance Space-based Positioning, Navigation and Timing (PNT) Systems” is followed by
eight explanatory paragraphs, many of which repeat previous policy.
One new item is a promise to invest in detection and mitigation of harmful interference. A mention is also made of the
need for multiple and diverse PNT sources, and responsible use of PNT, echoing the February 2020 Executive Order on the subject. Both of the latter two mentions were in the context of critical infrastructure and mission essential functions versus the security of the nation and economy as a whole.
Report to Congress: GPS Backup Tech Demo
Congress mandated a GPS backup technology demonstration in 2017, and $10 million was subsequently provided for that
purpose. Various internal government delays resulted in the project not getting underway until March 2019. It concluded about a year later.
On Jan. 14, the Department of Transportation (DOT) posted its 457-page
“Complementary PNT and GPS Backup Technologies Demonstration Report” to Congress on its website.
While some people have been critical, it is important to remember the report documents 11 vendor demonstrations, not engineering tests. Technologies were
demonstrated in different locations and under differing conditions.
There is no silver bullet for meeting the nation’s needs. It must be a system of systems.
Also, the amount of effort and equipment in the demonstrations depended in some cases upon infrastructure available and the amount of money the government and vendors were able to spend. This meant that
at least one technology was “demonstrated” mostly by explaining the
concept, and other vendors were able to only partially demonstrate their
technologies.
All of that said, the report offers valuable information about how America should make its national
PNT much more resilient and reliable. First, it reinforces DOT’s message that
there is no silver bullet for meeting the nation’s needs. It must be a system of systems. Second, the report goes further and says what that system of system should look like: “Those technologies are
LF and UHF terrestrial and L-band satellite broadcasts for
PNT functions with supporting fiber-optic time services to transmitters/control
segments.”
From a policy perspective, this is a huge step forward. It resolves previous ambiguity and positions the nation to establish a resilient
PNT architecture, one that will do more than be a “GPS backup.” It will be an architecture that will better support current applications and better enable emerging ones like autonomy,
5G and “NextG.”
National Research and Development Plan for Positioning, Navigation, and Timing Resilience:
Published one hour and fourteen minutes before the end of the administration on inauguration
day, this plan was mandated as part of the February 2020 Executive Order on responsible use of
PNT.
By taking a comprehensive look at how we can do better, it provides an interesting outline of the challenges associated with America’s current over-reliance on
GPS. While not a policy or directive document,
it does suggest two or three departments and agencies that might be tasked with addressing each
challenge.
It also addresses the need for interference detection and monitoring, and diverse sources of
PNT.
U.S. Space-Based PNT Policy (Space Policy Directive 7)
This directive was published five days before the end of the administration and replaced the previous policy, 2004’s NSPD-39.
While the old policy calls for performance monitoring of GPS signals, the new one also
has investment in interference detection and monitoring as a goal.
Perhaps the most significant change in the new policy was the absence of the words “backup capability” and the lack of a mandate for
DOT to lead its establishment. Yet the policy hammers home multiple times the need for more than GPS as a source of PNT. And it doesn’t abandon the idea of government involvement in making that happen.
In addition to reinforcing Executive Order 13905 on responsible use of PNT, the directive defined a new (for presidential policies) term.
“Alternative PNT Service” was described as “a PNT service that has the capability to operate completely independent of, or in conjunction with, other PNT services.” The directive goes on to say that
“Multiple, varied PNT services used in combination may provide enhanced
security, resilience, assurance, accuracy, availability and
integrity. An alternative PNT service allows a user to transition from the primary source of PNT signals in the event of a disruption or manipulation.”
And while the policy does not say the government will establish or support an alternative
PNT service, it comes pretty close. One of its goals is “Invest in… as appropriate, alternative sources of
PNT for critical infrastructure, key resources, and mission-essential functions.”
It goes on to task the departments of Defense, Homeland Security and Transportation with making that happen.
So “backup” is out, “alternative PNT” is in. We agree words are important and are happy to have the new words. Let’s hope the new administration will match the new words with action (as appropriate).
(Mar. 2021) GPS Jammers Essential Tools for UK Car Theft Enterprise:
Blog Editor's Note By Dana Goward: We previously reported on the Mexican government's finding that 85% of truck thefts were aided by
GPS jamming devices. While we have not
found similar national statistics reported in other parts of the world, this case is a reminder that the technology is widely available and in use.
Why wouldn't thieves use it all the time everywhere? It is likely that this is
in fact happening, but many governments either aren't looking, or aren't
publicizing what they find.
Check out the story below that includes the use of "industrial strength" jammers.
Thanks to RNTF corporate member Chronos for alerting us to this story.
https://www.cambs.police.uk/news-and-appeals/Baltors-and-Lukauskas-sentencing-Jan2021
(Mar. 2021) Will We Be Ready if GPS Goes Down? - Wall Street Journal OpEd:
Blog Editor's Note: Ms. Diana Furchtgott-Roth served as the Deputy Assistant Secretary of
Transportation. She is an adjunct professor of economics
at George Washington University, and an RNTF member.
We applaud her commentary in the Wall Street Journal today. We especially like her sum up at the end of the piece:
"Americans depend on GPS too much for the federal government to wait for it to fail. A reliable backup is needed as soon as possible."
Will We Be Ready if GPS Goes Down?:
The Transportation Department has ideas for a backup, but it needs money from Congress.
By Diana Furchtgott-Roth
March 19, 2021 2:05 pm ET
GPS is vital to Americans, but hacking it has never been easier. Protecting the civilian Global Positioning
System, an invisible utility the federal government pays
for, falls to Transportation Secretary Pete Buttigieg NOW.
He would do well to use the results of the Transportation Department’s January
2021 report on technologies that can back up GPS and keep the country moving in
a pinch.
Three separate laws, most recently the Frank LoBiondo Coast Guard Authorization Act of
2018, assign the Transportation Department the task of providing a
backup to GPS. The LoBiondo Act required the secretary to put in place a backup system by the end of
2020, but no funds were appropriated, so the department couldn’t
proceed.
Although Congress hasn’t followed through with the money, the DOT’s new report
lays out a road map.
https://www.wsj.com/articles/will-we-be-ready-if-gps-goes-down-11616177141?st=sgfvpygzru8wchh&reflink=article_email_share
(Mar. 2021) "Dangerous & Costly to Airlines" - EUROCONTROL on GNSS Interference:
Deliberate interference with GNSS by the world's militaries interferes with safe air traffic management, poses risks to aircraft, and imposes extra costs
for fuel and transit time, according to a recent EUROCONTROL stakeholder forum.
2,000% increase in GNSS RFI incidents in 2018 as measured by voluntary incident reporting, with a sustained high rate since;
38.5% of European en-route traffic operates through regions intermittently but regularly affected by
RFI;
5% of traffic in these regions could, given current levels, need special assistance.
Five presentations discussed various aspects of the problem, including that the region of heaviest regular interference was also smack across the highly
traveled route between Europe and south Asia.
A variety of solution and mitigation efforts were suggested. These included a more deliberate monitoring systems to warn aircraft and investigation of an
alternate wide area navigation system not vulnerable to such easy interference. Both of these echoed earlier recommendations of the International
Air Transport
Association.
Another suggestion was that belligerents limit their GPS/ GNSS jammer power to
10W versus the 100W that seems to be the current standard. The
assertion is
that doing so would be equally effective against adversaries while spilling over much less into commercial air traffic operations.
That's an idea. Though given the barrel bombs and nerve gas we have seen used in the region, we are not sure it is
a suggestion that will resonate with many
on the ground.
You can view the entire workshop and access all the presentations here: https://www.eurocontrol.int/event/eurocontrol-stakeholder-forum-gnss#register
(Mar. 2021) DSI to host 2021 Assured PNT Summit in April - GPS World:
February 12, 2021 - By Allison Kral
The Defense Strategies Institute’s (DSI) Assured Positioning, Navigation & Timing (PNT) Summit will take place April 14-15 at the Mary M. Gates Learning Center
in Alexandria, Virginia.
No alt text provided for this image
According to DSI, the event will bring together members of the military services, Department of Defense (DoD),
federal government, industry and academia in a
“town hall” style forum to discuss how important GPS and space-based PNT systems are to the overall resilience of the
warfighter, as well as critical
infrastructure across the United States and abroad.
The 2021 Assured PNT Summit also will offer senior-level insight into how the U.S. military has been a leader in integrating PNT into its everyday operations
and how such capabilities have become vital to the military’s ability to shape the global arena, deter aggression, and fight and win wars.
Confirmed speakers for this year’s event include William Nelson, SES, director, APNT CFT, Army Futures Command; Brig. Gen. Heather L. Pringle,
USAF, commander,
Air Force Research Laboratory; Anthony C. Smith, SES, director, C3I, DoD CIO; Richard De Fatta, SES, director, U.S. Army Space & Missile Defense Center of
Excellence;
Cordell “Del” DeLaPena, SES, program executive officer for Space Production Space & Missile Systems Center,
USAF; Harold W. Martin III, SES, director, National
Coordination Office for Space-Based Positioning, Navigation and Timing; and
Col. Jason Joose, USA, chief of staff/APNT signature effort lead, Army Futures Command.
A number of topics will be covered at the 2021 Assured PNT Summit, including:
Leading current DoD initiatives toward integrating new PNT capabilities to help the Warfighter remain resilient in a dynamic threat environment;
Synchronizing PNT, navigation warfare and space capability development efforts across the
Army to help reduce key capability gaps;
Delivering resilient, affordable and sustainable space capabilities such as modernized GPS to enhance warfighter superiority;
Providing alternate PNT for potential GPS-denied environments; Accelerating the
implementation of cutting-edge Air Force research projects such as NTS-3
GPS Satellite
to provide the most value to the warfighter; Developing critical PNT-related products to enable a Soldier’s PNT capabilities in all warfighting domains;
Overseeing the collection of GPS-related information from multiple federal agencies in an effort
to improve and maintain space-based PNT capabilities;
Advancing efforts to provide GPS protection for all naval air platforms; and
Detailing the Department of Homeland Security plan to test the vulnerabilities of critical infrastructure systems, networks and assets if PNT services were to be
disrupted or manipulated.
https://dsigroup.org/assured-pnt-summit-registration/
(Mar. 2021) What Trump Administration Got Wrong About Protecting GPS Users and America:
MARCH 22, 2021 01:00 PM ET
The Global Positioning System has become the world’s most widely used tech utility.
In February of last year, President Donald Trump reversed long-standing administration policy when he issued Executive Order (13905, “Strengthening National Resilience Through Responsible
Use of Positioning, Navigation, and Timing (PNT) Services.”
The Global Positioning System has become the world’s most widely used tech utility. America’s over-dependence on it for everything from synchronizing cellphone
networks to managing power grids has caused government officials to call it “…
a single point of failure” for the country.
While Trump’s order rightly warned of the dangers in over-relying on GPS, it also shifted away from years of executive branch policy. Rather than focusing on
reinforcing GPS and protecting users with an alternative PNT source or sources, the order told users to protect themselves by accessing commercial services it hoped
would be developed to meet their needs.
GPS signals underlie virtually every technology but are weak, easily blocked and imitated. And many studies have found a reasonable chance the system will be damaged
or destroyed by solar activity within the next 50 years. These vulnerabilities pose a near-existential threat to the nation’s economy and security.
The Trump order’s warning to users—and many of its other provisions—were necessary but they were far from
sufficient.
This is because the order ignored fundamental economic and security realities.
A Free Utility:
America established GPS as its gift to the world in the hope that it would be widely adopted and used. Making the signal free and its specs public were wildly successful.
So much so that as early as 1999 a special commission told President Bill Clinton
that America was likely becoming too dependent on the system.
GPS rapidly became a utility, much like a municipal water system, that serves all citizens in a multitude of ways.
Recognizing GPS’ limitations, a number of companies over the last decade have
tried to develop business models providing backups and alternatives for GPS. While some
have found niche markets with specialized users, just as Evian, Perrier and others have created niche markets for specialized water,
NO alternate PNT provider has been able to
establish a broadly adopted, wide area service. They just can’t compete with the free government service that is
GPS.
The order’s hope of the market providing alternatives—and that millions will be willing to pay a fee to subscribe—is a futile one. Just as few Americans see the need to
purchase a regular alternate supply of household water, few see the need to buy
PNT services to supplement and backup GPS. Besides, if something goes wrong with the water or
with GPS, it’s the utility provider’s fault, not theirs. The government will make sure the problem gets
fixed (hopefully).
A National Security Imperative
The impacts of a prolonged GPS outage or the system’s loss will make
the COVID-19 pandemic look like a warmup act.
Our national government must prevent this as part of its core duty to provide for the common defense and promote the general welfare.
The Trump-era policy promulgated by the order focuses only on critical infrastructure and
large companies that do business with the government.
And it outlines a difficult and unlikely path to protect them.
It largely ignores first responders, local, state and federal
agencies, the Post Office, drone operators, medium and small businesses – in short, about
95%
of current GPS users who help to make the nation function. Not protecting such a large portion of America from an outage
will cripple law enforcement and other first responders,
and greatly diminish our ability to support any sustained military
operations.
And since adversary nations like Russia, China and Iran have terrestrial backup systems,
America will not only be crippled, but we will be weakened far more than those who wish us ill.
In fact, some observers have opined America’s lack of a terrestrial backup system for GPS has already
damaged our national security by providing both terrorists and enemies an
exceptionally attractive target. It has certainly put America at tactical and strategic disadvantages in many situations already.
The Goal: Making the Nation Safer:
Having alternative systems will make GPS satellites and signals less attractive targets and therefore
safer from malicious interference. They will also make the nation safer by
removing a single point of failure vulnerable to solar activity, malicious
threats, and accidents.
But to do that, as many GPS users as possible must also adopt and use one or more alternate
systems.
Anything that inhibits adoption, like limiting it to critical infrastructure, availability only in urban areas, access fees, and the like, reduces protection of the nation.
Even if the complicated Trump plan to coerce large companies into creating systems to protect themselves worked,
it would still provide far less than America needs.
America needs what our adversaries already have: terrestrial PNT systems that are
easily accessed and available to all. Systems that will work in concert with GPS
when it is available and serve in its place when it is not.
https://www.nextgov.com/ideas/2021/03/do-you-see-yourself-room/172734/
(Mar. 2021) Q: How can a GNSS satellite oscillator anomalies, even at micro-scale, be detected?:
https://insidegnss.com/q-how-can-a-gnss-satellite-oscillator-anomalies-even-at-micro-scale-be-detected/
(Mar. 2021) Keeping track of spacecraft as Earth’s water alters its spin:
Mass is constantly being redistributed around our planet, as Earth’s atmosphere, oceans and other bodies of water on and
under the surface melt, shift and stir. This
mass redistribution alters Earth’s center of gravity, which in turn
speeds up and slows down the planet's spin – and so the length of the day – as well as changing
the orientation of its 'spin axis'. These changes to Earth’s spin and orientation occur over
relatively short timescales of days and weeks, and threaten communication
between ground stations and missions in orbit and across the Solar System.
(Mar. 2021) FAA and "Last Gen" Navigation Mentality? - Note to the Reason Foundation:
We always find something of interest in Bob Poole's "Aviation Policy News" from the Reason
Foundation.
This month it is a note he received from a colleague about the FAA and navigation. Bob published in his
"Quotable Quotes" section.
By way of background, the 2001 Volpe report mentioned was the result of a three year, presidentially mandated effort to examine if the
FAA's plan to move
aviation to navigate using only space-based assets (GPS) and do away with terrestrial beacons
(VOR/DMEs) was still a good idea. Clearly being able to do
away with a large network of terrestrial systems would have saved the FAA a lot of money. But the answer was a resounding
"no".
The report also observed that all kinds of transportation, other infrastructure, and
systems in the US were becoming far too dependent upon vulnerable GPS
signals. It recommended the nation investigate establishing an alternate system for when
GPS, for whatever reason, was not available.
The report was published the 29th of August, 2001, less than two weeks before 9/11. Understandably, it took the White House a while to get around to acting
on it. But in December 2004 President Bush issued NSPD-39 which mandated the
Department of Transportation lead a federal effort and establish
a backup capability for GPS.
Folks are still trying to make that happen. Doing so will make GPS a less tempting target for our enemies, and provide another way of getting vital
positioning, navigation, and timing (PNT) services against the inevitability of a prolonged
GPS disruption.
AVIATION POLICY NEWSLETTER:
By Robert Poole
March 22, 2021
Quotable Quotes:
Despite the upcoming 20th anniversary of the Volpe GPS Vulnerability
Study, FAA continues to maintain a GNSS-centric PNT mentality. While their 2016
Performance-Based Navigation (PBN) Strategy was to retain resilient ground-based alternatives, the vast majority of
Distance Measuring Equipment (DME),
VHF Omni-directional Ranges (VORs), and Tactical
Navigation (TACAN) operating in the NAS (National Airspace
System) were designed in the ‘70s and installed
in the ‘80s. Although the concept of “GPS-sole means” does not officially exist,
FAA has NOT yet taken significant steps to recapitalize these
30-40-year-old systems, although efforts to expand procedures reliant on GNSS services continue unabated. By comparison,
FAA installed navaids at over 850
sites in the 1980s and added over 100 additional locations in the 1990s. It is interesting that their current
DME-VOR-TACAN (DVT) plan spans 42 years—over
twice the normal life cycle of these equipments—and does NOT address the hundreds of aging
Instrument Landing Systems (ILS) or Approach Lighting
Systems
(ALS). It is also interesting that FAA’s proposed DVT strategy is to issue
Indefinite Delivery/Indefinite Quantity (ID/IQ) contracts, with
TACAN antenna
replacement being the first step. This will only serve to proliferate and expand the logistics challenges of maintaining numerous configurations by an
aging and retiring workforce, preclude economic ordering quantities, and take decades to replace thousands of aging navaids. As reports of
GNSS interference
with aviation continue to mount worldwide, it would seem prudent for FAA to prioritize the replacement of these resilient systems to ensure, as the
FAA
mission states, ‘the safest, most-efficient aviation system in the world,’ and
set an example for ANSPs worldwide.”
—Aviation Sector Professional, email to Robert Poole, March 15, 2021
LINK: https://reason.org/aviation-policy-news/few-u-s-airports-being-leased-climate-change-problem-grows-and-more/
(Mar. 2021) Industry members, non-profit urge Congress to fund GPS alternatives - GPS World:
RNT Foundation decided to sign this letter with members of industry, some of which are our members, some are not, because it does not promote an individual technology
or company. Rather it reinforces the work and findings of the Department of
Transportation.
In separate letters to members of the House of Representatives and the
Senate, seven companies and a non-profit URGED Congress to support alternative
positioning,
navigation and timing systems (PNT) with the “necessary funds and other appropriate policy tools.”
Signing the letter were NextNav, UrsaNav, Satelles, Hellen Systems, OPNT, Orolia, Microchip, and the non-profit Resilient Navigation and Timing Foundation
(RNTF).
The letters focus on and endorse the system-of-systems approach outlined in the Department
of Transportation’s (DOT) recent report to Congress on the results of
its GPS Backup Technology Demonstration. The report found an adequate and robust American PNT system should include space-based L-band signals,
low-frequency (LF)
and ultra-high-frequency (UHS) signals, and fiber connections between the
terrestrial LF and UHF transmitters.
“Our country depends on GPS for critical infrastructure, and there is an urgent need for resiliency being built into our critical infrastructure. Before the report
came out, some of us had different ideas of how the U.S. should go forward,” said
Ganesh Pattabiraman, CEO of NextNav. “But the DOT report provided the data to make
it very clear that it is a combination of technologies that need to come together to truly enable nationwide backup to
GPS, and it was good to see we could get
industry alignment on the findings.”
The letters describe many of the threats to GPS, both natural and malicious; its vulnerabilities; and the dire consequences of disruptions. They go on to state that
robust, more reliable PNT is needed for emerging and future systems like
E911, 5G, resilient electrical grids, drones and other automated systems.
Monty Johnson, CEO of OPNT, a provider of time-over-fiber services, praised the findings of the
DOT report. “The key to resilience and reliability in a system-of-systems
is including technologies that deliver the same information using starkly different means. It is hard to imagine a combination of technologies that are more diverse than
fiber, satellites, LF and UHF.”
According to Pattabiraman, the signers of the letter agree that the DOT report made clear that there are mature technologies available today that can address the
GPS
backup issue. DOT and Congress now have the data to act to enable a much-needed resilient infrastructure for the country.
Dana A. Goward, president of the non-profit RNT Foundation, agreed. He also observed that deciding on the technologies and congressional funding were important, but only
first steps. “The goal of this effort is not to just implement systems,” he said.
“it’s to make America safer. Establishing the services quickly and efficiently will be key,
as will ensuring they are widely adopted.”
“Protecting the nation from the consequences of a space-based PNT disruption will require that these systems be accessed and used by a wide variety of users from first
responders and delivery services, to all forms of critical infrastructure,” Goward said. “This means the government will need to eliminate as many barriers to adoption as
possible. One or more of these alternatives has to be available to every American. And a basic level of service has to be free, just like the
GPS utility it is reinforcing.
Fortunately, we estimate this can be done relatively inexpensively. It will be only a small fraction of the
$1.7B we spent on GPS last year.”
that there are mature technologies available today that can address the GPS backup
issue. DOT and Congress now have the data to act to enable a
much-needed resilient infrastructure for the country.
The alternative to making this relatively modest investment, according to Goward, is unacceptable.
“There are lots of threats to GPS,” he said. “Take the sun for example. The most recent study I saw estimates a
70% chance solar activity will damage the GPS constellation
in the next 30 years and a 20% chance it will destroy a big part of it. And the sun is just one of the threats we face. We can’t keep playing this kind of Russian Roulette
with the fate of our nation. Especially when other countries like Russia and China have already taken steps to protect themselves with terrestrial
systems.”
A copy of the letter sent to Senators can be found here, and the one to members of the House of Representatives here:
https://rntfnd.org/wp-content/uploads/House_GPS-Backup-MultiSig-Mar-2021.pdf
(Mar. 2021) NIST Team Compares 3 Top Atomic Clocks With Record Accuracy Over Both Fiber and Air:
In a significant advance toward the future redefinition of the international unit of time, the second, a research team led by the
National Institute of
Standards and Technology (NIST) has compared three of the world’s leading atomic clocks with record accuracy over both air and optical fiber links.
Described in the March 25 issue of Nature , the NIST-led work is the first to compare three clocks based on different atoms, and the first to link the most
advanced atomic clocks in different locations over the air. These atomic clock comparisons place the scientific community one step closer to meeting the
guidelines for redefinition of the second.
Thomas H. Kerr III comment: "These important comparisons make technologists better able to confirm the utility of these various time sources to support the
system-of-systems approach to resilient PNT (beyond mere reliance on just GPS/GNSS) by augmenting its accuracy."
(Mar. 2021) GPS Allies Say Timing Supplement Within Reach - Communications Daily:
https://communicationsdaily.com/biography/matt-daneman-465543
(Apr. 2021) Terrestrial navigation system ready for use in S. Korea to cope with jamming and electric warfare - Aju Business Daily:
Notice the "advantage" South Korea has of a belligerent, not-at-all-subtle enemy. Our adversaries only jam GPS in areas outside the United States (as far as
we know) so we are not nearly as concerned. Hence we are far more vulnerable and at risk than South Korea. We are at risk from Russia, China, sophisticated
terrorists, human error, solar activity...the list goes on.
If only we had better enemies!
Lim Chang-won Reporter(cwlim34@ajunews.com) | Posted : April 1, 2021, 10:17 | Updated : April 1, 2021, 10:17:
SEOUL -- To cope with unexpected interference such as North Korea's electric warfare, South Korea will launch an uninterrupted positioning navigation service
based on radio waves from ground transmitters instead of satellites, starting with a pilot project in June for coastguard vessels and state patrol boats
operating in volatile border areas off their west coast.
South Korea began developing a terrestrial navigation system that can provide Positioning
navigation timing (PNT) information reliably by utilizing transmission
towers on the ground in 2016 after North Korea discharged strong electric waves for systematic cross-border
electronic warfare. The electric wave attack caused
no visible damage, but Seoul condemned it as a serious provocation.
PNT information, which is essential for industry and daily life, relies on the U.S.
Global Positioning System (GPS). With multiple disruption tools, North
Korea has occasionally jammed GPS communications in South Korea. Seoul regards
GPS disruptions as a new form of North Korea's low-level, asymmetric
provocation.
In a statement published on 31 March 2021, the Seoul government announced the commercialization of an enhanced long-range navigation
(eLoran) system that
provides precise visual information and calculates location by measuring the time reached by radio waves from three or more transmitters.
A pilot service will be launched on 1 June 2021, with South Korean Coast Guard vessels and patrol boats operating in maritime border areas to receive
eLoran
receivers. The service will be expanded to fishing boats and merchant ships. For a nationwide service, South Korea will establish a cooperative system with
broadcasting, information and communication sectors to provide precise standard-time information and expand it to other industries to prevent disruptions in
national infrastructure even when GPS is suspended.
READ MORE: https://www.ajudaily.com/view/20210401091701262
(Apr. 2021) Next Steps in GNSS Receiver Security Validated with OSNMA Testing - Inside GNSS - Global Navigation Satellite Systems Engineering, Policy, and Design:
https://insidegnss.com/next-steps-in-gnss-receiver-security-validated-with-osnma-testing/
(Apr. 2021) “The Mounted PNT [Positioning, Navigation and Timing] program and the APNT CFT
are continuously evaluating all the PNT technologies available to enable assured
PNT to Army forces anywhere in the world.” said Lt. Col. Alexander “Raz” Rasmussen.
“A part of this effort is the recently established PNT Modernization
project office. PNT Modernization’s mission is to evaluate and test
PNT technologies available
across industry, academia, and government labs. Based on applicability,
mission need, and maturity, PNT technologies will be accelerated for integration into
MAPS
[Mounted Assured PNT System]. We must continue to provide
‘fight tonight’ capability to Soldiers worldwide while accelerating technologies that maintain threat overmatch in the future.”
More MAPS info here: https://lnkd.in/d2jXP7e
https://peoiews.army.mil/maps-unprecedented-speed-for-unprecedented-times/
(Apr. 2021) Lockheed scores $1.1B contract to build US Army’s guided rocket on heels of extended-range test:
https://www.defensenews.com/land/2021/03/30/lockheed-scores-12b-contract-to-build-us-armys-guided-rocket-on-heels-of-extended-range-test/
(Apr. 2021)
Blog Editor's Note: Great article by our friend Logan Scott. While the DOT report on their GPS Backup Tech Demo does have a lot of
information, we have to
agree it is not the be all and end all on the question of "GPS backups" as some would like.
Logan observes:
"While I don’t disagree with the general assessments, there is considerable hazard in applying them blindly to select a national
strategy."
One challenge he notes is that not all candidate technologies were demonstrated. He cites
PNT via 4G and 5G as one example. Also, systems like Australia's
Locata and WWV were not included.
We agree, by the way, that 5G, especially has potential, though it still needs a solid timing backbone to be resilient and independent of
GNSS.
As for WWVB, it certainly has potential and is in operation. Yet, WWVB operates at
60KHz, not that far from eLoran at 100KHz. All the engineering and
many of the PNT standards have been done for eLoran and it is in use elsewhere in the
world. Not so for WWVB. He makes a number of other cogent points
especially about resilience. We encourage you to follow the link below and read his article.
We have to agree with Logan that the biggest draw back to the DOT report is that
folks are going to read too much into what was, not engineering trials and
evals, but a set of vendor demos. As such they were limited by being performed in different locations and under different conditions.
Some of which were
the result of a lack of funds to perform a full demo of the technology.
The biggest plus to the project and report was it's finding the correct path forward for the nation is a system-of-systems approach with technologies that
have starkly different failure modes.
Now we just need the government to stop admiring the problem and follow through on its decades-old promise to
act.
State of Play: Resilience Is Not Just About Parts!
March 19, 2021
By Logan Scott
LINK TO ARTICLE DISCUSSED ABOVE: https://insidegnss.com/state-of-play-resilience-is-not-just-about-parts/
(Apr. 2021) The Rising Threat to the Integrity of Maritime Navigation Data - The Maritime Executive:
Blog Editor's Note: A good update article by George Shaw of the General Lighthouse Authority of UK and
Ireland. This is the kind of issue that tends to fall
into the background for users. Regular updates like this help keep it in the forefront of people's minds making mishaps less likely.
We note that the US Coast Guard has identified this as a significant maritime cyber
concern, and the International Maritime Organization has dubbed it a urgent
safety of navigation issue.
Of course, if mariners had another wireless source of PNT that was difficult to disrupt to work with and reinforce
GNSS, this would be MUCH less of a problem
and danger.
The Rising Threat to the Integrity of Maritime Navigation Data:
By George Shaw
Loss of satellite signal is a well-known operational risk, but few mariners are aware of the threat of GNSS providing a false
time, position or direction even
when still available. When these position errors exceed a safe margin of error, they can cause ships to derive and transmit dangerously misleading
Information.
GNSS is not designed with inherent real-time integrity, which refers to the
users’ ability to trust the data and receive timely warnings if it is unreliable.
READ MORE: https://www.maritime-executive.com/editorials/the-rising-threat-to-the-integrity-of-maritime-navigation-data
(Apr. 2021) The $1.5 billion Space Fence can track tiny objects in low Earth orbit as small as a marble:
https://spacenews.com/space-fence-surveillance-radar-site-declared-operational/
(Apr. 2021) It’s Time To Declare Space Systems As Critical Infrastructure - Politico:
Blog Editor's Note: This article proposes an idea that has been raised periodically, either designating
GPS as critical infrastructure or, as in this case, space systems generally.
The overall goal is to provide greater visibility and focus on the importance and criticality of space systems. Presumably this would lead to greater efforts to ensure they are
properly protected and secure.
Believe it or not, a big challenge to designating GPS as critical infrastructure has been that
GPS is a government system.
The Department of Homeland Security (DHS) is responsible for critical infrastructure protection. It has designated 16 critical infrastructure sectors to protect. Some
examples are the transportation sector, chemical sector, and the energy sector. The way
DHS tries to protect infrastructure is by gathering commercial entities from
each sector in various forums to discuss issues, develop best practices, gain understanding, consider possible government actions, etc.
Not a model that could be applied to a government owned satellite system like
GPS.
It might be one that could be applied to commercial space. If so, the next question would be whether the appropriate government lead would be
DHS, NASA because
they have the technical expertise, Commerce as suggested by the authors, or some other entity. Perhaps It could be a non-governmental entity. Maybe a beefed up version
of the Space Information Sharing and Analysis Center.
It’s time to declare space systems as critical infrastructure
Such a move "would galvanize the policy and stakeholder attention and resources needed to secure these systems," argue two government space experts.
By EDWARD SWALLOW and SAMUEL VISNER
04/02/2021 06:45 AM EDT
Edward Swallow is the senior vice president for civil systems at The Aerospace
Corporation, a nonprofit which operates a federally funded research and
development center for the U.S. space enterprise. Samuel Visner is a technical fellow and
former director of the National Cybersecurity FFRDC at MITRE.
They are also founding members of the Space Information Sharing and Analysis Center Board of Directors.
In the United States, our economy, national security and everyday lifestyle rely heavily upon thousands of space systems in orbit.
For instance, the Global Positioning System is vital for shipping and
transportation, including ground, air traffic and marine navigation — anywhere in the
world. Communication and information processing, including the world’s developing
5G networks, rely heavily on space-based infrastructure. Space-based
systems are also critical for national security missions that protect our homeland and enable operations overseas. We have long counted on satellites for
command and control
of our armed forces, missile guidance, early warning and
intelligence.
READ MORE: https://www.politico.com/news/2021/04/02/its-time-to-declare-space-systems-as-critical-infrastructure-478848
(Apr. 2021) Secure World Foundation Says Russia is Testing New LEO, GEO Anti-Satellite Technologies - Via Satellite:
https://www.satellitetoday.com/government-military/2021/04/06/secure-world-foundation-says-russia-is-testing-new-leo-geo-anti-satellite-technologies/
The Secure World Foundation released a report suggesting that Russia is testing new
Anti-Satellite (ASAT) and Direct Ascent Anti-Satellite
(DA-ASAT) technologies
that could threaten spacecraft in Low-Earth Orbit (LEO), and eventually,
Geostationary Orbit (GEO).
In the April 2021 report, “Global Counterspace Capabilities: An Open Source Assessment,” co-authors
Brian Weeden and Victoria Samson wrote that Russia is
recapitalizing ASAT capabilities they had during the Cold War and testing Rendezvous and Proximity Operations (RPO) technologies in both
LEO and GEO.
“…Some of those efforts have links to a Cold War-era LEO co-orbital
ASAT program,”
Weeden and Samson wrote. “Additional evidence suggests Russia may have started a new co-orbital
ASAT program called Burevestnik, potentially supported by a
surveillance and tracking program called Nivelir. … While Russia is actively testing what appears to be a new
DA-ASAT capability in their Nudol system, it is
not yet operational and does not appear to have the capability to threaten targets beyond
LEO.”
The report acknowledges the possibility that these technologies could also be used for non-aggressive surveillance of foreign satellites and notes that most
of Russia’s on-orbit RPO activities seem to fit that scenario so far. “However,
Russia has deployed two ‘sub-satellites’ at high-velocity, which suggests at
least some of their LEO RPO activities are of a weapons nature,” the report
said.
In April of last year, CNBC and other news outlets reported that U.S. Space Force generals believed that Russia successfully tested a missile capable of
destroying a LEO satellite. Military officials called the test “unusual and disturbing.”
The Secure World Foundation report also studied development of militarized space capabilities in China and the United
States. The report noted that China has
conducted multiple tests of RPO technologies in both LEO and GEO, which could lead to co-orbital
ASAT capabilities. “However, as of yet, the public evidence
indicates [China] has not conducted an actual destructive co-orbital intercept of a target, and there is no public proof that these
RPO technologies are
definitively being developed for counterspace use as opposed to intelligence gathering or other purposes,” said Weeden and Samson.
In regard to the United States’ anti-satellite technologies, Secure World Foundation said that
the U.S. military, like China, has conducted multiple RPO
tests in both LEO and GEO that could lead to a co-orbital ASAT
capability, but that there is no evidence of an operational system.
Interestingly, the report notes that the United States has conducted significant research and development on the use of ground-based high energy lasers for
potential counterspace purposes. “We assess that there are no technological roadblocks to the U.S. operationalizing [lasers] for counterspace applications.
With its SLR [Satellite Laser Ranging] sites and defense research facilities, the United States possesses low power laser systems with the capability to
dazzle, and possibly blind, EO imaging satellites.”
(Apr. 2021) An hour of your time. The United States must implement the foundations for artificial intelligence across the whole of government before
2025. We've not a moment to lose.
https://lnkd.in/dXKnnbB
DoD Joint Artificial Intelligence Center:
21,435 followers
The Vice Chairman of the National Security Commision on #AI Robert Work and
JAIC Director LtGen Michael Groen addressed the media yesterday to discuss #artificialintelligence in the
United States Department of Defense. Watch it here: #nationalsecurity
Powerful statements by Vice Chairman Work and JAIC Director Groen.
We stand ready to support the 'Digital Corps'. Our recent delivery of the AI-powered application to the Undersecretary of Defense serves as a proof of both our capability and commitment in this area.
Summit2Sea Consulting Erica Thomas Megan Foster, MBA Bryan Eckle Laurian (Schwallie) Eckle Eric Dorsey
-------------------------------------------------------------------------------------------------------
Independent Linkedin Reader's comment: "Well done DoD Joint Artificial Intelligence Center"
------------------------------------------------------------------------------------------------------
Independent Linkedin Reader's comment: "3-star General Michael Groen reminds me of 4-star General James N. Mattis had the latter been cyber-focused."
-----------------------------------------------------------------------------------------------------------
Independent Linkedin Reader's comment: Couldn’t agree more. The larger challenge was well stated by Thomas Friedman in the New York
Times next.
China Doesn’t Respect Us Anymore — for Good Reason:
Sometimes a comedian cuts through foreign policy issues better than any diplomat. Bill Maher did that the other week with an epic rant on U.S.-China relations, nailing the most troubling contrast between the two countries: China can still get big things done. America, not so much.
For many of our political leaders, governing has become sports, entertainment or just mindless tribal warfare. No wonder China’s leaders see us as a nation in imperial decline, living off the leftover fumes of American “exceptionalism.” I wish I could say they were all wrong.
“New Rule: You’re not going to win the battle for the 21st century if you are a ‘silly people.’ And Americans are a silly people,” said Maher. “That’s the classic phrase from ‘Lawrence of Arabia’ — when Lawrence tells his Bedouin allies that as long as they stay a bunch of squabbling tribes, they will remain ‘a silly people.’ …
“We all know China does bad stuff. They break promises about Hong Kong autonomy; they put Uyghurs in camps and punish dissent. And we don’t want to be that. But it’s got to be something between authoritarian government that tells everyone what to do and a representative government that can’t do anything at all.”
Maher added: “On a national level, we’ve been having Infrastructure Week every week since 2009, but we never do anything. Half the country is having a never-ending ‘woke’ competition. … The other half believes we have to stop the lizard people, because they’re eating babies. … China sees a problem and they fix it. They build a dam. We debate what to rename it.”
Yes, China has huge problems. Its leaders are not 10 feet tall, but they are focused on real metrics of success. “China’s leaders are fierce but fragile,” argues James McGregor, the chairman of the consultancy APCO Worldwide, Greater China. “Precisely because they were not elected, they wake up every day scared of their own people, and that makes them very focused on performance” — particularly around jobs, housing and clean air.
By contrast, many U.S. politicians these days are elected from safe, gerrymandered districts and seek to stay in power by just “performing” for their base with populist theatrics.
Whenever I point this out, critics on the far right or far left ridiculously respond, “Oh, so you love China.” Actually, I am not interested in China. I care about America. My goal is to frighten us out of our complacency by getting more Americans to understand
that China can be really evil AND really focused on educating its people and building its infrastructure and adopting best practices in business and science and promoting government bureaucrats on merit — all at the same time. Condemning China for the former will have zero impact if we’re not its equal in all of the latter.
At last week’s Alaska meeting between America’s and China’s top diplomats, Chinese officials made it quite clear that they no longer fear our criticism, because they don’t respect us as they once did, and they don’t think the rest of the world does, either. Or as Yang Jiechi, China’s top foreign affairs policymaker, baldly told his U.S. counterparts: “The United States does not have the qualification …
to speak to China from a position of strength.”
Europe Plunders Paris for Talent, and P.S.G. Pays the Price
Surprised? What did you think, that the Chinese didn’t notice that our last president inspired his followers to ransack our Capitol, that a majority of his party did not recognize the results of our democratic election, that a member of our Congress believes that Jewish-run space lasers cause forest fires, that left-wing anarchists were allowed to take over a section of downtown Portland, creating havoc for months, that during the pandemic the U.S. printed money to help its consumers keep spending — much of it on Chinese-made goods — while China printed money to invest in even more infrastructure, and that gun violence in America is out control?
My message to China is: Be careful. Some of your diplomats sound awfully arrogant. As the proverb says: “Pride goeth before destruction, and a haughty spirit before a fall.” America still excels in a lot of areas.
But my message to my fellow Americans is: We now have to return to and double down on what was our formula for success.
And that is: educating our work force up to and beyond whatever technology demands; building the world’s best infrastructure of ports, roads and telecommunications; attracting the world’s most energetic and high-I.Q. immigrants to enrich our universities and start new businesses; legislating the best regulations to incentivize risk-taking while curbing recklessness; and steadily increasing government-funded research to push out the boundaries of science so our entrepreneurs can turn the most promising new ideas into start-ups.
On this front there is some hope, noted McGregor: “Congress has begun sorting through the hundreds of China bills introduced in the last Congress to forge bipartisan legislation to invest in science and technology, R&D and U.S. leadership in the same technologies that China has declared as the next frontiers.” And President Biden is talking about spending trillions!
Nothing could be more important. Because good ideas — respect for human rights, democracy, an independent judiciary, free markets, protection for minorities — don’t just win in the world because they are good ideas. They diffuse and are embraced because others see them producing justice, power, wealth, opportunity and stability in countries that practice them.
American ideals infused every global institution in the 20th century because we were powerful, and we were powerful because more often than not we implemented our ideals.
But, if we as a country continue to act as we have of late — “dumb as we want to be” — then our power will be diminished and with it the power of our ideals. We will have steadily less influence on China and on the world at large no matter how loudly we chant “U.S.A., U.S.A., U.S.A.” So, let’s make sure we win the Olympics that count.
The Times is committed to publishing a diversity of letters to the editor. We’d like to hear what you think about this or any of our articles. Here are some tips. And here’s our email: letters@nytimes.com.
Follow The New York Times Opinion section on Facebook, Twitter (@NYTopinion) and Instagram.
Thomas L. Friedman is the foreign affairs Op-Ed columnist. He joined the paper in 1981, and
has won three Pulitzer Prizes. He is the author of seven books, including
“From Beirut to Jerusalem,” which won the National Book Award.
(Apr. 2021) Secure World Foundation Says Russia is Testing New LEO, GEO Anti-Satellite Technologies - Via Satellite:
https://www.linkedin.com/pulse/secure-world-foundation-says-russia-testing-new-leo-geo-goward/?trackingId=Vu8No%2FuPGW%2B1ZrfahbomTQ%3D%3D
Blog Editor's Note: This article talks about Russia's activities at LEO and
GEO.
Of course, even though GNSS are at MEO, this should still be a concern for the PNT community for several reasons.
Some nations have some PNT at GEO and/or LEO, and others are considering it, either with dedicated constellations, or as a part of other systems, such as
OneWeb. China reportedly has PNT capability in all three orbit regimes, for example.
Also, you have to pass through MEO to get from LEO to GEO. Clearly, Russia could easily cause mischief in
MEO, if they wanted to. They probably are avoiding MEO so as to not interfere with
GNSS, including their own GLONASS, and because the US has said that any interference with GPS in space will be considered an attack on the nation
itself.
And, as we have noted before, countering GNSS with electronic warfare with assets like Russia's reported space-based nuclear powered jammer, will be easier and more effective than attacking one or two of the satellites. So they already have what they need. And no need to test it.
Secure World Foundation Says Russia is Testing New LEO, GEO Anti-Satellite Technologies
By Jeffrey Hill | April 6, 2021
The Secure World Foundation released a report suggesting that Russia is testing new
Anti-Satellite (ASAT) and Direct Ascent Anti-Satellite
(DA-ASAT) technologies that could threaten spacecraft in Low-Earth
Orbit (LEO), and eventually, Geostationary Orbit (GEO).
In the April 2021 report, “Global Counterspace Capabilities: An Open Source Assessment,” co-authors
Brian Weeden and Victoria Samson wrote that Russia is recapitalizing
ASAT capabilities they had during the Cold War and testing Rendezvous and
Proximity Operations (RPO) technologies in both LEO and
GEO.
“…Some of those efforts have links to a Cold War-era LEO co-orbital ASAT
program,” Weeden and Samson wrote. “Additional evidence suggests Russia may have started a new
co-orbital ASAT program called Burevestnik, potentially supported by a surveillance and tracking program called
Nivelir. … While Russia is actively testing what appears to be a new DA-ASAT capability in their
Nudol system, it is not yet operational and does not appear to have the capability to threaten targets beyond
LEO.”
READ MORE: https://www.satellitetoday.com/government-military/2021/04/06/secure-world-foundation-says-russia-is-testing-new-leo-geo-anti-satellite-technologies/
-------------------------------------------------------------------------------------------------
Independent Comment #1 from Linkedin Reader: A powered jammer from space will have next to no impact, on a
LF (30 to 300 kHz) and MF (300 to 3000 kHz) ground based PNT
technology. As atmospheric attenuation is becomes very high below 5 MHz in
frequency, making powered jammers more of a local issue. With these low band terrestrial systems, this highlights the need for both a
GNSS and terrestrial systems to operate side by side.
Independent Comment #2 from Linkedin Reader: which is why land based microPNT is so important.
Independent Comment #3 from Linkedin Reader: They actually don't have to develop very much from scratch,
as everything is already handed over via various "helpers".
https://www.wearethemighty.com/mighty-history/star-wars-program-33-years-later/
"In 1996, the Pentagon pushed for the development of an airborne laser weapon system. The result was a modified Boeing 747 with tracking lasers and a
chemical oxygen iodine laser (COIL). The Airborne Laser’s first
flight was over Kansas in July 18, 2002 and, after a series of flight tests, the
COIL laser was test-fired in September 2008.
According to the Arms Control Association, the major issue with the airborne laser was that it wasn’t powerful
enough, had limited range, and made the 747 vulnerable to anti-aircraft missiles.
The airborne laser’s shortcomings led Defense Secretary Robert Gates to cancel the program in 2010."
https://abcnews.go.com/US/history-us-missile-defense-systems/story?id=47753516
Inependent Comment #4 from Linkedin Reader: My only question is why it’s taken so long for all major powers to develop a hard-kill option for Satellites.
Independent Comment #5 from Linkedin Reader: I would say because the "target" gets more valuable the more the vulnerable technology is integrated into critical systems.
This is why people believe the multiple PNT systems will minimize the incentive to disrupt any particular one of them. "Sole source GPS" after decommissioning or obsoleting ground systems is an obvious high value target.
Independent Comment #6 from Linkedin Reader: John H. Johnson Sr. Agreed. Makes sense.
The bigger the satellite constellation for the positioning system, the harder the targeting problem for a “hard-kill” solution in its space-based segment. It’s resilience is the challenge so the exploitable weakness may lie elsewhere in the systems architecture or in its EM
domain.
(May 2021) More on Moore's Law:
https://newsroom.ibm.com/2021-05-06-IBM-Unveils-Worlds-First-2-Nanometer-Chip-Technology,-Opening-a-New-Frontier-for-Semiconductors
(May 2021) ‘Take the bullseye off GPS before it’s too late!’ — PNT leaders at GWU webinar - GPS
World
May 7, 2021 - By Dana Goward
A May 5 webinar about the GPS Backup Technology Demonstration by the U.S.
Department of Transportation (DOT) provided valuable insights about the project and
intended way forward for PNT efforts in the department.
It also evolved into a policy discussion with former government leaders saying establishing alternative
positioning, navigation, and timing (PNT) systems
would make GPS safer by “taking the bullseye off,” and that “the time is now, before it is too late.”
The webinar, entitled “What Technologies Can Secure GPS?”, was hosted by the Space Policy Institute at
George Washington University (GWU). A bipartisan
constellation of civil PNT stars gathered to participate in the event.
Featured in the webinar were:
introductory remarks by Robert Hampshire, chief scientist for the U.S. Department
of Transportation (DOT). He has also been nominated to be DOT’s assistant
secretary for research and technology.
a presentation by Karen Van Dyke, director, Positioning, Navigation and Timing for
DOT, and Andrew Hansen of DOT’s Volpe Transportation
Systems Center.
discussion of the issues by Diana Furchtgott-Roth, adjunct professor at GWU and a DOT deputy assistant secretary during the Trump administration, and Greg
Winfree, director of the Texas Transportation Institute at Texas A&M University and DOT assistant secretary during the Obama administration, both of whom
led civil PNT issues for the federal government during their time in office.
Scott Pace, director of GWU’s Space Policy Institute, serving as moderator; he was executive
secretary of the Space Council during the Trump administration.
Hampshire opened the event with an address that touched on Biden administration themes of “building back better,” modernizing infrastructure, reducing
transportation deaths, making transportation more efficient, and preserving America’s technological leadership.
All of these were linked to the need to
improve PNT resiliency and reliability.
Backup tech demo did not close any doors
Van Dyke and Hansen then gave a presentation on the results of the department’s technology demonstration project.
Van Dyke pointed out that, while “GPS backup” may be a popular term, we need complementary capabilities that come into play
not just when GPS is unavailable
but work alongside it and provide additional capability and resilience all the
time.
She also mentioned that the department is well aware there are more candidate technologies than those selected for the demonstration. Companies offering
other ways of providing PNT will not be excluded from future consideration and efforts just because they were not part of the demonstration project.
Also, while the government collected the data during the demonstrations, she acknowledged that the effort was designed to “showcase the technologies in their
best light.” Further study, stress testing, and evaluation will be needed for any system or technology that might be of interest to the government.
Key elements in the demos
Hansen discussed the particulars of how the technology demonstrations were conducted and some of the results. While the department evaluated
14 measures of
effectiveness during the project, Hansen said that two were key — accuracy and coverage per unit of infrastructure.
All the technologies demonstrating timing showed accuracy that would be useful across a wide range of applications, he said.
Positioning accuracy, though,
varied from a “ones of meters to around 300 meters” depending on the technology.
Hansen said that coverage per unit of infrastructure varied exceptionally between the technologies. These included satellite systems that provide global
coverage with a fixed infrastructure, and radio frequency systems with widely different coverage areas per transmitter.
He also observed that the technology demonstration project was not the end of the department’s technical inquiries. In fact, some of its results—such as
eLoran performance in an underground scenario—were unexpected and are being further examined.
Transportation has some of the most stringent PNT requirements for accuracy, integrity, availability, and reliability, he said. And not all safety-critical
transportation requirements may be met by market-based business models. Commercial systems lack the open standards and specifications that have made
GPS so
useful and widely adopted. Hansen said that the department will be working on these issues going forward, as well as performance monitoring for alternative
systems.
A recurring theme throughout the webinar from all participants was that there is no single solution, no silver bullet, to achieve sufficient national
PNT
resilience. A systems-of-systems approach was needed. In Hansen’s words “a plurality of complementary systems” is required to ensure
PNT reliability and
safety, as well as efficient transportation.
Take the bullseye off GPS! — An urgent national security issue
While agreeing with the systems-of-systems approach, Greg Winfree pointed out that a first step still needs to be taken. He said that the nation has known
about the need for alternate PNT since a 2001 report by DOT’s
Volpe Center. Twenty years later, still no long overdue first step has been taken.
Just establishing the first alternative and complementary system, Winfree said, will make
GPS and the United States much safer. “We need to take the bullseye
off of GPS,” he said. GPS is so critically important to this country that it is a very attractive target for those who would do us harm. Having even one just
alternative in place would make it much less of a target.
Diana Furchtgott-Roth pointed out that China, Russia, Iran and others have terrestrial systems that complement space-based
PNT. About establishing
alternatives, she said “The time is now, before it’s too late.”
Provisions in the United States National Space Policy provide that “[a]ny purposeful interference with or an attack upon the space systems of the United
States or its allies that directly affects national rights will be met with a deliberate response at a time, place, manner, and domain of our choosing.”
Scott Pace also commented that an having an alternative to GPS will contribute to national security and improve global stability.
It will “lower the
pressure on us to escalate and respond” should GPS satellites be damaged, or services
disrupted, he said.
Next steps
One of the questions posed at the end of the session was about actions and expected accomplishments in alternate
PNT at DOT in the next 18 months. When could
the first alternative system be expected?
The DOT technology demonstration report recommended that the department work next to develop standards and requirements for alternative systems. Current
government employees were appropriately reluctant to say much more.
Calling upon her recent experience in government, however, Diana Furchtgott-Roth that said she believed that the department needed time to stress test
technologies, develop standards and finalize requirements. Since many capable technologies were mature, some already in operation, she thought the first
capability could be up and running within a year after that.
The only missing element according to Furchtgott-Roth is funding, and the focus needs to be on motivating Congress to provide it. The stage is set, she said,
with all parties agreeing on the importance of resilient PNT.
She observed that it is very difficult to get the two parties in Congress to agree, and to pass legislation. Yet
this has happened three times in support of
establishing GPS alternatives. And PNT is such a critical capability that the entire executive branch even came together to protect it last year opposing
the FCC’s decision in the Ligado Networks application.
She also related that, when she was in office, she requested $15M for the current fiscal year to do needed stress testing and standards development,
but the
funding did not appear in the budget.
One reason could have been questions she was asked about whether it is the government’s job to pay for an alternative to
GPS, she said.
As a conservative economist, her answer was and is a resounding “Yes.” The national need is beyond the business model of one company or private entity. That
is something also suggested in DOT’s report on the tech demo.
Also, “enormous value and vast efficiencies” come from one entity funding such a utility, she said. “Just as the government funds national defense,
it should
also provide a complement to GPS.”
George Washington University’s Space Policy Institute reports a recording of the webinar will be
posted on YouTube within the next week.
https://www.gpsworld.com/take-the-bullseye-off-gps-before-its-too-late-pnt-leaders-at-gwu-webinar/
(May 2021) Just how resilient are satellites?:
https://www.datacenterdynamics.com/en/analysis/just-how-resilient-are-satellites/?utm_content=bufferf1097&utm_medium=social&utm_source=linkedin.com&utm_campaign=buffer
(May 2021) Emergency Landing - Russia Still Jamming Hard in Ukraine:
Blog Editor's Note: This report from the Organization for Security and Cooperation in Europe is no surprise. We have reported on this before and Russia is
still Russia. They have bragged their jamming capability extends for hundreds of
kilometers, so per the report, hard to say where it is coming from.
Always good to be reminded, though, that threats are still out there and result in real world consequences.
In this case, it was an emergency landing of a UAV trying to monitor compliance (or detect non-compliance) with a peace agreement. As we have shown in other
posts, the jamming in this area also impacts commercial airliners, ships and others.
The UN aviation and maritime organizations have both called GPS/GNSS jamming an urgent, safety of life issue.
No alt text provided for this image
Note that, even if the jamming also interferes with Russia's GLONASS satellite system, their forces still have access to
terrestrial Chayka (Loran-C) for
navigation and timing in that region.
Thanks to RNTF International Advisory Committee member Guy Buesnel for calling this report to our attention.
(May 2021) OSCE SMM Spot Report 13/2021: Emergency landing of long-range unmanned aerial vehicle due to dual GPS signal interference:
Format News and Press Release
Source OSCE
Posted 6 May 2021
On 6 May, the SMM was conducting an announced SMM long-range unmanned aerial vehicle
(UAV) flight. The UAV had taken off from its base in government-
controlled Stepanivka (54km north of Donetsk) at 12:30 and had immediately experienced dual
GPS signal interference, assessed as caused by jamming, which
then had occurred at intervals during the flight. At 16:01, while flying over areas near Kolosky (non-government-controlled, 46km south-east of
Donetsk),
the UAV had again experienced dual GPS signal interference, assessed as caused by jamming, which continued uninterrupted for the remainder of the flight.
Between 18:35 and 19:05, due to the risk of a loss of spatial control, the SMM had attempted three landings of the
UAV at its base in its Emergency Control
Mode, the first two of which had failed due to continuing dual GPS signal interference. On its third attempt, while dual GPS signal interference persisted,
the aircraft completed an emergency landing in a field about 600m north of its designated landing spot. The SMM retrieved the UAV and an initial assessment
did not reveal visible damage.
The Mission again highlights that since 21 March 2021 the SMM’s long-range
UAVs have been experiencing increased levels of GPS signal interference
on take-
off and landing, affecting both of their GPS receivers, in areas near their base in Stepanivka (See
SMM Spot Reports of 7 April 2021, 9 April 2021 and 24
April 2021). The Mission notes that, in each case, the source of GPS signal interference could have originated from anywhere within the radius of tens of
kilometres from the UAVs’ positions.
The SMM yet again notes that OSCE Permanent Council Decision No. 1117 specifies that the
SMM shall have safe and secure access throughout Ukraine.
Unrestricted and unconditional access to all areas is essential to ensure effective monitoring and reporting of the security situation, the ceasefire,
the withdrawal of weapons, demining, as well as disengagement. The mandate also tasks the Mission to report on any restrictions of its freedom of movement
or other impediments to fulfilment of its mandate.
These incidents hinder the Mission’s ability to conduct effective monitoring and reporting of the security situation in line with its mandate. Long-range
UAVs are an essential part of SMM operations, especially at night and in areas where the Mission’s monitoring and freedom of movement are restricted. While
the SMM cannot identify the precise source of jamming, it has observed the presence of jamming equipment on both sides of the contact line.
VIEW ORIGINAL REPORT: https://reliefweb.int/report/ukraine/osce-smm-spot-report-132021-emergency-landing-long-range-unmanned-aerial-vehicle-due
(May 2021) Satellite-navigation systems such as GPS are at risk of jamming, Alternatives are needed - The Economist:
Blog Editor's Note: This is a good general interest article to which we contributed. It is behind a paywall, so many of our readers may choose not to access
the entire piece.
Most significant is that a highly regarded journal is addressing the issue. A sure sign of the growth of widespread concern, and, hopefully, movement in many
quarters to mitigate risks.
Published on May 7, 2021
Dana A. Goward
President, Resilient Navigation & Timing Foundation; Proprietor, Maritime Governance, LLC
Blog Editor's Note: This is a good general interest article to which we contributed. It is behind a paywall, so many of our readers may choose not to access
the entire piece.
Most significant is that a highly regarded journal is addressing the issue. A sure sign of the growth of widespread concern, and, hopefully, movement in many
quarters to mitigate risks
5 May 2021
Back-ups for GPS
Satellite-navigation systems such as GPS are at risk of jamming Alternatives are needed
The phrase “critical infrastructure” conjures up solidly earthbound images: road and rail networks, water and sewage pipes, electricity grids, the internet,
and so on. Such stuff is so wound into the warp and weft of life that it is simultaneously both essential and taken for granted. One piece of infrastructure
which has become critical over recent decades, though, is anything but earthbound. This is the various constellations of satellites, the most familiar of
which is probably America’s Global Positioning System (gps), that orbit about 20,000km above Earth, broadcasting to the world precisely where they are and
exactly what time it is.
The original purpose of the GPS and its European (Galileo), Russian
(Glonass) and Chinese (BeiDou) counterparts was to enable suitably programmed receivers
on or near the ground to calculate their whereabouts to within a few centimetres, by comparing signals from several satellites. In this role they have become
ubiquitous, running everything from the navigation systems of planes, ships and automobiles, both military and civilian, to guiding the application of water
and fertiliser in precision agriculture. But global-navigation satellite systems
(GNSS), to give their collective name, now do much more than that. By acting
as clocks that broadcast the time accurate to within a few dozen nanoseconds, they are crucial to jobs ranging from coordinating electricity grids and
mobile-phone networks to time-stamping financial transactions and regulating the flow of information in and out of data
centres.
READ MORE (paywall ahead): https://www.economist.com/science-and-technology/2021/05/06/satellite-navigation-systems-such-as-gps-are-at-risk-of-jamming
(May 2021) In Fixing GPS, Timing is Everything - EE Times:
By George Leopold 04.26.2021
Global Navigation Satellite Systems, particularly the vulnerable U.S. Global Positioning System, represent a single point of failure that can be rendered
inoperable by unintentional or intentional inference. That reality, along with over-dependence on the nearly five-decade-old satellite constellation, has
forged a western consensus to accelerate development of terrestrial GPS backups and other mitigation strategies built around complementary position,
navigation and timing technologies.
Known in the industry as PNT, several federal agencies are working on demonstration projects aimed at testing and developing a terrestrial backup system
should GPS be knocked out by jamming, spoofing or interference aimed at the satellite constellation’s inherently weak signal.
READ MORE: https://www.eetimes.com/in-fixing-gps-timing-is-everything/#
(May 2021) Clear and Present Economic Danger - GW Prime:
Blog Editor's Note: An excellent article on Geospatial World Prime by RNTF Member Diana Furchtgott-Roth.
Diana is an economist who also led civil PNT issues for the US government, so she is uniquely qualified to examine this aspect of these issues.
Clear and Present Economic Danger:
Americans depend on GPS. While military dangers are obvious, outages would also cause incalculable damages to the economy.
By Diana Furchtgott-Roth
Former Deputy Assistant Secretary for Research and Technology | Department of Transportation; and
Adjunct Professor | George Washington University
Vadimir Putin’s Russia brags that his country’s new Pole-21 radio-electronic systems, soon to be installed in Siberia and the Ural Mountains, can spoof
America’s Global Positioning System (GPS), which provides positioning, navigation, and timing services through a system of satellites, and is vital to
Americans. Hacking it has never been easier.
Originally invented for the military, GPS was extended to civilian use by President Ronald Reagan in 1983 after the Russians downed a Korean Air Boeing 747
that had accidentally strayed into Soviet airspace, killing all 269 people on board, including Representative Larry McDonald, a Georgia Democrat.
GPS is increasingly open to hacking, as sophisticated technology has become cheaper and more widely available. In 2019, Iran spoofed the navigation system
of British tanker Stena Impero in the Strait of Hormuz. The ship’s crew thought they were in international waters when they were actually in Iranian
territory. The ship and its crew were held for 10 weeks by Iran.
READ MORE: https://www.gwprime.geospatialworld.net/special-feature/clear-and-present-economic-danger/
(May 2021) GPS Source Receives Order for 1,000th MAPS GEN I Assured Positioning, Navigation and Timing System:
COLORADO SPRINGS, Colo. – GPS Source, a subsidiary of General Dynamics Mission Systems and the only provider of a
currently fielded Assured Positioning,
Navigation and Timing (APNT) solution available to the U.S. Army, announced today it has received an order for the 1,000th
Mounted APNT System (MAPS),
Generation I (MAPS GEN I).
MAPS GEN I is a mobile modular system that monitors GPS signals for validity and sends the validated data to military devices, even when
GPS signals are
degraded or denied. This system has been in rapid development, production, and fielding since the
recognition of the critical need to protect GPS signals
against peer and near-peer adversary electronic warfare attacks. It is the only
mounted assured PNT solution allowing warfighters to conduct mobile
operations in a GPS-contested environment.
Read more: https://gdmissionsystems.com/articles/2021/05/11/news-release-gps-source-receives-u-s-army-order-for-1000th-maps-gen-1-apnt-system
(May 2021) Tech that guides you to the perfect parking spot, every time:
45% reduction in parking search time? Find out how cities around the world are reducing vehicle minutes traveled in this great article by
Gordon Feller
in Engineering360 #smartcity #smartparking #cleveryourcity
https://insights.globalspec.com/article/16606/tech-that-guides-you-to-the-perfect-parking-spot-every-time
Russia Tests Anti-Satellite Weapon, US Military Says:
By Rachel Jewett | July 24, 2020
U.S. Space Command reports it has evidence that Russia recently conducted an anti-satellite weapons test.
In a Thursday announcement, Space Command said Russia released a new object into orbit from Cosmos 2543 in proximity to another Russian
satellite. This is
similar to on-orbit activity conducted by Russia in 2017, and it is inconsistent with the system’s purpose as an inspector
satellite.
In February of this year, Space Command raised concerns about this same satellite system
when a Russian satellite maneuvered near a U.S. government satellite.
Then in April, military officials said that Russia tested a Direct-Ascent Anti-Satellite
(DA-ASAT) missile capable of destroying satellites in Low-Earth
Orbit (LEO). “This is further evidence of Russia’s continuing efforts to develop and test space-based systems, and
consistent with the Kremlin’s published
military doctrine to employ weapons that hold U.S. and allied space assets at
risk,” said Gen. John W. “Jay” Raymond, commander of U.S. Space Command and U.S.
Space Force Chief of Space Operations.
The Department of State, called the behavior “hypocritical and concerning.”
“This event highlights Russia’s hypocritical advocacy of outer space arms control, with which Moscow aims to restrict the capabilities of the United States
while clearly having no intention of halting its own counterspace program — both ground-based anti-satellite capabilities and what would appear to be actual
in-orbit anti-satellite weaponry,” said U.S. Assistant Secretary of State Dr. Christopher Ford.
(May 2021) Future-proof high-filtering antennas from Antcom build interference robustness and reject out-of-band signals:
https://antcom.com/about-us/press-releases/future-proof-high-filtering-antennas-from-antcom
(May 2021) If I Were King of the Forest: Resilient PNT for Critical Applications:
https://insidegnss.com/if-i-were-king-of-the-forest-resilient-pnt-for-critical-applications/
(May 2021) Adjacent Band Interference More than just a Ligado Problem - Spirent:
Blog Editor's Note: An interesting post by Guy Buesnel, a member of RNT Foundation's International Advisory
Committee. We have not often seen this issue
raised and appreciate his stimulating the discussion.
"While Ligado is the focus of the current controversy, it’s just one example of a problem that’s likely to grow as the world becomes more dependent on radio-based
services. The radio frequency (RF) spectrum is a finite resource, and fitting in new wireless services is increasingly difficult, with spectrum sharing between services
becoming commonplace.
As the spectrum gets more crowded, GNSS developers and users will likely have to contend with more sources of potential
ABI. That will require appropriate
countermeasures to be built into receiver designs, such as improved filtering of unwanted signals and improved shielding against signals transmitted at low
elevations."
Full disclosure, Guy is employed by Spirent which is an RNTF supporter, and
Spirent offers products and services to address interference with GPS/GNSS
signals.
Ligado Controversy Highlights Risk of Adjacent Band Interference to GPS Receivers
By:Guy Buesnel
May 11, 2021
Ligado’s 5G network is under fire again for potential interference with GPS. Users of
GNSS should assess the threats posed by adjacent band interference and
mitigate any risks.
The ongoing political conflict over US-based Ligado’s proposed 5G network has spilled over into the media, with
former deputy assistant transportation
secretary Diana Furchtgott-Roth highlighting the risks it poses to GPS in a fiery opinion column for the
Washington Post.
“Ligado’s signals will be 2 billion times as powerful as GPS signals,” she wrote on April 14th.
“Just as an outdoor rock concert would drown out birdsong,
the proposed Ligado 5G transmitters would overwhelm GPS signals.”
https://www.spirent.com/blogs/ligado-controversy-highlights-risk-of-adjacent-band-interference?
(May 2021) Dubins Path:
https://en.wikipedia.org/wiki/Dubins_path
(May 2021) Resilient PNT for Critical Applications - by Logan Scott:
Logan Scott
GNSS/GPS Expert
10 articles Following
There has been much discussion of the need for resilient PNT over the past few years as dependencies have grown and an evolving threat matrix has become
more active. As a nation, we need a measured and cost-effective response commensurate with the level of threats and the possible consequences.
What is resilience?
Do we even know what resilience is? Mostly it looks like extra cost when you don’t need it. Then, when it is needed and you don’t have it, it looks like
failure ---sort of like the Texas power grid back in February. Resilience has costs and budgets are bounded. My working definition for resilience is that
it is about building sufficiently secure and reliable systems out of insecure and unreliable components operating in an indeterminant environment.
How do you measure resilience? You try to break it and then decide whether the protection is adequate for the domain of use.
Any system will break under
sufficient stress. Determining what is sufficient is a hard question but it is a key question. Resilience could end up being quantified using a series of
tests like UL standards for safes. You expose the safe to a skilled safecracker and see how long it takes them to break in. Interestingly, the highest
security rating, TXTL-60, only guarantees protection for 60 minutes.
The need for standards and mandates.
READ MORE: 10 articles Follow:
There has been much discussion of the need for resilient PNT over the past few years as dependencies have grown and an evolving threat matrix has become
more active. As a nation, we need a measured and cost-effective response commensurate with the level of threats and the possible consequences.
What is resilience?
Do we even know what resilience is? Mostly it looks like extra cost when you don’t need it. Then, when it is needed and you don’t have it, it looks like
failure ---sort of like the Texas power grid back in February. Resilience has costs and budgets are bounded. My working definition for resilience is that
it is about building sufficiently secure and reliable systems out of insecure and unreliable components operating in an indeterminant environment.
How do you measure resilience? You try to break it and then decide whether the protection is adequate for the domain of use. Any system will break under
sufficient stress. Determining what is sufficient is a hard question but it is a key question. Resilience could end up being quantified using a series of
tests like UL standards for safes. You expose the safe to a skilled safecracker and see how long it takes them to break in. Interestingly, the highest
security rating, TXTL-60, only guarantees protection for 60 minutes.
The need for standards and mandates.
A core question we have not addressed at a national policy level is how to incentivize resilience. When seat belts were invented, they were made available
as an option by Ford and others. It was not a popular option. Less than 2% of buyers elected to get them. Then, through a series of federal mandates, they
became required equipment and later, we saw requirements to use them. The point being that safety standards are needed, they have costs, and, if they are
left optional, they may not be implemented or used.
I like that DHS is addressing resiliency as a risk management question but leaving the implementation of protections entirely up to the user community
strikes me as unworkable. Our user communities are rarely aware of the potential risks, much less how to address them. Even when they are aware of the
risks, industry is often more driven by cost considerations under nominal conditions, and they fail to prepare. I’ll pick on the Texas power grid in
February again, but I could also have picked on “just in time” manufacturing systems vulnerable to supply chain disruptions, or the Suez Canal. By
establishing standards and exposure-based testing procedures, vendors and buyers in critical infrastructure domains can avoid the more egregious outcomes
in a cost-effective manner.
The need for Modular Open Systems Approaches (MOSA)
In prior discussions I have noted that building a resilient architecture is not just about having the right parts; they must be integrated correctly (and
tested). MOSA is about effectively leveraging the capabilities of diverse system components and maintaining currency as new innovations and technologies
become available. MOSA is a platform, it is an operating system, it is an enabler.
It is not a point solution.
A cell phone’s positioning process is a great example of MOSA. Android phones come in diverse flavors and have a rapid innovation cycle based on a rich and
constantly evolving ecosystem of parts. Yet, they all manage to integrate sensors together to establish position with good accuracy both indoors and
outdoors. That said, cellphones performed abysmally when exposed to inadvertent spoofing at the
ION GNSS+ conference in 2017.
In many ways, integrity and resilience are highly intertwined problems and so, there are opportunities within
MOSA constructs to approach the problem of
safely integrating less than 100% trusted, 100% reliable components. Experience with cybersecurity shows the need for a rapid update and response cycle—MOSA
will help.
The need for authentication
Authentication is about knowing where your data comes from, knowing where your software comes from, and establishing a chain of evidence to establish
provenance. In the MOSA paradigm, if subsystems can report problems due to spoofing, jamming, cyberattack, hardware failure, software corruption etc.
AND, there are performance and security monitors in place to aggregate information and watch for discrepancies, a more effective and resilient response
can be mounted. OS-NMA and Chimera can help by providing unambiguous discrepancy reports. Depending on the operating domain, it may even be possible to
report problems to higher authorities so as to establish patterns and causes. For instance, jamming might be rapidly geolocated using crowdsourcing methods
ala. J911 but such an approach is viable only if you can establish trust in your
sources.
The need for trustable multi-GNSS
In the quest for resilience and augmentations, I am not convinced that we as a nation have fully explored how to safely integrate foreign navigation
systems into critical applications. Access to more signals and more systems offers considerable resilience potential. Instead, the
FCC has unilaterally
restricted their use under part 25 rules with limited justification. Perversely, this has led to some US companies flying their satellites under foreign
flags so as to gain legal access to FCC proscribed navigation signals. These same restrictions limit the performance of precision positioning systems,
receiver autonomous integrity algorithms, positive train control systems, and, spoofing detection processes.
One of the things I found fascinating about the Galileo failure in July 2019 was that the satellites all continued to produce good ranging signals. If you
could provide your own ephemeris, say from JPL, NASA, NSWC, and/or other sources, you still got great performance. Treating foreign navigation satellites
as “signals of opportunity” and using curated and signed US generated ephemeris strikes me as a useful augmentation. Much less trust is placed in the
foreign state, yet you get a lot of augmentation benefit for minimal cost. Additionally, you limit the impact of a global system’s outage. If
Galileo had
been the only game in town, its one-week outage would have been catastrophic. As it was, its absence was noted but had almost no effect on
GNSS dependent
operations.
The need for an honest evaluation of Ligado’s impact on
GNSS really is different from communications. The FCC, by setting a standard where the mechanism of harm is to place
GNSS receivers in deep and uncontrolled
saturation, ignores the possibility of normally harmless signals mixing and causing harm. None of the testing to date has explored this issue and so, our
national policy might be the RF equivalent of "mixing alcohol and fentanyl and hoping for the
best". Furthermore, the FCC showed almost no cognizance of the
importance of GNSS based remote sensing in monitoring climate change. The RF smog that Ligado’s signals will create restrict our ability to develop a clearer picture
of what is happening. The FCC’s decision needs to be revisited using sound engineering as a basis.
Augmentations and the role of markets
One of the most insidious things about GNSS is its price to the user: FREE. That, combined with its worldwide coverage and superb accuracy in both time and
positioning creates significant barriers to entry for new offerings. In the commercial arena, a new entry that provides only the same services as GNSS,
maybe a little better, seems doomed. A successful entrant will need to have a value-added proposition with features that cannot be met using GNSS.
Communications facilities, indoor operation, proof of integrity and location, and uninterruptable service would all be on my short list. In large measure,
these capabilities can be provided by combining GNSS with other sensors and systems especially if we use the full constellation of 125 navigation satellites
on orbit and healthy now. That said, I do expect new entrants.
5G NR and 802.11 both have strong potential to meet the requirements of my short list, especially as they move towards higher frequencies. Yes, the ranges
there will be short, but densities will be high. Both technologies have strong and active initiatives within their standards setting process oriented
towards providing accurate, high integrity positioning. Also, because they are extant systems, there is less pressure to offer ubiquitous service at
inception, a daunting challenge for a brand new entrant.
I expect LEO satellite systems will also have a role. Because they have high angular rates across the sky, you can get nearly instant on cm level
positioning. Operating at higher frequencies, eg. X, Ku or even V-band, they can simultaneously provide strong communications capabilities when outdoors
and so, might play very well in the autonomous vehicle markets. Yes, the antenna issues are challenging, but they ride a wave of actual deployments.
The role of government
So, what is the proper role for government? Well first, stably fund, maintain, and operate
GPS. It is critical infrastructure, not easily supplanted.
Providing secure ephemeris and integrity data to support safe use of multi GNSS should be funded. Of course, removing
FCC roadblocks to its use is also
essential. PPP data services should be considered as part of the package to promote rapid adoption of “safe ephemeris”.
Beyond that, government’s role should be one of dare I say it, leadership. Defining what we want for resilience and what standards of performance are
needed in critical applications is only part of the solution. We also need to take action to ensure these standards are met by introducing clear
requirements and ensuring necessary infrastructure is available. Developing an integrated infrastructure plan that uses
GEO, MEO, LEO and terrestrial
components to our best advantage is a necessary step. Government needs to influence approaches not only as a provider of public infrastructure but as
a customer for private infrastructure. Resilience is best achieved as a cooperative undertaking with industry but absent leadership, nothing is going
to happen. Until it does.
Important Comment by Grant Taylor:
The role for government is by most important part of any new PNT technology rollout, as any service will need to be public accessible, like what
GPS is.
This is where I am running into dead ends with my ground based PNT system, as open access and a standard business model simply do not go together. The
only way to provide alternatives to GPS, would be through public private partnerships, where private enterprises could support new technology and have
setup / operating costs reimbursed by the government. This may work here in Canada, but would be a major issue to overcome within the
US, where government
and private enterprises working together are viewed as a bad thing. (Just look at healthcare systems as an example.)
---------------------------------------------------------------------------------------------------------------------------
https://www.linkedin.com/pulse/complementary-pnt-demonstration-logan-scott/
---------------------------------------------------------------------------------------------------------------------------
https://www.linkedin.com/pulse/observation-using-foreign-gnss-critical-applications-logan-scott/
----------------------------------------------------------------------------------------------------------------------------
EU Draft Adjacent Band Interference Specification is Available (ETSI EN 303 413 V1.1.0):
https://www.linkedin.com/pulse/eu-draft-adjacent-band-specification-available-logan-scott/
----------------------------------------------------------------------------------------------------------------------------
https://www.linkedin.com/pulse/what-potential-low-earth-orbit-constellations-augment-logan-scott/
(May 2021) New Liquid Coating Could Make Stealth Aircraft Invisible and Hypersonic - The Debrief:
"In an attempt to improve on current materials, which notoriously have several drawbacks, a team from the North Carolina State University has developed a
new ceramic-based coating that not only offers dramatic improvements in radar invisibility but will likely result in a whole host of improvements to the
aircraft’s overall performance."
https://thedebrief.org/new-liquid-coating-could-make-stealth-aircraft-invisible-and-hypersonic/
(May 2021) What are Global Navigation Satellite Systems (#GNSS) and how do they support position, navigation and timing (#PNT) applications:
across the world?
Learn how GNSS were developed and how they enable the work we do around the world >>
https://hxgn.biz/3hBRs1E
https://novatel.com/tech-talk/an-introduction-to-gnss/what-are-global-navigation-satellite-systems-gnss:
(May 2021) Don't Just Bail Out Uncle Sam, Help Ordinary Americans Too - Real Clear Markets (Ligado issue):
Blog Editor's Note: Another great piece by RNT Foundation member, Diana
Furchtgott-Roth. She makes the point that in its decision to approve Ligado's
application, the FCC required the company to reimburse the U.S. government for any harm done to its equipment and systems. But what about the rest of us?
Right on, Diana!
Don't Just Bail Out Uncle Sam, Help Ordinary Americans Too
By Diana Furchtgott-Roth
The cyberattack on the Colonial Pipeline has increased awareness of the fragility of infrastructure. It should also serve as a reminder to policymakers of
a very real threat to the Global Positioning System, and of an ill-advised decision that protects government users from having to foot the bill when their
GPS receivers are affected--while ignoring ordinary Americans and industries.
The risk comes from an April 2020 Federal Communications Commission order granting an application from
Ligado Networks to operate a terrestrial network
using spectrum next to the bands reserved for GPS. And while the FCC’s order acknowledged the risk
by requiring Ligado to pay for damages to federal
devices, it does not require the company to compensate individuals and
companies, such as pipelines, helicopter terrain awareness warning systems, car
navigation systems, and power plants -- costs that could run into the tens of billions of
dollars.
READ MORE: https://www.realclearmarkets.com/articles/2021/05/20/dont_just_bail_out_uncle_sam_help_ordinary_americans_too_777973.html
(May 2021) MDA Holds Briefing on FY22 Defense Budget:
Navy Vice Adm. Jon A. Hill, director, Missile Defense Agency, and Michelle C. Atkinson, director for operations briefs the news media on
President Joe
Biden’s fiscal 2022 defense budget, May 28, 2021.
https://www.defense.gov/Watch/Video/videoid/799271/dvpcc/false/#DVIDSVideoPlayer581
Focused on MDA: https://www.defense.gov/Watch/Video/videoid/799271/dvpcc/false/#DVIDSVideoPlayer581
(June 2021) Special issue of ACM: History of MatLab:
https://dl.acm.org/toc/pacmpl/2020/4/HOPL
(May 2021) Startling GAO Report on DOD Navigation - Webinar June 15th:
The General Accountability Office (GAO) released a somewhat scathing report about Department of Defense navigation programs this month.
Among their findings and inferences were:
Navigation requirements for projects and systems are often overstated with managers just defaulting to
GPS accuracy requirements
Resilience is not a requirement for navigation systems in many cases
Alternate (non-GPS) navigation systems are not a priority for the department, and are actively opposed in some instances
There is a lack of coordination across the department on alternate PNT systemsThe Institute of Navigation and the RNT Foundation will hose a webinar on the
15th of June featuring two of the report's authors.
Attendance is open to the public and free, but advance registration is required.
REGISTER HERE: https://www.ion.org/publications/webinars.cfm
(May 2021) Northrop Grumman to supply navigation payloads for DARPA’s Blackjack satellites - Space News:
https://www.linkedin.com/pulse/northrop-grumman-supply-navigation-payloads-darpas-blackjack-goward/?trackingId=hnfXwTC%2FvYFETbTOJOcQ4w%3D%3D
https://spacenews.com/northrop-grumman-to-supply-navigation-payloads-for-darpas-blackjack-satellites/
(May 2021) Weighing the Costs of GPS Disruption and Developing Backup Capabilities:
GPS signals are susceptible to both unintentional and intentional disruption, leaving critical infrastructure vulnerable. But how do the costs of a
potential GPS backup compare to the threats that such a backup would mitigate?
https://www.rand.org/pubs/research_reports/RR2970.html?utm_campaign=&utm_content=1622395980&utm_medium=rand_social&utm_source=linkedin
https://www.rand.org/pubs/research_reports/RR2970.html
(June 2021) New GAJT Protects Against RF Interference and Jamming in Marine Environments - Defense Advancement:
The new GAJT-410MS from Hexagon | NovAtel is the latest in GPS
Anti-Jam Technology (GAJT) that will provide interference mitigation and jammer
direction-finding for advanced situational awareness in marine environments.
The GAJT-410MS provides dynamic protection on both GPS L1 and
L2 bands, as well as Galileo E1, QZSS
L1 and L2 and SBAS L1 to combat intentional
and unintentional interference.
For more information:
https://www.defenseadvancement.com/news/new-gajt-protects-against-rf-interference-and-jamming-in-marine-environments/
(June 2021) $17M proposed for DOT resilient PNT initiatives - GPS World:
$17M proposed for DOT resilient PNT initiatives
June 4, 2021 - By Dana Goward
Office and Management and Budget (OMB) seeks to extend Trump policies and repeal timing law counter to its own study and industry input
The Biden administration’s budget proposal delivered to Congress last week includes $17 million for the small
Department of Transportation (DOT) office
responsible for leading civil positioning, navigation and timing
(PNT) efforts for the nation. This is a marked increase over the $2 million allocated in
2020 and estimated $5 million being spent this fiscal year.
At the same time, it seeks to repeal the National Timing Resilience and
Security Act of 2018 that mandated DOT establish a terrestrial timing
backup for GPS.
This, despite the findings of a recently published RAND study completed for the
Department of Homeland Security (DHS), and other input from a
telecommunications industry group.
Proposed Spending
The administration’s budget proposes $17 million for the DOT Office of Research and Technology to be
split among three areas of effort.
Monitoring and detection. The first is a $3.5 million “(GNSS) performance monitoring and interference detection”
project. This is a one-time request that is
expected to be followed by a request for $1 million in yearly funding to maintain and operate the capability.
While these may not seem like sufficient funds to many, DOT is tasked with working with other departments and agencies, and to leverage existing
capabilities. The National Geospatial-Intelligence Agency (NGA) is specifically named as an important partner with
DOT in this effort. NGA already has
responsibility for issuing worldwide navigation warnings for U.S. interests. It also has access to a wide variety of information that could be used for
the project.
Signal authentication. Another $3.5 million is proposed for Executive Order
(EO) 13905 Implementation and GPS Signal Authentication. The EO was issued in
February 2020. It seeks to leverage market forces and education to create additional sources of
PNT and encourage users to access them. This approach has
been criticized by many as unworkable without extensive regulation and mandates for users, while still not addressing the majority of American companies
and users.
$1.5 million of this $3.5 million will go to further implement the EO through development of a
“PNT threat space model” and otherwise support inter-
department PNT profile and research and development efforts.
$2 million would be allocated for a one-time investment in GPS signal authentication to “result in the development and validation of requirements for
data and signal authentication capability for civil GPS,” reads the proposal.
DOT has regularly requested much greater sums to establish civil signal
monitoring, leading many to believe the requirements are already well known. One industry observer suggested this could be “a study in lieu of action.”
GPS Backup. $10 million would be spent for “GPS Backup/Complementary PNT Technologies Research,” essentially follow-on studies to the
DOT GPS
Backup Technologies Demonstration. “These efforts will further develop
PNT modeling, simulation, and testing tools, as well as
standards and
performance monitoring tools needed to evaluate integration of diverse
positioning, navigation, and/or timing technologies into end-user applications.
This work will also support development of cyber-secure receivers,” reads the proposal.
Proposed Repeal of Timing Law
More surprising to many than the significant increase in proposed funding is inclusion of a proposal to repeal the
National Timing Resilience and Security
Act of 2018 (NTRSA).
One congressional staff member expressed shock at seeing that provision. “The act was the epitome of thoughtful, bipartisan congressional effort,” the
staff member said. “It was co-sponsored in the Senate by Markey and Cruz, for crying out loud. You can’t get more bipartisan than that. To have this dumped
on us without any notice or consultation is amazing. It is not something I would expect from this White House. I am not sure how serious a proposal it is.”
Some observers on the hill and elsewhere have opined that, rather than the repeal proposal being a well-vetted administration policy, it is an effort by
OMB staff held over from the previous administration to carry forward and preserve President Turmp’s Executive Order 13905 and other
PNT policies.
Rather than focusing on establishing a GPS backup capability; they, instead,
urged PNT users to find and pay for alternatives on their own.
Harsh Tone, False Assertions
Compounding the surprise is the exceptionally harsh tone in the proposal, and
assertions that many claim are outright false.
Among the problems with the language seen by observers is its assertion that NTRSA
seeks to establish a single backup for GPS services.
“It’s unclear to me where such an assertion is supported in the record,” said Greg Winfree,
former Assistant Secretary at DOT in the Obama administration.
“NTRSA requires the department to incorporate findings from the GPS back-up demonstration program. That project
found a variety of systems are
needed to protect America,” he said. “NTRSA does require establishment of at least one system, which is incredibly
important. Without at least one
alternative in place, GPS is one of highest priority targets for our
enemies. We have to get the bullseye off of GPS. NTRSA does that.”
This point on national security was reinforced by Scott Pace, head of the Space Policy Institute at
George Washington University (GWU). Pace was executive
director for the Space Council in the Trump administration. At a recent GWU webinar on the
topic, he commented that having an alternative to GPS will
contribute to national security and improve global stability. It will “lower the pressure on us to escalate and respond” should
GPS satellites be damaged,
or services disrupted, he said.
China, Russia, and other nations have terrestrial PNT alternatives to GNSS already in operation.
This imbalance creates strategic and tactical problems
for the United States, according to many analysts.
The proposed budget also describes NTRSA’s goal of providing at least one backup as “inefficient, anti-competitive and potentially harmful to the existing
market for back-up/complementary PNT services.”
“Exactly the opposite is true,” according to Diana Furchtgott-Roth, GWU economics
professor. Until January of this year, she led civil PNT issues within
the Trump administration as a Deputy Assistant Secretary for Research and Technology at
DOT. “DOT’s Complementary PNT and GPS Backup
Technologies Demonstration Report, published in January, specifically stated that
a variety of technologies are needed to complement GPS. What is the most
cost-efficient in an urban area is not necessarily the most cost-efficient in a rural or maritime
area.”
“PNT is a utility used by every American. Having affordable complementary service available to people in rural and urban areas is the height of efficiency.
It is unquestionably in the interests of national and economic security. In fact, access to at least one alternative should be free so to encourage
adoption and best protect the nation,” she said.
“GPS is now a free service provided by the government, and the government is responsible for making sure that it is reliable. GPS outages would cause
harm across a broad range of economic activities, including emergency services, general aviation, pipelines, and the electricity
grid,” according to
Furchtgott-Roth.
Not-So-New and Contradictory Research:
The proposal to repeal NTRSA cites “recent federal analyses” as part of its justification. One of these is likely a report done for the
Department of
Homeland Security (DHS) by the RAND Corporation. Touted in a press release last month as “new research” and labeled “Published 2021,”
the work was actually
completed in 2019. DHS representatives have said the delay in publication was needed for review and approval.
Yet the report was the basis for a DHS report to Congress submitted in April 2020. This has caused some to opine that
its publication was timed to
reinforce OMB’s effort to repeal NTRSA. “You don’t submit reports to Congress based on un-reviewed, un-approved material,” said a retired
DHS official.
"The timing of its release is clearly deliberate.”
The study, “Analyzing a More Resilient National Positioning, Navigation, and Timing Capability,” takes a cost-benefit approach to the issue.
One of its
high-level findings is that government investment in a duplicate, GPS-like backup capability is not warranted.
At the same time, it found that government investment in a national timing network, such as the one mandated by the
NTRSA, is likely warranted. Saying
that a complete backup for all GPS services in all parts of the country is not
cost-beneficial, the study says there are some “…federal initiatives that
do appear to be cost effective or close to cost effective.” These include “Timing-only backup through fiber/FirstNet, eLoran, or STL [Satelles].”
According to the retired DHS official, this directly contradicts OMB’s assertion that NTRSA should be repealed. “Either they didn’t read the whole thing,
or they counted on most people not reading farther than the top-level recommendations,” he said. “And those
top recommendations were clearly selected to
match OMB’s desired outcome.”
Telecommunications Industry Cites Need for NTRSA Provisions:
The May 2021 “Report to the President on Communications Resiliency” also runs counter to claims made in the budget proposal. In it, the president’s
National Security Telecommunications Advisory Committee (coordinated by
DHS) cites the need for GPS alternatives in telecommunications and urges
President Biden to fund them. It specifically mentions the need for a national timing
architecture, and cites the provisions of NTRSA several times as a step
in the right direction.
The industry group Alliance for Telecommunications Solutions also sent letters in May to congressional leaders urging funding for GPS
alternatives.
Continuing the Discussion:
Congress has become increasingly dissatisfied with executive branch actions on resilient PNT over the last decade.
The most recent evidence of this is an extensive and highly critical report of the Department of Defense’s approach to PNT resilience released May 10 by
the Government Accountability Office (GAO). Among its recommendations was to not rely on GPS as a primary PNT source but
look to more resilient technologies.
While President Trump’s 2020 Executive Order did not make precisely the same recommendation to civil
users, it did focus on “responsible use” of PNT
and transitioning to using additional, non-GPS dependent sources.
The question still under discussion is how far the government should go to support such a transition.
Seasoned observers regularly comment that Congress has the “power of the purse” and
every president’s budget is “dead on arrival” regardless of which
party controls the White House.
It seems clear that resilient PNT will be a topic of lively debate between the Congress and the White
House, as well as internally on the hill, for the
foreseeable future.
(June 2021) "The Russia Trap" - Single Points of Failure & GPS:
Blog Editor's Note: We were interested to find the discussion of the importance of resilience and PNT in
George Beebe's book "The Russia Trap."
Beebe talks about "War by Other Means" and how simmering tensions can cause seemingly innocuous interactions to spiral out of control. Hence the
"trap" potentially leading to an otherwise unthinkable nuclear war.
One of the key strategies to avoid this, he says, is the ability for America to "absorb shocks,"
by which he means "resilience." The ability to
resist disruption as much as possible, and when not possible to minimize the disruption...
He starts his chapter "Absorbing Shocks" by pointing out that we have shock absorbers on our cars because we know that, despite the best efforts
of highway departments, there are always going to be bumps in the road. Shock absorbers aren't there to "correct these defects, but to make them
less damaging to vehicles and less painful to drivers and passengers."
Beebe discusses several areas in which America is significantly
under-resilient. His discussion of technological resilience is pertinent to on-going
discussions in the PNT world.
THE RUSSIA TRAP:
How Our Shadow War with Russia Could Spiral into Nuclear Catastrophe
TECHNOLOGICAL RESILIENCE
Part of designing resilience into the system involves identifying critical "single points of failure"
features and building backups that can
compensate for their damage or loss. As processes that were once performed by humans have increasingly grown more
automated, we have realized
stunning efficiencies...
These systems are not only vulnerable to cyber-interference from Russia and a range of other state-sponsored and individual cyber-actors but
also
to extreme weather events...
The American Global Positioning System (GPS) is but one example of a system upon which numerous critical military and commercial functions depend,
but which is highly vulnerable to disruption and at present is not adequately backed up by emergency alternative systems. Plans have recently been
put in place to provide such a backup, but they have been moving slowly. Most experts agree that the
"eLORAN" system (Enhanced Long-Range Aids to
Navigation), developed by the US Coast Guard, can provide an effective non-GPS-dependent timing and navigation system that can sustain critical
national communications and other GPS-related functions in the event of a sustained outage...
But discussions about the need for a backup system have been underway for nearly twenty
years, and even now the new legislation makes implementation
"subject to the availability of appropriations." The pace of progress has lagged vastly behind the urgency of the
problem.
Blog Editor's additional note: eLoran has been identified by multiple government studies and
twice been recommended by the US National Space-based
Positioning, Navigation, and Timing Advisory Board. It was also one of several technologies in the
Department of Transportation GPS Backup Technology
Demonstration. The resulting report said multiple systems were needed to adequately "backup"
GPS. Also that, based on the demonstrations, L-band signals
from space, Low Frequency, and UHF signals were
needed, and that the terrestrial transmitters should be connected by
fiber. eLoran is one of several Low
Frequency systems that could be employed.
(June 2021) This, from an excellent deep dive by RAND on the resilience of US Positioning, Navigation, and Timing capabilities:
https://buff.ly/3uXFdzt
See this gentle rebuttle by Dana A. Gowerd:
Hi Brian,
The high level conclusions are, I think, misleading for policy makers. The study actually says that backing up
GPS timing is likely worthwhile, as is backing up positioning
in limited areas..
The study was completed in 2019 to support a Trump administration report to Congress (sent in April 2020) opposing a law and other congressional efforts to get them
to establish a timing backup for GPS.
Likely why the "backing up GPS not worth it" was highlighted and "backing up timing everywhere and positioning in some areas" was
NOT.
Not sure why DHS and OMB want to keep America vulnerable/weak relative to China, Russia, & Iran in our ability to withstand disruptions to
GNSS signals.
The "cost-benefit" approach also ignored strategic issues like our overall resilience and the need to "take the bullseye off of
GPS" as one of the most attractive targets
for our adversaries.
See https://www.gpsworld.com/17m-proposed-for-dot-resilient-pnt-initiatives/
(June 2021) Air Force Gen. John W. Raymond: Chinese lasers, jammers threaten GPS satellites - The Washington Times:
Blog Editor's Note: We have talked a lot in recent posts about the PNT gap between the
U.S.A. and our adversaries China, Russia, and Iran. It is a gap that,
as Beebe says in "The Russia Trap" (could also be titled "the China
Trap") creates conditions that could easily spiral us into nuclear war.
Think that claim is a bit "out there"? A single bullet started WWI. - But, we are so much smarter now...
NOT! - Read the book before you decide. And consider
the comments we have reported from former Obama and Trump administration officials along the same lines.
US policy is that if anyone messes with our critical space assets the nation will mount "...a deliberate response at a time, place, manner, and domain of its
choosing..."
Concerns expressed by Beebe and others are that, if when GPS is interfered with the
US has no fallback capability, such a response will necessarily be
harsher, more provocative, and more likely to lead to an escalating conflict.
While serving officials are unlikely to comment in such a way, they do regularly comment on threats and
vulnerabilities. We need to understand these reports
in the larger context of great power competition.
The below report is yet another four star trying to signal civilian leadership that
we "really have a problem here."
Air Force Gen. John W. Raymond: Chinese lasers, jammers threaten GPS satellites
By Bill Gertz - The Washington Times - Monday, May 10, 2021
China’s space weapons include missiles and killer satellites, but Beijing’s
most worrying arms are lasers and electronic jammers capable of destroying or
disrupting Global Positioning System navigation satellites used by the U.S.
military, the general in charge of space says.
READ MORE: https://www.washingtontimes.com/news/2021/may/10/air-force-gen-john-w-raymond-chinese-lasers-jammer/
(June 2021) GMV awarded contract for Galileo HAS data generator - GPS World:
GMV has been awarded a contract for the implementation of the Galileo High
Accuracy data generator (HADG):
https://www.gpsworld.com/gmv-awarded-contract-for-galileo-has-data-generator/
(June 2021) Robust, credible and layered missile defense is the foundation of deterrence:
https://www.defensenews.com/opinion/commentary/2021/06/16/robust-credible-and-layered-missile-defense-is-the-foundation-of-deterrence/
(June 2021) Let the Coast Guard Operate eLoran - US Naval Institute Proceedings:
Blog Editor's Note: Up front caveat - the editor has deep Coast Guard experience and more that a passing familiarity with eLoran. In fact, he probably
still is on the "bad list" of a major telecommunications company because he was not able to arrange a two month delay of the 2010 shutdown of Loran-C in
the U.S. The company had been using it as a timing reference.
That said, eLoran has been regularly recommended as a complement to GPS by government studies and the national PNT advisory
board. And Loran is in
operation elsewhere in the world. So, if it was part of the suite of solutions the US adopted, it would provide opportunities for constructive engagement with others.
And we know at least one senior Capitol Hill staff member who thinks that having the Coast Guard resume this duty is the way to go.
A good article. We particularly like the sidebar "The Dangerous Radio-Navigation Capability Gap." This is a point that seems to have been missed by many
policy makers, though it is being discussed more recently. See our recent post on
"The Russia Trap" and the comments of officials from the Obama and Trump
administrations in this article.
Let the Coast Guard Operate eLORAN
The United States must address its GPS capability gap, and the Coast Guard’s expertise makes it the right service to lead the way.
By Ensign David W. Zenkel, U.S. Coast Guard
June 2021Proceedings
https://www.usni.org/magazines/proceedings/2021/june
(June 2021) Cybersecurity Experts Push President Biden To Protect GPS Satellites And The Connected Car - Forbes:
Blog Editor's Note: Great article with some interesting background. And more widely applicable. Just remove
"connected car" from the title and substitute,
well... just about anything, and it should still work. "President Biden, we urge you to protect GPS satellites and the... electrical grid... the network...
delivery services..." - you name it.
In truth, though, a lot of the easiest fill-in-the-blanks are transportation
related. That's why DOT has long had the rose pinned on them for civil
PNT.
And yes, as is reported in this article, PNT is infrastructure! Critical infrastructure! -
Can someone in government say that out loud, please?
May 18, 2021,07:10am EDT|
Cybersecurity Experts Push President Biden To Protect GPS Satellites And The Connected Car
Steve Tengler, Senior Contributor on Transportation
Sometimes when you exclaim the sky is unprotected, they mentally label you as Chicken Little and ignore your alarms. Or sometimes they might believe your
warnings yet quietly follow the group inertia that’s the cornerstone of
groupthink..
Such is the tale of Lisa Donnan, an internationally recognized expert in cybersecurity and operating partner at Option3 Ventures, and Julian Gresser, the
former advisor to the U.S. State Department and World Bank and co-founder of The Balance Group. They have vigorously waved the Caution Flag regarding an
insecure, trusted, non-critical infrastructure (satellites) communicating to a trusting non-critical infrastructure (vehicles) that could disrupt a vast
network of highways, bridges and tunnels that are recognized as critical infrastructure.
READ MORE: https://www-forbes-com.cdn.ampproject.org/c/s/www.forbes.com/sites/stevetengler/2021/05/18/cybersecurity-experts-push-president-biden-to-protect-gps-satellites-and-the-connected-car/amp/
(June 2021) New Algorithm Helps Autonomous Vehicles Find Themselves, Summer or Winter:
A new Science Robotics paper https://lnkd.in/g8mV8dP
on Learning based Visual Terrain-Relative Navigation was published today. Tony Fragoso, Connor Lee,
Austin McCoy. Funded by Boeing, National Science Foundation
(NSF), and Caltech.
https://www.caltech.edu/about/news/new-algorithm-helps-autonomous-vehicles-find-themselves-summer-or-winter
(June 2021) U.S. government prepares to issue landmark report on UFOs:
The U.S. government, once openly dismissive of UFO sightings that for decades sparked the popular imagination, is poised to issue an expansive account of what it
calls "unidentified aerial phenomena" based heavily on observations by American military pilots.
https://lnkd.in/ebaBQhF
https://www.reuters.com/world/us/us-government-prepares-issue-landmark-report-ufos-2021-06-24/
----------------------------------------------------------------------------------------------A
Criticism:
James Kiessling, 1st degree connection
Systems architect and analyst
Gads - observations by pilots - that's lovely - an unimpeachable source since their ego's cannot admit that training to fly does not make you an excellent
observer or expert at artifacts that onboard sensors can create. Having actually analyzed some of the source data - I expect that with time, at least 70%
of the cases - certainly over 85% where recorded data is available can be explained. I am far more interested in the story from:
https://www.thedrive.com/the-war-zone/40054/adversary-drones-are-spying-on-the-u-s-and-the-pentagon-acts-like-theyre-ufos
(June 2021) Extremely accurate time is increasingly critical. This place is in charge of it. - National Geographic:
Blog Editor's Note: Interesting article about the UK's capabilities. Also timely since we just did a webinar last week, in partnership
with Hoptroff, on timing in the UK with Leon Lobo of the National Physical Laboratory. Look for the recording of the webinar to be posted soon.
In the U.S. our timekeepers are the National Institutes of Standards in Boulder,
CO, and the U.S. Naval Observatory in Washington, DC.
And at the risk of repeating the message too many times we will remind everyone that, not only is timing important, it also has to get
to folks so they can use it. Establishment of a national timing system to backup GPS has bee the subject of recommendations in the U.S.
for years, including:
The National Security Telecommunications Advisory Committee
(NSTAC), a government board of major telecom CEOs and executives, recommended
to President Biden in May that he fund a National Timing Architecture.
The US National Space-based PNT Advisory Board recommended a terrestrial timing backup for GPS
The Alliance for Telecommunications Industry Solutions (ATIS)
wrote to senior members of Congress urging them to invest in a national
timing system. PNT Foundation published a white paper in October 2020 entitled
"A Resilient National Timing Architecture"
A recently released report for DHS by RAND found that federal investment in a timing system is likely worthwhile.
The UK is moving forward, China, Russia, Iran, and South Korea are
already there. Where is the US?
If you've ever been mystified by the term 'atomic clock,' or wondered what quartz has to do with time, this is the lab with the answers:
By Dominic Bliss
Teddington, on the southwestern edge of London, is home to three of the most precise clocks on the planet.
They are accurate to one billionth
of a second per year. So accurate, in fact, that for them to lose or gain just one second, they would need to keep ticking for the next 14 billion
years; until the end of the universe. Bear that in mind when you’re next changing the batteries in your wristwatch.
These clocks, housed inside the UK’s National Metrology Institute – the centre responsible for developing an maintaining measurement standards and
itself located at the National Physical Laboratory – are known as optical atomic clocks, and they’re more accurate even than the previous generation
of cesium atomic clocks. Of course they bear no resemblance whatsoever to any timepiece you might wear on your wrist or set atop your mantelpiece.
There are no hands or clock faces or spinning wheels or any of that mundane horology.
READ MORE:
https://www-nationalgeographic-co-uk.cdn.ampproject.org/c/s/www.nationalgeographic.co.uk/science-and-technology/2021/06/keeping-extremely-accurate-time-
is-a-matter-of-supreme-national-importance-and-this-is-the-place-that-keeps-it/amp
(June 2021) Quantum random number generator sets benchmark for size, performance:
As pervasive as they are in everyday uses, like encryption and security, randomly generated digital numbers are seldom truly random. So far,
only bulky, relatively slow quantum random number generators
(QRNGs) can achieve levels of randomness on par with the basic laws of quantum
physics, but researchers are looking to make these devices faster and more portable. In Applied Physics Letters, by AIP Publishing,
scientists
from China present the fastest real-time QRNG to date to make the devices quicker and more portable.
(July 2021) Navy ditches futuristic railgun, eyes hypersonic missiles:
After $500mm spent, US Navy has pulled the plug (for now) on the railgun which fires projectiles at up to
seven times the speed of sound using electricity.
Its new focus is a hypervelocity projectile that can be fired from ship's existing missile systems.
https://apnews.com/article/technology-business-a67d3200fad72488ebb37ce1b46bce5b
(July 2021) Many technologies can help GNSS, but few can replace it - GPS World:
Blog Editor's Note: "Yeah, verily" to the author's point that anyone who talks about replacing GNSS is blowing smoke (and probably selling something).
Unfortunately when we talk about ADDITIONAL or ALTERNATE sources of
PNT, folks often wrongly think "replacement," or "duplication," or "redundant."
(Of course, you say redundant to engineers and their eyes light up in adoration.
You say the same thing to budgeteers and their cost cutting knives
come out.)
When we talk about the need for sources in addition to GPS/GNSS we aren't saying that
PNT baby is ugly and should be done away with. We are saying it
is precious and deserving of our utmost care and protection.
That's why, in the words of Texas Transportation Institute Director Greg
Winfree, we need to "get the bullseye off GPS." One of thousands of reasons why
America needs to have additional, widely adopted, PNT sources.
Our adversaries have long realized that relying entirely on space for such essential services is tantamount to putting your neck on the chopping block
and waiting for the axe to fall. It is time we do as well.
Whoa, whoa, whoa, isn't that a bit over dramatic? Where do you get off with such statements? - "Neck on the chopping block," "waiting for the axe to fall"
- indeed!
OK, sure. We could probably use more discussion about repairing the condo building's foundation before we actually do something.
Let's talk more about pipeline and other cyber-security, ensuring electricity in Texas during the winter, fixing the levees in New Orleans, hardening
cockpit doors against hijackers, the health impacts of tobacco, installing seatbelts in cars. - What's the worst that could happen?
---------------------------------------------------
BTW- Welcome back to Matteo Luccio, the new Editor-in-Chief at GPS
World. Matteo began his career in the industry in 2000 as Managing Editor at GPS
World before moving on to other opportunities. He has recently returned to this new role!
Many technologies can help GNSS, but few can replace it:
Matteo Luccio
Alternative. Complementary. Backup. Co-primary. These are
some of the terms used to refer to sources of positioning, navigation and timing (PNT) data
other than GNSS satellites.
The four current GNSS constellations — supplemented by two regional ones and by public and private augmentation systems — have firmly established
themselves as the primary source of PNT data by virtue of their accuracy, reliability, global coverage and ubiquitous use. Yet, this widespread
dependency on them — especially on GPS — coupled with their well-known vulnerabilities to jamming, spoofing, other RF interference, multipath,
solar flares and space debris (see page 10) — make the development of alternative sources of PNT data
imperative. In fact, the U.S. Congress has
repeatedly mandated it.
Typically, when talking about alternative PNT, we are referring to sources of PNT data that either were not originally developed for navigation purposes
— such as television broadcast towers used as “beacons of opportunity” — or
that use a higher broadcast power or a different frequency band than
GNSS. They include legacy systems and new versions of legacy systems, such as
eLoran.
READ MORE: https://www-gpsworld-com.cdn.ampproject.org/c/s/www.gpsworld.com/many-technologies-can-help-gnss-but-few-can-replace-it/amp/
(July 2021) U.S. Navy Ship Spoofed to Crimea:
Last week a UK Royal Navy destroyer and Dutch Royal Navy ship safely
moored in Odessa, Ukraine, were spoofed to appear to be at locations off-shore of a
Russian naval base on Crimea.
This week, it was a US Navy ship moored in the same port that was spoofed.
These are interesting cases in several ways.
First, how was it done?
No other vessels seem to have been impacted. So this is much different from the wide-area spoofing the Russians have long conducted in the area.
It could have been highly targeted GPS spoofing that only impacted the three
ships. But the three ships were in port alongside a pier. Did they
even have their GPS and AIS activated?
It could be that GPS spoofing had nothing to do with it and just AIS signals were imitated and detected by satellites.
It's possible that the AIS equipment aboard the three ships was programmed by the ships' crews to transmit the false
information.
Second, who did it?
The Russians are clearly capable of doing this. They have regularly spoofed large numbers of vessels in the Black Sea over the last five years.
This was a bit different as only one or two vessels were impacted, but it is not that big
of an additional challenge
The NATO (UK, Dutch, US) crews could have done it. They certainly had access to the equipment and the ability to do it.
Could have been a third party? Perhaps a bit more of a challenge than for the other folks, but not a particularly
a heavy lift for a reasonably competent
RF hacker.
Third, why was it done?
If it was the Russians, likely yet another demonstration of their impressive electronic warfare capability and to show dominance over the West
If it was the NATO ship crews, perhaps it was a way of nettling the Russians without the trouble of having to actually sail
by. Or trying to confuse
them with a feint. The UK ship, HMS Defender, actually sailed something close to the spoofed route several days later and was harassed by Russian
forces.
- Will be interesting to see if the US Navy ship does the same.
If it was a third party, perhaps it was just to cause confusion, hate, and discontent. In the
1997 James Bond film "Tomorrow Never Dies" the super-villian
spoofs a Royal Navy ship into Chinese waters to provoke an armed conflict. See clip on our YouTube channel here.
Interesting to see life imitating art 24 years later!
(July 2021) Alternate navigation using satellite signals of opportunity -
Roke:
Blog Editor's Note: We remember about 10 years ago when smart GNSS folks said this likely possible but not practical and wouldn't result in anything
worth using. A number also said spoofing was theoretically possible but would never be a practical
threat. It is interesting to see how many things have
changed since then.
GPS is a good example of how, with enough time and effort, possible can often become practical.
Some trace GPS back to a couple guys at JHU APL
listening to the doppler on Sputnik in 1957 and calculating its trajectory and positions. Getting location information from a satellite was possible,
but not practical. It took 36 years (1993) until the first GPS constellation was operational.
(Comment by Tom Kerr: NAVSAT/Transit was done much
earlier for U.S. submarines.)
This idea is also currently being investigated by others including Army Futures Command and the
UT Radionav Lab. Perhaps its time has come.
Another thing to remember is that a system doesn't have to perform as well as GPS to be
useful. GPS often provides way more than users need.
GPS might give you 27 inches accuracy, for example, but how many of us could make do with 100 feet or even 100
yards? Especially if we are
just looking for a fall back for when GPS is not available or trustworthy for whatever reason?
We also note that the UK is especially interested in this problem. At least at the political level,
much of the justification for investing
in OneWeb was to offset being excluded from Galileo after Brexit.
It will be interesting to see how well these kinds of efforts do, and how well they need to do, to be successful and adopted for use.
Alternate navigation using satellite signals of opportunity
THE CHALLENGE
We are heavily reliant on Global Navigation Satellite Systems
(GNSS) for navigation, positioning and timing services, both for critical infrastructure
and military operations as well as in normal life. However, GNSS signals are weak, making then
vulnerable to both deliberate and accidental
interference and deception (spoofing). An alternate means of navigation is required to take over when GNSS is completely denied
and to validate
it when it is not.
THE APPROACH
Stronger satellite signals at similar frequencies can be used to supplement and take over from GNSS signals, creating signals of opportunity to
support positioning and timing. They are designed to communicate with small terminals such as satellite phones or modems, so can be processed to
a similar size as a traditional GNSS receiver. Unlike terrestrial signals of opportunity like
TV transmitters or mobile basestations, satellite
signals have the advantages of providing global coverage and are not vulnerable to local power disruptions or outages. Roke was funded by the
Defence Science and Technology Laboratory (Dstl) to investigate this approach, and we constructed a prototype antenna array capable of receiving
satellite signals from a range of different sources in L and S bands. This enabled
measurement of direction, Doppler, and propagation time for
each satellite. We then conducted a number of 4x4 trials to confirm the
conclusions from the outcome.
THE OUTCOME
This research shows that that is possible to exploit the transmissions from the existing
Iridium, Globalstar, and Orbcomm constellations to achieve
navigation and timing for a moving platform. This is currently realized using an antenna array but could be achieved from a single antenna for more
space constrained platforms. Future work would seek to further improve positioning accuracy by exploiting more satellite signals and to mature the
concept to higher Technology Readiness Levels (TRL), in collaboration with
government, military users, and industrial partners.
READ MORE & Watch Video: https://roke.co.uk/innovations/alternate-navigation-using-satellite-signals-of-opportunity
(July 2021) GPS at risk: Those signals are more vulnerable than you realize:
That has people worried about how to protect them and what we're doing for backup.
https://www.cnet.com/news/gps-at-risk-those-signals-are-more-vulnerable-than-you-realize/
(This link has accompanying images when it was streamed on 10 July 2021)
The Cessna Citation Excel was approaching the Sun Valley, Idaho, airport when something seemed off about its flight path. Like a lot of planes,
it was tuned to GPS for guidance. Usually, that's a good thing. On this day in August
2018, however, a problem arose. The GPS signals near the
airport were unreliable, and smoke in the area made for poor visibility. The midsize business jet was off-course and flying too low in the
mountainous terrain.
The likely cause for the wonky GPS readings? Military activity that caused jamming of the
signals, according to an account from NASA's Aviation
Safety Reporting System, which collates information provided by pilots, air traffic controllers and other aviation professionals. Fortunately,
radar on the ground provided a more accurate reading, and controllers got the plane to its destination safely.
Robert Rodriguez/CNET
It wasn't an isolated event, according to reporting by IEEE Spectrum and
others.
GPS is all too susceptible to jamming and its trickster cousin, spoofing. The signals used by aircraft, ships, farm tractors and your smartphone
originate from satellites 12,000 miles (19,300 kilometers) out in space. By the time they reach Earth,
they're vanishingly weak and easily overwhelmed.
A satellite launched in June to the GPS constellation represents a tiny step in making the service more secure. But satellites themselves face dangers.
All those threats have lots of people worried. Just about everything, you see, relies on GPS.
The highly precise signals from the Global Positioning System have worked their way into nearly every fabric of modern
life, from recording bank
transactions to synchronizing electrical grids to helping you find the nearest
Starbucks. Businesses and individuals can use the system's PNT --
positioning, navigation and timing -- capabilities for next to nothing. In the US,
GPS has about $1 billion a day in economic impact, according to
the National Institute of Standards and Technology. It's also vital to the operations of the US
military.
There's so much riding on GPS that a 2018 federal law sought to address one of the biggest underlying issues: the absence of a dedicated
backup.
Any substantive damage or disruption to the system would be bad news.
"My hope is we can get ahead of the bang and at least get ... some resilience put in the systems [that depend on GPS] before the bad thing
happens,"
says Dana Goward, president of the Resilient Navigation and Timing
Foundation, a Washington, DC-based nonprofit.
A backup would have a lot to prove.
"It's actually hard to create this giant, one-size-fits-all replacement for
GPS," says Richard Mason, a senior engineer at Rand Corp. and lead author
of a report on national PNT capability commissioned by the Department of Homeland Security in 2019 and released to the public in May of this year. The
report is skeptical about how much government intervention is needed, despite GPS'
vulnerabilities.
On the plus side, says Mason, "there are lots of little partial backups."
For instance: Your phone could lose GPS, Mason says, and it would still give you some sense of where you are based on
cellular signals (what's known as
assisted GPS), though not as precisely. Aircraft have alternative navigation
systems. Financial firms can get timing services from other sources.
So what's the big deal then? It's that we're addicted to GPS on a grand scale.
Those signals from space have become "the de facto national reference," the National Security Telecommunications Advisory Committee said in a report to
President Joe Biden in May. "Such wide adoption means their vulnerabilities pose a near-existential threat."
The group recommended the government develop a strategy for a "National Timing Architecture" and appropriating sufficient funds to create it.
The threats facing GPS:
There's precedent for the US government to fund something like GPS because it built GPS in the first place, primarily as a military technology, starting
in the 1970s. By the 1990s, satellite navigation was starting to become a noticeable part of civilian life.
Right now, Washington spends about $1.8 billion a year to keep GPS up and running. The US Space Force manages the satellites and the ground stations that
track them. (It took over the responsibility from the Air Force after it was spun out into a separate branch
in December 2019.) The Transportation Department is the lead civilian agency for PNT efforts.
The GPS constellation consists of 31 satellites located in medium Earth orbit. Those satellites carry atomic clocks, and onboard radios send precise
timing signals from them to receivers on the ground, including the GPS chip in your phone. GPS signals reach more than 4 billion military and civilian
users worldwide, according to the Space Force.
Those timing signals get translated into location data when a receiver syncs up signals from multiple satellites. The way the satellites are spread out
around the globe, you should always be within sight of at least four.
GPS was the first of what's known as a global navigation satellite system, or
GNSS. But it isn't the only one: China's Beidou, Russia's Glonass and the
EU's Galileo all serve similar purposes. In 2018, the FCC authorized Galileo signals for reception in the US, which means they could serve as a GPS
backup, at least to a degree. But GPS itself is the only system under US control.
All satellites are vulnerable to threats out in orbit over which we have little control. For example,
space debris could damage individual satellites,
or severe solar storms might short circuit the operations of hundreds or
more.
They're also vulnerable to anti-satellite weapons and cyber intrusions by potential adversaries who know how much our economy and our military depend
on satellites. The more satellites you knock out or confuse, the worse off we are.
Gen. John Raymond, head of the US Space Force, told the House Appropriations Committee defense subcommittee in May that we need to be worried.
"Both China and Russia are developing capabilities to deny our access to space," Raymond said. "There's an active threat in the domain."
But the more immediate dangers are more down to Earth: jamming (broadcasting a signal that's stronger than the weak one coming from space)
and spoofing
(broadcasting a signal that looks like GPS and feeding false information). It's cheap and easy to get away with.
The Russians have jammed or spoofed GPS
signals in Scandinavia, Ukraine and Syria. North Korea has targeted them in South Korea. And then there are those flight disruptions in the US,
which may,
ironically, have resulted from the US military's efforts to figure out how to deal with that problem.
"The threat that we're most concerned about with GPS is jamming," Raymond said.
The law seeking a GPS backup
A few years back, the National Timing Resilience and Security Act directed the transportation secretary to establish a land-based timing system that could
serve as a backup for GPS within two years. That deadline came and went in late 2020, but in January of this year the Transportation Department reported
to Congress on the "roadmap to implementation" it's been following toward that goal.
A companion DOT report detailed a variety of technologies that could provide "complementary service in the event of GPS disruptions." Some commercially
available technologies, it said, could go part way toward mimicking GPS' timing
services. But the agency said none would be able to serve as a universal
backup for the positioning and navigation capabilities.
Of the 11 technologies evaluated by the Transportation Department, one hit the mark in all the use cases:
a metropolitan beacon system made by Sunnyvale,
California-based NextNav. The beacons -- transmitters that send out the radio signals -- are set up on land, rather than in space, and are clustered in
urban areas (hence "metropolitan").
For NextNav, the real-world application is its up-and-coming TerraPoint
service, which gives a glimpse of how GPS-like capabilities are possible from
something that isn't GPS.
TerraPoint beacons, set up on cell towers and building rooftops, are about the size of a dorm room refrigerator, sporting an omnidirectional antenna and
a 110-volt power supply, and they're spaced about eight to 10 kilometers apart (versus that 12,000-mile range for GPS). That makes for a much more robust
signal. CEO Ganesh Pattabiraman estimates they're "about 100,000 times stronger than GPS."
The commercial service that NextNav is working toward would be independent of
GPS but function just like it, providing full position, navigation and
timing data, according to Pattabiraman. Each of its transmitters has an atomic clock and sends a precise, low-frequency timing signal to receivers
equipped with chips from companies such as Broadcom and GCT Semiconductor that support GPS, Galileo, Glonass and other GNSS. The service is designed
to operate with mass market devices like mobile phones, cars and drones as the network gets built out.
"It looks just like another GPS signal," Pattabiraman said. To the receiver, "it's just another constellation, except it happens to be land-based."
TerraPoint is deployed at scale only in the San Francisco Bay Area, where eVTOL companies like Joby Aviation are doing tests with it for urban
navigation, takeoff and landing operations. It has a more limited presence in a number of other areas, too.
NASA, for instance, has deployed a
TerraPoint network at Langley, Virginia, for urban drone operations. NextNav expects that an acquisition announced in June, and done with a public
offering in mind, will give it funding to expand.
Key to getting any GPS alternative into widespread use is to make it as easy to use as, well,
GPS. Alternatives like the now defunct Loran radio
navigation system required separate and bulky receivers, and the US government put an end to it a decade ago. Some companies are working on services
using what's known as enhanced Loran, aka eLoran, but it has yet to become more than a niche application in the US.
"The good thing about NextNav, and things like NextNav," said Rand's Mason, "is that [eventually] it would just be in every
smartphone, and so you're
using it whether you know it or not."
That isn't to say a GPS backup has to be earthbound. Companies like Satelles, which also participated in the Transportation Department demonstrations,
use the Iridium constellation of low Earth orbit satellites at an altitude of just 480 miles (780 km). It's already providing timing and location
services, deployed as a backup for GPS for customers including financial networks and energy utilities.
A startup called Xona Space Systems is designing its own low-orbit PNT
system. In May, the Defense Advanced Research Projects Agency, or DARPA, awarded
Northrop Grumman a contract to demonstrate how low-orbit satellites would perform providing PNT
signals. Researchers are looking into whether SpaceX's
Starlink satellites, built to beam broadband from orbit to Earth, could be pressed into service as a PNT
resource.
Some of those options are still just on paper. But even those that are in operation don't have the scale of the long-established
GPS.
Meanwhile, GPS itself is getting a boost. The GPS satellite that went up in June is the fifth in a new series known as
GPS III, which is designed to be up
to three times more accurate and have up to eight times the anti-jamming
capability. For the military specifically, it's helping enable the encrypted
M-Code signal that's tough on jamming and spoofing.
Eight times a weak signal, however, still isn't a signal that's much of a match for powerful jammers and spoofers operating nearby.
The role of government:
What makes GPS so attractive for so many applications is that it already exists. It's essentially universal. It's cheap and easy to use. That also makes
it hard to muster enthusiasm for spending time and money to come up with something that does what it does, as widely as it does.
Plus, those partial backups add up to … something.
The big question is how much the US government needs or wants to lean into building a sizable backup for
GPS.
Rand recommends restraint, though it acknowledges there are some potential federal initiatives that could be
cost-effective, including a timing-only
backup or law enforcement efforts focused on GPS jamming.
"There's not a compelling case for government to do a lot more than it's doing or [to do] a big new backup system," Mason said. "There's also the
question of, 'Is anybody going to use it?'"
That isn't good enough for Goward, of the Resilient Navigation and Timing Foundation. He sees China as having thoroughly outpaced the US in
establishing a sophisticated, comprehensive approach to PNT that includes three types of satellites at different altitudes, plus
eLoran and PNT
capabilities in the telecom system for independence from space.
He wants lawmakers to take action soon.
One thing Congress will have to consider: the budget proposed in late May for fiscal 2022, which starts in October, includes a line calling for the
repeal of the National Timing Resilience and Security Act -- a tacit acknowledgement
that we aren't likely to see that GPS backup mandated by the law
anytime soon. (It also includes $10 million for research into backup and complementary systems.)
Goward estimates the US might be able to spend just $50 million to $75 million a year for a timing system that everybody in the country could access.
He calls it "budget dust" compared with what we're already spending on GPS.
"The next step," he says, "is for Congress to decide what it wants to do."
In the meantime, the jamming goes on, and pilots like those in that Cessna outside Sun Valley will need to cast a wary eye on what their
GPS device is
telling them.
GPS rules everything. A new satellite launch keeps a big upgrade rolling:
It's a lot more than just driving directions. Managed by the US Space Force,
GPS factors into a huge amount of the high-tech world we live in.
On June 17, about 10 minutes after noon local time, a SpaceX Falcon 9 rocket rose into the heavens from Cape Canaveral, Florida, carrying a boxy,
5,000-pound, antenna-studded GPS satellite toward its destination 12,500 miles away, up in what's known as
medium Earth orbit. From that distant
vantage point, it'll soon beam signals that'll help you find your way to your cousin's new house out in the suburbs or a vacation destination two
states away.
If you stop at an ATM along the way to grab some cash, those signals will also help the bank know your withdrawal happened after your direct deposit
paycheck refreshed your finances. They'll be a factor, too, in whether your cellphone call to your cousin, or the rental agent, goes through without
garbling or fading.
Those signals may well be coming from a GPS III satellite, the newest members of a constellation of satellites that have become a constant and
intimate presence in our daily lives. With GPS III, we're getting not just new boxes in the sky, but a series of upgrades that'll help make the
system better for all of us here on Earth. And we'll need it.
The Global Positioning System has become vital to nearly all sectors of the country's critical infrastructure, with much of its work happening
behind the scenes, and likely to a much greater extent than you realize. GPS tells us where we are and helps us get where we're going, but a core
aspect of the technology is when — the timing of, well, more or less a zillion things.
It plays a critical role in financial transactions and
stock trades, forecasting the weather, monitoring earthquakes and keeping the power grid humming.
"It's so much more than just driving directions," says Tonya Ladwig, acting vice president of space navigation systems at Lockheed Martin, which
built that satellite.
According to a June 2019 study commissioned by the National Institute of Standards and Technology,
GPS has about $1 billion a day in economic impact
in the US. Its reach is, simply, mind-blowing.
"Gauging the overall value of GPS is nearly impossible," writes Greg Milner in Pinpoint, a 2016 book about how the space-based system came to be and
the effect it's having on the world. "It has become difficult to untangle the worth of
GPS from the worth of everything."
That's a lot to put on the shoulders of not much more than a couple dozen satellites and what turns out to be a wisp of signal by the time it reaches
your phone or an airplane coming in for a safe landing. Which is why experts and lawmakers have long fretted over
GPS' susceptibility to jamming and
spoofing and the possibility that this invaluable resource could become a single point of massive failure.
I think most people don't realize how much they depend on GPS day in and day out. It would be a bad day if we didn't have
GPS.
Maj. Gen. DeAnna Burt
GPS is the premier service among just a handful of global navigation satellite systems, or
GNSS, which include the European Union's Galileo, Russia's
Glonass and China's BeiDou. It's in the midst of a long-running modernization intended to deliver better signals to folks on the ground and to make the
satellites more robust in space. That's good news not just for Uber drivers, pilots, bankers, geologists, farmers doing precision agriculture, and users
of drones and self-driving cars, but also for the sector that got the whole GPS ball rolling in the first place:
the US military.
And the military isn't just a heavy-duty GPS user. It also runs the service, for all of us around the world.
How GPS works: Atomic clocks in space:
What makes GPS an always-on resource -- every bit as much a reliable utility as the electricity and water in your house -- is the coverage the satellites
provide.
There are 31 satellites in the GPS constellation, and 24 are considered the minimum for the core constellation to work as it's supposed to. Those two
dozen are spread out in six orbital planes, so you should always be within view of at least four at any given moment. The remaining seven are essentially
spares, to be rotated in as necessary. Though they're continuously beaming signals down to Earth that you'll pick up in your phone, fitness tracker or
boating sat-nav device, they don't know where you are. They just broadcast, like a radio station in space.
"The GPS satellites are actually just highly precise atomic clocks, hooked to a radio transmitting a time signal," says Dana
Goward, president of the
Resilient Navigation and Timing Foundation, a Washington, DC-based nonprofit.
On the ground, your GPS receiver -- which is what your iPhone or Galaxy phone is, thanks to a
GPS chip -- picks up the signals from four or more satellites.
By measuring slight differences in the signals' time of arrival, all the way down to nanoseconds, it can calculate where you are and whether you're in motion.
"[Location] is a byproduct of how the system works," says Scott Burgett, director of
GNSS and software engineering at Garmin, which makes devices including
fitness trackers and smartwatches. "All the satellites transmit signals, and they're synchronized pretty accurately, but in order to actually get your
position information, you have to solve for time."
The timing data gets translated into highly precise three-dimensional location information -- latitude, longitude and altitude -- as well as speed and
direction. That's where Google Maps, Apple Maps and other geographic information systems come into play. It's how we get to the part where you have a
street address and you say, "I'll put that in my GPS," and Waze lets you know to take Exit 27, go 3.5 miles and turn left into the parking lot of the
beer and burger joint you've heard good things about.
Or it just gets used as a time stamp, pure and simple. Think financial transactions, for instance.
"The timing aspect of this is probably more widely used than the where-are-you aspect," Goward says.
How Space Force fits in:
The US Space Force operates and maintains the GPS constellation. Each satellite -- picture a
PODS storage container, metallic rather than white, with
solar arrays sticking out like a pair of wings -- makes two transits around the planet every day.
Even as precisely programmed as those orbits are, the satellites still need their flight paths tended to around the clock.
"Those GPS vehicles are only as accurate as the data we provide them," says 1st Lt. Andrew Johnson, a crew commander in the 2nd Space Operations
Squadron, or 2 SOPS. "We get where the satellite thinks it is, we know where the satellite is, and we'll basically bake that into a nice little
message, we'll send it up to the vehicle, and the vehicle goes, 'OK I'm actually here,' and that change in information
fine tunes the signal."
Two members of the 2nd Space Operations Squadron designate the first GPS III satellite as healthy and active for users on Jan. 13, 2020. To make room for
it, 2 SOPS pushed a GPS IIA satellite to a higher, less congested, "disposal orbit." Designed for 7.5 years of service, the older satellite had been
operational for 26 years.
Johnson and 2 SOPS (pronounced "two sops") keep tabs on the
GPS satellites from Schriever Air Force Base, located just east of Colorado Springs, Colorado.
There are also 16 tracking stations scattered around the globe.
It's no accident that the US Space Force, spun off a year and a half ago from the Air Force Space Command and carrying on its
GPS mission, is wrangling a
service that's vital to devices used by millions of civilians and businesses worldwide. The origins of
GPS stretch back to secret work by the Department
of Defense in the 1970s, in a quest for precision targeting. As Milner recounts it,
GPS chief architect Brad Parkinson summed up that goal in the phrase
"Drop five bombs in the same hole."
In 1983, after a Korean Air Lines passenger jet strayed into Soviet airspace and got shot down, killing 269 people, President Ronald Reagan declassified
GPS to give civilian aircraft access to the navigation signals. Almost a decade later, GPS famously earned its stripes as a military resource during
Operation Desert Storm, when it helped guide US and allied forces across desert expanses to a swift victory over Iraq during the Gulf War.
Space has become a junkyard, and it's getting worse
How SpaceX Starlink broadband will envelop Earth and transform the sky
Orbits explained: It's hard to get into space -- but great once you're there
Space Force still has military users top of mind as it carries out its GPS mission.
"For us, it's to deliver sustained, reliable GPS capabilities to America's
warfighters," says Maj. Gen. DeAnna Burt, director of operations and
communications at Space Force headquarters in Peterson Air Force Base, Colorado. Space Force also works closely with civilian and commercial partners
to keep things running smoothly, she tells me. "We're always looking to improve not only our military capabilities but our civilian capabilities as well."
Though the funding to keep things running goes through the Pentagon -- the Space Force GPS program has a 2021 fiscal year budget of nearly $1.8 billion --
there's civilian oversight as well. The Defense Department and the Transportation Department co-chair the US government's National Executive Committee for
Space-Based Positioning, Navigation and Timing, which coordinates GPS-related matters across federal agencies and includes representatives from Boeing,
Garmin, Google, Ohio State and Stanford.
Note the keywords in that committee name: positioning, navigation and timing, or
PNT. Where you are, where you're going, and when the signals hit a receiver.
It's a term that's inescapable when you're talking with folks who live and breathe GPS.
What we're getting with GPS III:
Like any technology of a certain vintage -- the Air Force Space Command declared full operational capability for GPS in April 1995 -- the system needs to
be regularly updated, and what that means right now is GPS III.
Here's what GPS III promises: The signals will be up to three times more accurate, and they'll have up to eight times the anti-jamming capability, though
you and I probably won't see dramatic changes anytime soon. The satellites are projected to have a 15-year lifespan, double that of those from the early
part of the previous generation, though the older ones have tended to stay in business longer than expected. A modular design means it's easier to make
timely changes on the assembly line or to send software uploads to the satellites on orbit.
There's also a new civilian frequency, called L1C. Besides helping with signal strength, it's
compatible with Galileo, the EU's counterpart to GPS.
In November 2018, the FCC authorized Galileo signals to be received in the US, which made it that much more likely you'll have multiple satellites in view
-- in the double figures even, when technically you only need four to get a good, accurate
location.
The addition of the L1C signal with GPS III will likely make matters even better.
"If you have more satellites," says Garmin's Burgett, "you can have more direct line-of-sight signals available to you, and you can get a better
fix."
The military, meanwhile, is getting, among other things, the encrypted M Code that's key to the enhanced anti-jamming and anti-spoofing
capabilities, as
well as spot beam capability for focused signals in combat areas. The satellite that launched June 17 is the 24th satellite equipped with M
Code, which
will make the feature fully operational. "What that M Code does is ... it'll allow you to receive the encrypted signal much faster," says Burt, the Space
Force general.
A little bit down the road, the addition of a laser retro-reflector array will allow the positioning of satellites to be refined via ground-based laser.
The first of the GPS III generation of satellites, all built by Lockheed Martin
at its Littleton, Colorado, facility, lifted off in late 2018 and became
operational in January 2020. The second, third and fourth also became operational
as that year rolled along. The latest satellite, dubbed SV05,
was the first GPS III satellite to be launched in 2021; it became operational last week, and
the Space Force expects it to become available to all
global users in September.
Lockheed Martin has a contract to deliver a total of 10 GPS III satellites, at a reported average cost of $529 million apiece, but the company says the
last two of them will come in at around $200 million each. When that's done, it'll move ahead with a batch called
GPS III F, an additional 22 satellites
to continue replacing older models, through the coming decade.
"It takes a long time to replenish the GPS constellation," Burgett says. "It takes years."
GPS' weak spots:
It might seem like GPS is pretty much always there when you need it, but it's more vulnerable than you may realize. If you live in a city with tall
buildings, you've probably fumed waiting for an Uber driver to get to where you're standing -- it could be that buildings are blocking the satellite
signals in what's known as the urban canyon effect.
That's a line-of-sight issue, and it can often be resolved by moving, if you can, to a spot with a better view of the heavens. The US government says
that GPS-enabled smartphones are typically accurate to within a 16-foot (5-meter) radius under the open sky.
Then there's interference -- other, stronger signals making too much radio "noise" nearby. Experts routinely refer to the
GPS signals as weak by the
time they get from outer space to phones and other gear on Earth, and that relative lack of strength can be a serious problem.
"Because it's such a weak signal, it's very, very easy to block, to jam," Goward says. "Virtually any noise within that frequency is going to keep you
from hearing the GPS signal."
Space Force's Burt likens it to a nearby sound system at full blast: "If you were at the dinner table and there was a 500-watt stereo playing at full
volume in the kitchen, would you be able to hear the conversation going on around you? You might pick up pieces, parts of it, but not pick up all of it."
The US military has to worry about hostile forces jamming or spoofing GPS signals to hide troop movements or to keep friendly forces from getting where
they're supposed to go, or weapons from hitting their targets.
Outside of war zones, some countries use GPS interference to mask the whereabouts of
VIPs, while criminals use it to pull off shipping heists. The
nonprofit Skytruth, which uses satellite images and data to track polluters and
poachers, in 2019 reported on GPS manipulation at oil terminals in
China likely intended to hide activities that run afoul of export controls.
The Pentagon and other government agencies, meanwhile, are aghast at the Federal Communications Commission's approval in April 2020 of a controversial
plan by a company called Ligado to create a nationwide 5G network. The frequencies
Ligado would be using are very close to those employed for GPS.
Ligado says it's sorted out any interference issues, but Defense Department CIO Dana Deasy said in a Senate hearing in May 2020 that
"there are too many unknowns and the risks are too great."
The vulnerabilities of the satellite signals are something the GPS community has been thinking about for a long time, along with the need for some sort
of backup. The idea is to provide a ground-based service -- such as what's known as
eLoran -- that might not be as good but that would suffice when
somebody's jamming or spoofing or if the satellites aren't available.
There have been a number of false starts down that road over the years. A new push came at the end of 2018 with the
National Timing Resilience and
Security Act, which directed the Secretary of Transportation to establish a terrestrial timing system that could serve as a backup for GPS within
two years. We're past that mark now, with nothing much to show for it. The Transportation Department did issue a report to Congress in January of
this year showing how various "complementary PNT and GPS backup technologies" performed in demonstrations.
A more limited proposal came in February 2020 when President Donald Trump signed an executive order on
PNT, which at least got the NIST in October to
draft guidance on developing a timing system free of GPS.
In the years ahead, there will be more Space Force rocket launches carrying the latest
GPS III satellites from Lockheed Martin. Modernization of the
constellation will continue apace, new applications will appear, and as much as we're hooked on GPS services now, we're likely to only get more dependent.
Satellite timing is everywhere on Earth and in everything.
"I think most people don't realize how much they depend on GPS day in and day out,"
Space Force's Burt says. "It would be a bad day if we didn't have GPS."
Originally published Nov. 23, 2020.
(July 2021) Ensuring Continuous PNT Services:
All sectors of the economy are adversely impacted by GPS/GNSS
vulnerability. However, the impact is different in each sector. RF interference could have
tremendous impact across different sectors, including offshore oil and gas, agriculture, automotive, construction, mining, or even within the consumer market. How do
we protect GNSS against vulnerabilities and minimize the risks?
Read this opinion piece by Michael Ritter, President, Hexagon AB here: https://buff.ly/3hVQhZo
https://www.gwprime.geospatialworld.net/opinion/ensuring-continuous-pnt-services/
(July 2021) Spoofing GPS in Indonesia to Make Things Work Better - Vice:
https://www.vice.com/en/article/7kvpng/delivery-drivers-are-using-grey-market-apps-to-make-their-jobs-suck-less
Blog Editor's Note: "Adversarial Interoperability (AKA Competitive Compatibility/comcom), the practice of modifying an existing technology against
the wishes (or without permission) of its maker."
We were certainly familiar with the practice, but learned the name of the phenomenon while researching this piece.
In this instance, corporate overlords require that the driver closest to the call gets to respond. But that just causes massive traffic james of
drivers wanting to be near popular pickup spots. Something that is not in anyone's best interest.
People jam and spoof GPS for lots of reasons. Most not so good. Sometimes to not let the rules keep them from doing the right thing.
Tech by Vice
Delivery Drivers Are Using Grey Market Apps to Make Their Jobs Suck Less
In Indonesia, unofficial apps let delivery drivers filter orders and spoof their
GPS location to beat the algorithms at their own game.
RQ
By Rida Qadri
The McDonald’s on Jalan Salemba Raya, Jakarta’s crowded main thoroughfare, is a magnet for food delivery orders. On any given day, a dozen or
so app-based delivery drivers—locally called ojol—wait in the parking lot. Inch by inch, they try to move as close as they can to the center
of the lot, desperate to have the matching algorithms recognize their proximity and assign them an order.
But even more drivers are there virtually, using GPS-spoofing apps to position themselves right in the center of the McDonald's lot while they
physically wait under nearby shelters. Using these unofficial apps, known as tuyul, drivers can set their GPS pins at the optimal location they
would like orders from, without having to physically drive there.
In Jakarta, these kinds of unauthorized apps are a common tool-of-the-trade among app drivers working for Gojek, a $10 billion delivery and
transport "super app" that is the Indonesian equivalent of Postmates, Apple Pay, Venmo, and Uber. Though Indonesia is by far its biggest market,
Gojek operates in more than 200 cities in Indonesia, Singapore, Vietnam, and Thailand.
READ MORE: https://www.cnbc.com/2021/01/27/gojek-wants-to-expand-further-outside-indonesia-this-year-co-ceo-says.html
(July 2021) Does Anybody Really Know What Time It Is? - Does Anybody Really Care... About Time?:
Yes, there are folks who know what time it is.
And, yes, there are lots of folks who care!
In fact, just about everyone cares, though most most folks don't realize it.
Precise time underpins virtually every technology from navigation systems, networks, cell phones, and digital broadcast, to financial transactions
and control systems for electrical grids.
So, whether they know it or not, pretty much everyone cares - a lot!
The folks who really know what time it is are NIST and USNO (even though they usually disagree by a handful of nanoseconds. Wonder why this isn't
pico or femtoseconds?)
Most of us use USNO time because USNO feeds GPS. And, regardless of whether you are on a computer or cell phone, if you trace the time source back
far enough, you are likely to end up at a GPS signal.
This makes GPS, in the words of one DHS official, a "single point of failure."
We should have other ways besides GPS to ensure folks can access precise time. As part of its tech infrastructure, for example, China has instituted
multiple ways, both wireless and wired, for its citizens and applications to access precise time.
Our white paper "A Resilient National Timing Architecture" discusses how the US we can use policy and technology to provide multiple, resilient paths
to precise time for all its citizens for about $50M to $75M a year.
The telecommunications industry agrees the US needs this. In May, a group of telecom CEOs and senior execs told President Biden he should work with
industry and fund a national timing architecture. A telecom industry standards group told Congress the same thing a day later.
And Congress agrees the country needs this. The National Timing Resilience and Security Act of 2018 was signed by President Trump and requires a
terrestrial timing system to work with and backup GPS be established by December of last year. Sadly, the last administration failed to request or
identify funding and nothing has been done yet.
This year the new administration has requested funding to study the issue (again). Let's hope Congress is more action oriented and provides funding
for a solution.
Because we really do need to know what time it is. And we really do care... about time.
https://www.slideshare.net/MarcoLisi/its-all-about-time?trk=v-feed
(July 2021) US Space Force issues ICD revisions for GPS - GPS World:
The U.S. Space Force Space and Missile Systems Center (SMC) has issued official, signed
Interface Specification
(IS) and Interface Control Document
(ICD) revisions for GPS. Read more at the link below.
https://www.gpsworld.com/us-space-force-issues-icd-revisions-for-gps/
(July 2021) Trio of HawkEye 360 formation-flying microsatellites launched for RF geolocation - GPS World:
HawkEye 360 Inc. successfully launched its Cluster 3 radio frequency geolocation microsatellites built by
Space Flight Laboratory (SFL). They join
in orbit the HawkEye 360 Cluster 2 and Cluster 1 Pathfinder satellites. Read more at the link below. (Artist’s rendering: Hawkeye 360)
https://www.gpsworld.com/trio-of-hawkeye-360-formation-flying-microsatellites-launched-for-rf-geolocation/
HawkEye 360 Inc. announced the successful launch of its Cluster 3 radio frequency geolocation microsatellites built by
Space Flight Laboratory (SFL).
Carried aboard the June 30 SpaceX Transporter 2 mission, the Cluster 3 formation-flying microsatellites quickly established communication with the
company’s satellite operations center. They join in orbit the HawkEye 360 Cluster 2 and
Cluster 1 Pathfinder satellites.
The HawkEye 360 Constellation detects and geolocates RF signals for maritime situational awareness, emergency response, national security and spectrum
analysis applications. Cluster 3 significantly expands HawkEye 360’s capacity, and is part of its second generation of advanced
RF-sensing satellites.
“With the addition of our second-gen satellites, we’ll offer more frequent, timely and actionable data and insights to our government, commercial and
humanitarian partners,” said CEO John Serafini.
“The increased revisit frequency and capacity Cluster 3 brings to our constellation are essential to detecting, characterizing, and understanding the
continuously changing RF activity important to our clients,” said Alex Fox, Executive Vice President for Sales and Marketing.
Seven more clusters are fully funded and scheduled for launch in 2021 and 2022 to achieve collection revisits as frequent as every 20
minutes, Fox said.
“Each cluster will offer new innovations to address a rapidly growing set of requirements needed by our defense, security and commerce clients. We plan
on expanding the constellation past the initial 10 clusters to achieve near-persistent monitoring of global RF
activity, which will drive even more
value and ensure our continued dominance in the industry.”
HawkEye 360 delivers a layer of intelligence to help understand human activity on Earth. The constellation detects, characterizes and precisely
geolocates these RF signals from a broad range of emitters, including VHF marine
radios, UHF push-to-talk radios, maritime and land-based radar
systems, L-band satellite devices and emergency beacons.
By processing and analyzing these RF data, the company delivers actionable insights for national, tactical and homeland security operations,
maritime domain awareness, environmental protection and new applications in the commercial sector, the company said.
The HawkEye 360 launch brings to 20 the total number of SFL satellites placed into orbit in less than a
year. The Cluster 3 satellites were built
on SFL’s 30-kg Defiant microsatellite bus.
HawkEye 360 selected SFL due to the importance of formation flying by multiple satellites for successful RF geolocation. SFL is the acknowledged leader
in developing and implementing high-performance attitude control systems that make it possible for relatively low-cost nanosatellites and microsatellites
to fly in stable formations while in orbit.
The previous HawkEye 360 satellite clusters built by SFL were the Pathfinder launched in 2018 and Cluster 2 in January. Each Cluster is comprised of
three satellites.
Other launches of SFL-built satellites in the past year include missions developed for the
Norwegian Space Agency (NOSA) in Norway, the Dubai-based
Mohammed Bin Rashid Space Centre (MBRSC) in the United Arab Emirates,
GHGSat Inc. of Canada, Space-SI of Slovenia, and a Canada-based
tele-
communications company.
(July 2021) GNSS as an Instrument of National Power - GLONASS Case Study:
Blog Editor's Note: This article is about GLONASS but could be easily about GPS, Bei Dou, or even
Galileo. Certainly they are instruments of soft power
(economic, political, etc,), And they have the potential for espionage and other national applications.
Several particularly interesting bits in this piece.
First, the question from the Czech government as to whether the GLONASS ground station the Russians asked to place in their country would be passive or
emitting. Long time, still no answer from the Russians. Hence no Czech ground
station. Probably a good idea.
Second, the idea that GLONASS ground stations and satellites could likely also serve as intelligence gathering assets, or more.
Third, that Russia may want wide adoption of GLONASS so as to insulate the system from deliberate jamming, spoofing, cyberattack, and so on:
"There’s also a safety-in-numbers approach to Russia’s sales pitch. The more countries dependent on
GLONASS, the less likelihood there is for any one
of them to try to hack it. “It is very tricky to want to mess with the U.S. GPS system,” Porras told Newlines, “in large part because you don’t know
how widespread the implications can be.” Russia, he said, wants in on that deterrent capability."
Interesting idea. It seems to us, though, that, if GLONASS were to be widely adopted, it would become a more attractive target for most, rather than
less. Perhaps some participating nation-states might be less likely to hack it, but then they probably would not have been big threats to begin with.
Adversary nations, terrorists, and rouge hackers, on the other hand, would be more interested in hacking it if the impacts were going to be more widely
felt.
Perhaps Russia is not quite so concerned because it has a terrestrial Chayka/Loran system that operates
in parallel with GLONASS/GNSS. Very adept at
electronic warfare themselves, perhaps they have already ensured their critical infrastructure, systems, and applications use
both GNSS and Chayka.
Finally, the comment at the end of the article that Russia "...is focused on advancing its own national interest at the expense of other nations.”
Without being too cynical, we expect that, upon closer examination, EVERY nation is always seeking to advance its own national
interest. Those nations
with a short time horizon, perhaps those driven by an individual who only cares about what can be done during their time in
power, tend to take
advantage of other nations. Those with a longer time horizon see the value of respecting others and cultivating good long relationships. Some are
better than others, but no nation has been able to do this consistently.
GLONASS, Moscow’s answer to GPS, is set to launch an upgraded satellite network later this year,
which it hopes to sell to the U.S. and Europe. Buyer
beware!
Holger Roonemaa, Holger Roonemaa is an investigative journalist based in Tallinn, Estonia
Michael Weiss, Michael Weiss is a senior editor at Newlines
July 12, 2021
Russia is preparing to introduce a new generation of its GLONASS satellite navigation system, with expanded global infrastructure.
Several Western
intelligence agencies say the program is also being used to conduct high-level espionage.
A joint investigation by Newlines, Delfi.ee in Estonia, and Respekt magazine in the Czech Republic reveals that
GLONASS contains two new mechanisms
for conducting espionage, including on nuclear weapons systems.
READ MORE: https://newlinesmag.com/reportage/western-intelligence-fears-new-russian-sat-nav-espionage-capabilities/
(July 2021) Parrot's new ANAFI Ai UAV drone is 4G connected - GPS World:
Drone-maker Parrot has released a new drone for professionals. The ANAFI Ai UAV uses
4G as its main data link between the drone and the operator,
so that users will no longer experience transmission limitations. Read more at the link below.
https://www.gpsworld.com/parrots-new-anafi-ai-uav-drone-is-4g-connected/
Drone-maker Parrot has released a new drone for professionals. The ANAFI Ai UAV uses
4G as its main data link between the drone and the operator,
so that users will no longer experience transmission limitations.
The 4G also enables precise control at any distance. For beyond-visual-line-of-sight
(BVLOS) flights, it stays connected even behind obstacles.
For the first time, ANAFI Ai embeds a secure element in the drone and in its
Skycontroller 4. The 4G link between the drone and the user’s phone
is encrypted. The secure element protects both the integrity of the software and the privacy of data transferred.
Parrot’s piloting application is open source. Parrot offers developers a software
development kit (SDK) to create custom code for the drone to
execute during flight. The SDK gives access to all flight sensors, including obstacle-avoidance sensors, occupancy grid and internet access.
ANAFI Ai’s obstacle-avoidance system detects obstacles in all directions, using stereo cameras to sense objects and automatically avoid
them.
ANAFI Ai incorporates a 48MP main camera and a powerfully stabilized
4K 60-fps/HDR 10 camera to capture finely detailed aerial images and smooth
video footage.
ANAFI Ai will be available in the second half of 2021 through Parrot Drone Enterprise Partners and Enterprise Drone Reseller Network.
(July 2021) Nanosatellites Could Play Pivotal Role in Defense Against Enemy Missiles:
"These satellites will test key technologies that mitigate risk for systems, such as the
Hypersonic and Ballistic Tracking Space Sensor," Walt Chai,
MDA director for space sensors, said. "The CNCE Block 1 mission will demonstrate the viability of advanced communications technologies using reduced
size, weight and power in support of missile defense communications architectures."
(July 2021) US Air Force plane navigates by tiny changes in Earth's magnetic field:
It's exciting to see magnetic navigation being utilized and tested more and more. While offering more challenges to overcome initially,
MagNav is far
more difficult to jam than traditional GPS systems and therefore offers a more robust and trustworthy navigation system with the increased data coming
from test flights such as these.
"A simple compass needle aligns with the strong magnetic field produced by Earth’s liquid-iron core, but a more sensitive magnetometer can also pick
up fainter magnetic fields embedded in rocks that make up Earth’s crust. These fields have a pattern as complex and distinctive as topography. By
measuring the strength and direction of the crustal field and how it changes during a flight, you can work out where you are in the magnetic landscape."
https://www.newscientist.com/article/2283597-us-air-force-plane-navigates-by-tiny-changes-in-earths-magnetic-field/#ixzz701fa5ZC6
(July 2021) China’s Beidou system makes great strides in adoption: white paper - Global Times:
Blog Editor's Note: We thought we would offer this article as a follow-on to yesterday's post about
GNSS as an instrument of national power. China is
particularly good at using Bei Dou for soft power.
Also note how they have used Bei Dou as to stimulate economic growth domestically, and to ensure their sovereign independence from non-Chinese system.
We are not sure folks in the US have really learned the lesson of how GPS stimulated so much growth and generated so much economic benefit.
If they had, perhaps the US would be more eager to, like China, build upon that success and develop other national
PNT, both terrestrial and at LEO.
Caveat: Global Times is an arm of China's state media. As such, everything should be taken with a grain of salt. Nevertheless, the article provides
good insight into China's government's thinking.
China’s Beidou system makes great strides in adoption: white paper:
By Global Times Published: May 18, 2021 08:28 PM
China's self-developed BeiDou Navigation Satellite System (BDS) has been widely adopted in a wide range of areas, including transport, public security,
agriculture and other activities related to people's daily life, according to an industry report on Tuesday.
Underscoring the widespread adoption, the number of devices such as smartphones that have BDS navigation functions has reached 1 billion at the end of
2020, showed the white paper released by the GNSS and LBS Association of
China.
Sales of chips and modules that are compatible with the BDS exceeded 150 million sets as of
2020, with quarterly shipments of more than over 10 million
sets. Meanwhile, total shipments of Beidou-powered high-precision chipsets, modules and boards surpassed 1 million last
year, with main application
scenarios including connected cars, drones and agricultural machinery.
The BDS also played a major role in China's fight against the COVID-19 outbreak, surveying and drawing plans based on BeiDou's high-precision technology
greatly reduced the time needed to build healthcare facilities in Central China's Hubei Province and Northwest China's Shaanxi Province, among other regions.
Globally, BDS has been providing services to more than 100 million users, with solutions like precision agriculture, vehicle and ship monitoring, and smart
ports having been successfully applied in ASEAN, South Asia, Eastern Europe and other regions, according to the white paper.
International mainstream chip manufacturers also widely support the BDS, while most smartphone series of Chinese brands including Huawei, Vivo, OPPO and
Xiaomi are Beidou-compatible, it said.
Behind the impressive numbers lay China's constant vitality in technological innovation. In 2020,
28-nanometer SoC chips, which enable mobile devices to
receive signals from Beidou-3, were widely used in the Internet of Things and the consumer electronics sectors.
A more advanced 22-nm chip that supports dual-frequency positioning and will further increase the accuracy of the system has entered mass
production.
The white paper pointed out that in order to realize self-reliance in key sectors and deal with challenges brought about by the industry's development,
more work should be done to actively support the standardized development of the BDS and promote comprehensive, large-scale application of the technology.
In China, the satellite navigation and location services industry is becoming mature, with all links on the industry chain expanding in 2020.
READ MORE: https://www.globaltimes.cn/page/202105/1223806.shtml
(July 2021) You’ve got space mail!:
This week, find out how we’re teaming up with the European Space Agency to address global climate change.
Read this story & more: https://conta.cc/2UVl3K4
(July 2021) GPSPatron seeks to protect critical infrastructure - GPS World:
GPSPatron is offering products and services to protect equipment, particularly
GNSS-dependent critical infrastructure. Its GP-Probe TGE2 is designed
to protect time servers against threats including spoofing, jamming, ionospheric scintillation and system errors. Read more at the link below.
https://www.gpsworld.com/gpspatron-seeks-to-protect-critical-infrastructure/
(July 2021) The growing problem of jamming and spoofing of GPS satellite navigation signals just keeps getting worse - M&AE:
Blog Editor's Note: Our initial response to this article was "Duh!" Aside from stating the obvious, it is a short piece that, initially, doesn't
seem to add much to the community discussion.
But it does point out that the problem "keeps getting worse." And why wouldn't it?
Equipment to interfere with GPS/GNSS continues to become less expensive, easier to use, and more capable.
And, as we regularly show in this space, people continue to find new reasons to interfere with the signals. Everything from great power competition
between navys to delivery drivers subverting the dumb decisions of their cluesless
bosses.
Also, there is little movement to make GPS/GNSS signals more difficult to
disrupt. Sure, the US military has M code and Galileo is instituting
PRS
service, but these are marginal improvements at best, are costly, and are not available to 99% of users who aren't in government.
Sad that China is so far ahead of the West on this. They have established
PNT capability in LEO, MEO, and GEO, expanded eLoran to
cover the whole
country, are using 5G telecom for PNT, and are aggressively working on inexpensive clocks and
IMUs.
While not as advanced as China, Russia, South Korea, Iran, Saudi Arabia and others
are still way ahead of the West.
What's it gonna take for the US and Europe to wake up?
Oh, by the way, there is one more bit this very short article adds to the discussion - the subhead
"There's precedent for the US government to fund
something like GPS because it built GPS in the first place..."
An interesting point for those in government who want to shirk responsibility for protecting the public.
John Keller, chief editor
Military & Aerospace Electronics
July 20th, 2021
The growing problem of jamming and spoofing of GPS satellite navigation signals just keeps getting worse:
There's precedent for the US government to fund something like GPS because it built
GPS in the first place, primarily as a military technology.
WASHINGTON – The Cessna Citation Excel business jet was approaching the Sun Valley, Idaho, airport when something seemed off about its flight path.
Like a lot of planes, it was tuned to GPS for guidance. Usually, that's a good thing. On this day in August 2018, however, a problem arose. The
GPS
signals near the airport were unreliable, and smoke in the area made for poor visibility. The midsize business jet was off-course and flying too low
in the mountainous terrain. CNET reports. Continue reading original article
The Military & Aerospace Electronics take:
20 July 2021 -- The likely cause for the wonky GPS readings? Military activity that caused jamming of the signals, according to an account from
NASA's
Aviation Safety Reporting System, which collates information provided by
pilots, air traffic controllers and other aviation professionals. Fortunately,
radar on the ground provided a more accurate reading, and controllers got the plane to its destination safely.
It wasn't an isolated event. GPS is all too susceptible to jamming and its trickster cousin, spoofing.
READ MORE: https://www.militaryaerospace.com/rf-analog/article/14207023/gps-signals-jamming
(July 2021) UrsaNav trials eLoran as vital GNSS backup using ADVA’s grandmaster clock solution - Business Wire:
Blog Editor's Note: Another example of timing and navigation interests joining forces.
Full disclosure - UrsaNav and Oscilloquartz, an ADVA brand, are
both corporate members of the RNT Foundation.
UrsaNav trials eLoran as vital GNSS backup using ADVA’s grandmaster clock solution
July 27, 2021 03:00 AM Eastern Daylight Time
NORTH BILLERICA, Mass.--(BUSINESS WIRE)--ADVA (FSE: ADV) today announced that
UrsaNav and ADVA have conducted an enhanced
long-range navigation (eLoran) field trial using UrsaNav’s eLoran receiver and
ADVA’s Oscilloquartz grandmaster clock technology.
The successful demo shows that eLoran offers a robust and reliable backup for
GPS and other GNSS and could be used to provide an
assured position, navigation, and timing (PNT) service. The trial follows US federal executive order 13905 aimed at strengthening
national resilience through PNT services, including protecting critical infrastructure such as electrical power grid and communication
networks from rising cyber threats. By harnessing ADVA’s flexible OSA 5420 Series, designed with
assured PNT (aPNT) technology, UrsaNav
has shown that eLoran can provide a new layer of protection and significantly boost timing resilience and
security.
READ MORE: https://www.businesswire.com/news/home/20210727005101/en/UrsaNav-trials-eLoran-as-vital-GNSS-backup-using-ADVA%E2%80%99s-grandmaster-clock-solution
(August 2021) Combating Foreign Disinformation on Social Media Study Overview and Conclusions:
by Raphael S. Cohen, Nathan Beauchamp-Mustafaga, Joe Cheravitch, Alyssa Demus, Scott W. Harold, Jeffrey W. Hornung, Jenny Jun, Michael Schwille, Elina Treyger, Nathan Vest
Related Topics:
Cyber Warfare,
Information Operations,
The Internet,
Psychological Warfare,
Social Media Analysis
How are state adversaries using disinformation on social media to advance their interests? What does the Joint Force—and the U.S. Air Force (USAF)
in particular—need to be prepared to do in response? Drawing on a host of different primary and secondary sources and more than 150 original
interviews from across the U.S. government, the joint force, industry, civil society, and subject-matter experts from nine countries around the
world, researchers examined how China, Russia, and North Korea have used
disinformation on social media and what the United States and its allies
and partners are doing in response. The authors found that disinformation campaigns on social media may be more nuanced than they are commonly
portrayed. Still, much of the response to disinformation remains ad hoc and
uncoordinated. Disinformation campaigns on social media will likely
increase over the coming decade, but it remains unclear who has the competitive edge in this
race; disinformation techniques and countermeasures
are evolving at the same time. This overview of a multi-volume series presents recommendations to better prepare for this new age of communications
warfare.
Key Findings
Disinformation campaigns on social media might be more nuanced than commonly portrayed
Russia and Iran have used this tactic abroad more than China and North Korea have.
State-led disinformation campaigns on social media are a relatively recent phenomenon.
The campaigns can intimidate, divide, and discredit, but there is limited evidence that they can change strongly held beliefs.
Smaller, locally popular social media platforms could be at higher risk of disinformation than larger, mainstream ones.
Disinformation campaigns on social media have clearly notched operational successes, but their strategic impact is less certain.
Disinformation campaigns on social media will likely increase over the coming decade.
Much of the response to disinformation remains ad hoc and uncoordinated
The U.S. government's lead for countering disinformation, the Department of State's Global Engagement Center, lacks the necessary
political and institutional clout to direct a coordinated effort.
The joint force's efforts to man, train, and equip forces for counter-disinformation remain ad hoc and service-dependent.
Allies and partners have tried other countermeasures, mostly with ambiguous effects.
Industry—particularly after the 2016 election interference—has made an active effort to counter disinformation, but companies'
responses are shaped by their business models.
Civil society groups play an important, often overlooked role.
Although disinformation campaigns on social media will likely increase over the coming decade, it remains unclear who has the
competitive edge in this race because disinformation techniques and countermeasures are evolving at the same time
Recommendations
The USAF, in general, and Air Force Special Operations Command, in particular, should expand their information operations capabilities
and responsibilities.
The joint force should know the information environment and look beyond U.S. platforms. It should also train for disinformation, focus
on key demographics, minimize widespread bans on smart phone and social media use, increase transparency, enforce message discipline,
and conduct a Department of Defense–wide review of the information operations force.
The U.S. government should publish a counter-disinformation strategy, leverage civil society groups and industry without outsourcing th
e counter-disinformation fight, avoid bans on social networks, balance counter-disinformation efforts with a commitment to freedom of
speech, and carefully weigh risks while focusing offensive influence efforts on truthful information.
(August 2021) Upgrades to NASA’s Space Communications Infrastructure Pave the Way to Higher Data Rates:
The ability to transmit and receive data is crucial in space exploration. Spacecraft need robust networking capabilities to send data –
including large files like photos and videos - captured by onboard instruments to Earth as well as simultaneously receiving commands
from control centers. NASA has made significant strides to improve the agency’s space communications capabilities while simultaneously
maintaining ongoing operations and service to a large number of missions.
https://www.nasa.gov/feature/goddard/2021/upgrades-to-nasa-s-space-communications-infrastructure-pave-the-way-to-higher-data-rates
(August 2021) What happens to British ships when satellites don't work? - BBC News:
Blog Editor's Note: This article has a number of interesting observations even though it conflates and confuses satnav and satcomms.
The comments by the former head of the British Navy (First Sea Lord), who was also the nation's first minister for cybersecurity, are
particularly worth noting. Some examples:
"I thought I'd ask the government, I thought they'd have processes, but it became very clear from their answers that they don't understand
what the problem is."
"If you don't have a fallback for a system, you can bet your bottom dollar that someone will exploit that,"
"GPS can very easily be messed up. We know the Russians are practicing
this."
Also interesting that the government spokesperson said mariners should be proficient in celestial navigation as a backup. Celestial nav i
s OK if you are at sea, not in danger of hitting anything, and want to have a rough idea of where you are amongst the great waters. Not so
much otherwise. There are other backup methods for close in. But if we really can't trust electronic nav, that ripples through the entire
staffing, training, equippage and cost equation and has major impacts on the safety and effectiveness of both naval and merchant operations.
The government rep just shrugging the problem off and saying "celestial" like it is a magic bullet just reinforces the First Sea Lord's comment
that they don't understand the problem.
We do note in all fairness that, as mentioned in Parliament, the UK government has a national PNT Strategy under
development. No information is
available, though, on when it will be published.
Also, our experience in the U.S. government is that strategies are often published as a way to give the impression of action without having to
actually do anything. We have been informed by some who have reason to know that this is not the case in the
UK, or at least won't be the case
for the PNT strategy.
Let's hope.
What happens to British ships when satellites don't work?:
By Richard Morris
Political reporter, BBC News
28 July 2021
The Royal Navy and Britain's merchant fleet, along with most others around the world, rely on satellites for navigation - but what happens if
they don't work?
It's a question that troubles the former First Sea Lord, Lord West of Spithead, who has spent months trying to find out if the UK has a back-up plan.
"My concern is that those people who are not friends with us are looking at ways to knock out satellite communications," he says.
"I thought I'd ask the government, I thought they'd have processes, but it became very clear from their answers that they don't understand what
the problem is.
"There's no proper system for achieving communication if satellites collapse."
The Labour peer, who was the UK's first cyber-security minister under Prime Minister Gordon Brown, is convinced the government needs to act to
protect the British fleet.
"If you don't have a fallback for a system, you can bet your bottom dollar that someone will exploit that," he says.
"The best fallback is probably old VHF [radio] systems. GPS can very easily be messed up. We know the Russians are
practicing this."
READ MORE: https://www.bbc.com/news/uk-politics-57440787
(August 2021) 17 Statistical Hypothesis Tests in Python (Cheat Sheet) - Machine Learning Mastery:
https://machinelearningmastery.com/statistical-hypothesis-tests-in-python-cheat-sheet/
Last Updated on November 28, 2019
Quick-reference guide to the 17 statistical hypothesis tests that you need in
applied machine learning, with sample code in Python.
Although there are hundreds of statistical hypothesis tests that you could use, there is only a small subset that you may need to use in a machine
learning project.
(August 2021) 1National PNT Infrastructure; Getting the U.S. on the Path to Resilience - ION Newsletter:
Blog Editor's Note: An excellent summary of where America has been with PNT resilience and policy and where it needs to go.
Interesting to note that the false rationale "GPS is expensive so we need to economize and have fewer other PNT sources" seems to have persisted
from the 1980's until today. It doesn't help that the way the Department of Defense describes GPS III makes it sound like it will solve all the
nation's problems.
As the good book says, "The sins of the father shall be visited upon the children to the third and fourth generation." Not a threat so much as a
description of the way society works.
We really enjoy the news, commentary, interviews, and navigation history in the quarterly ION Newsletters. If you are not already an ION member,
we heartily recommend it. Visit https://www.ion.org/
Getting the U.S. on the Path to Resilience
Doug Taggart, President, Overlook Systems Technologies, Inc.
There is a dichotomy between our national space-based positioning, navigation and
timing (PNT) policies and the decades-old recognition that
overreliance on the Global Positioning System (GPS) as the single source for
PNT leaves U.S. critical infrastructure vulnerable.
The May 2021 Colonial Pipeline computer hack serves as an all too recent example of how vulnerable Americans are to single-source supply chains.
The hack, attributed to a group known as DarkSide, shut down 5,500 miles of pipeline, interrupting the flow of gasoline across the United States’
Southeast and MidAtlantic regions.
The ramifications of an intentional disruption of GPS have been theorized about and analyzed ad nauseum. Even if only one specific sector of our
critical infrastructure was the primary target of a space-based PNT
interruption, there would most certainly be collateral damage beyond the
intended target.
We must find a way to get out of this unending refusal to address the reality of overreliance. Though national
spacebased PNT policy, dating back
to the Bush era, has highlighted the need for a backup to GPS, nothing has been done to date.
The 1984 Federal Radionavigation Plan’s (FRP) Executive Summary contained a passage that clearly conveyed the challenge of
meeting the needs of
all PNT users. “The goal [of the FRP] is to select a suitable mix of these common civil/military systems which can meet diverse user requirements
for accuracy, reliability, coverage, operational utility, and cost; provide adequate capability for future growth; and minimize duplication of
services. The process of selecting a system mix is a complex task, since user requirements vary widely and change with time.”
READ MORE: https://rntfnd.org/wp-content/uploads/ION-Summer21-Doug-Taggart.pdf
(August 2021) The Biden Administration and Civil PNT – So Far, So Good. Sorta. - ION Newsletter:
Blog Editor's Note: The author is President of the RNT Foundation.
This article was written a month or so ago when the newsletter was in preparation.
Since then the infrastructure bill has been formulated in the Senate
without any mention, so far, of needed essential infrastructure in the form of a complement and backup for GPS.
Also in the news since that time have been a lot of reports about Chinese and Russian anti-satellite
technology, and what it means for GPS. And these
reports are coming from government sources like General Raymond, the Space Force
Commander.
Stay tuned...
The Biden Administration and Civil PNT – So Far, So Good. Sorta.
By Dana Goward, President of the Resilient Navigation & Timing Foundation
The Biden administration has proposed $17 million in funding for resilient civil positioning, navigation and timing (PNT) efforts at the
Department of
Transportation (DOT) for fiscal year 2022. While this might
not be much compared to DOT’s overall PNT responsibilities, it is a marked increase over the
estimated $5 million being expended this year and the $2 million spent last fiscal
year.
Who Decides?
While presidents have long acknowledged the importance of civil use of the Global
Positioning System (GPS) and PNT, their administrations, regardless of
party, have struggled to match that with funding. This is likely because, while the
DOT is the lead for civil PNT issues, GPS is seen as a Department of
Defense (DOD) responsibility. Requests to fund GPS and PNT needs through
DOT are difficult to explain to harried bureaucrats and congressional
staff.
Also, for the most part, civil PNT issues have been relatively low profile, not rising to the attention of the chief executive.
Aside from President
Reagan making GPS available for civil use and President Clinton doing away with selective
availability, civil PNT issues generally have been the
province of career civil servants.
This has given career staff closest to the White House an outsized role. Until recently,
they had not shown much visible interest in civil PNT issues.
Often, they have been actively hostile.
As one example, despite President Bush’s 2004 mandate for a backup capability for GPS, staff at the Office of Management and Budget
(OMB) were able to
block the announced solution in the first days of the Obama administration. This
despite four years of government wide research, negotiation, and broad
agreement on the way forward.
Again, in 2015, after the Obama administration wrote Congress saying it would build a terrestrial backup for
GPS, OMB staff made sure nothing ever
happened.
This seems to also have been true in the Trump administration. In 2018 President Trump signed legislation that included the
National Timing Resilience
and Security Act (NTRSA). The Act required at least one terrestrial timing backup for
GPS be established by December 2020. Yet no action was taken to
comply. Having failed to meet, or even work toward, the Act’s deadline, in February 2020 the administration instead issued Executive Order 13905 focusing
on encouraging civil GPS users to protect themselves.
In its last days, the administration did publish a new national space-based PNT policy that addressed a number of civil PNT
issues. It called for, among
other things, additional research, and interference monitoring and detection. Also, for the government to “…identify and implement, as appropriate,
alternative sources of PNT for critical infrastructure, key resources, and mission-essential functions.”
Senior Leaders Engaging
The long-standing status of civil PNT as a third- or fourth-tier issue
may be changing with the Biden administration.
Political appointees seem very much aware of PNT’s importance, the impact of the
Federal Communications Commission’s (FCC) decision in favor of Ligado
Networks, extensive jamming and spoofing around the world, and the fact
that—unlike China, Russian, Iran and others—the United States has no widely
implemented fallbacks or alternatives to space-based PNT. They are also aware that the
NTRSA remains unexecuted and there is political peril in America
not being prepared for yet another nationwide problem. These have all been reflected in reported comments by
Department of Transportation Secretary Pete
Buttigieg, DOT Deputy Secretary Polly Trottenberg, and other senior members of the administration.
Bringing even more awareness of PNT issues to the Biden administration is Caitlin Durkovich, senior director for resilience and response at the National
Security Council. She previously served in the Obama administration as assistant secretary for infrastructure protection at the Department of Homeland
Security. In that role she became very much aware of the importance of PNT, once describing GPS as a “single point of failure.”
Increased Funding Proposed
This increased awareness and appreciation at senior levels already has influenced the budget process — a clear indicator, as then-Senator Biden said, of
what people really care about.
The $17 million requested for resilient PNT issues in the administration’s
proposal for fiscal year 2022 is grouped in three areas. While it is questionable
whether this amount will be sufficient for the listed efforts, it is at least a start.
A sum of $3.5 million is requested for “GNSS Performance Monitoring and Interference Detection
Capability.” This one is really two related projects.
The first is civil GPS signal monitoring. Convincing folks within the administration and/or Congress
of the need for this has been a multiyear challenge
for DOT. It is good to see the Biden administration agreeing with the need right off the
bat.
The second is for establishing an interference monitoring and detection capability that could also geolocate disruption
sources. This has been discussed
as a “should do” in policy documents since 2004. The Federal Communications
Commission’s decision on Ligado Networks may have been the final impetus for
action as it is mentioned as part of the budget justification.
Another $3.5 million is requested for “Executive Order 13905 Implementation and GPS Signal
Authentication.” This is another two-parter. The first is
vulnerability assessments and studies. The second will look at validating and authenticating civil GPS signals.
The lion’s share of the request, $10 million, is for “GPS Backup/Complementary PNT Technologies
Research.” This is to execute the recommendations from
the DOT GPS Backup Technology Demonstration. It will fund efforts to develop
alternate PNT safety-critical standards for transportation, performance
monitoring capabilities, and a vulnerability and performance testing
framework.
A Strange Twist/ Insult to Congress?
One facet of the budget request that has baffled members of Congress and their staffs, as well as outside observers, is a proposal in the budget
submission to repeal the NTRSA.
One congressional staff member who, like all the others who shared their perspectives for this story, spoke on background due to ongoing budget
negotiations, said, “We are stunned. This is the exact opposite of what we have been hearing from senior leaders in
DOT and expecting in the budget.”
Another was shocked when no one from the administration consulted with concerned members of Congress before sending the proposal forward. “I can think
of very few instances when an administration has surprised and embarrassed members like this. Not even a phone call or email to explain or give us a
heads-up. It’s a real insult.”
Speculation as to how this happened and what it means abounds.
“Numerous senior administration officials seem to agree with doing something to
execute the Timing Act,” said one retired official. “The lack of
coordination with Congress tells me that this likely was slipped in by someone at OMB thinking it would be under the political
radar.”
As to motivation, some say that it is a continuation of decades-old opposition within
OMB to doing anything to protect civil users. The philosophy
being the government should not be in the civil PNT business. Others say that it is more of a process concern than opposition to establishing a timing
capability. “OMB has long opposed PPPs [public private partnerships],” said a Capitol Hill staffer familiar with the issue. “They see
NTRSA as facilitating
a PPP, and they hate that.”
Still Talking
With a pandemic to battle, an economy to restore, the climate to rescue, and a volatile international situation to work on, it is likely that senior folks
in the Biden administration have not had much time in the last six months to think a lot about civil
PNT. And realistically, compared to so many other
things, civil PNT is going along OK, for now.
And while the landscape and players may be confusing, Americans concerned about civil
PNT issues might be encouraged, nonetheless. If the old Hollywood
maxim, “It doesn’t matter what they say, as long as they are talking about you,” holds true, things are looking up. Despite everything,
the level of
conversation in Washington about civil PNT has never been higher.
RNTF will be hosting GAO Report sessions at ION’s JNC and ION GNSS+.
On May 10, 2021, the Government Accountability Office (GAO) released its report “Defense Navigation Capabilities:
DOD is Developing Positioning, Navigation,
and Timing Technologies to Complement GPS.” Among the report’s recommendations were that the
Department of Defense consider using resilient technologies
as the cornerstone of its PNT efforts going forward, instead of its current plan to build its plans around
GPS.
The full report is available for download at: https://www.gao.gov/assets/gao21-320sp.pdf
The Resilient Navigation and Timing Foundation hosted a webinar, facilitated by
ION, on the report that can be viewed for free at:
https://www.ion.org/publications/webinar-GAOreport.cfm
The Resilient Navigation and Timing Foundation will be hosting informational sessions at
ION’s JNC and ION GNSS+ conferences with the report’s
authors and invite interested parties to attend.
GET PDF OF ARTICLE HERE: https://rntfnd.org/wp-content/uploads/ION-Summer21-GOWARD.pdf
(August 2021) Canada, Denmark, Finland, Iceland, Norway, Russia, Sweden, and the U.S. have long cooperated in the Arctic
region
—even when their respective interests have clashed on other matters.
But conditions in the Arctic are evolving. This new report examines:
https://www.rand.org/pubs/research_reports/RRA1007-1.html?utm_campaign=&utm_content=1628721808&utm_medium=rand_social&utm_source=linkedin
(August 2021) Infrastructure Bill Neglects GPS Threats - Forbes:
Blog Editor's Note: An excellent article by RNTF member Diana Furchtgott-Roth. Diana is a professor at GWU and previously served as Deputy Assistant Secretary
for Research and Technology at the U.S. Department of Transportation.
Diana is right on target. But we need to remember that, just because this bill does not specifically mention
DOT and a complementary and backup system for GPS,
that doesn't mean all is lost.
There are sufficient laws on the books already to justify an appropriation to DOT for a complementary and backup system for GPS. These include:
-Organic DOT responsibilities outlined in Title 10 and Title 50 provisions regarding civil GPS and PNT
-The National Timing Resilience and Security Act of 20218
-Provisions included in the current infrastructure bill regarding support for broadband (PNT is a critical enabler)
-Provisions in the current bill related to Intelligent Transportation Systems
We aren't attorneys or expert congressional staff. So if we can think of the above items there are likely more ways in which such funding can be supported
by existing law and/or through the current infrastructure bill.
Question is whether anyone in Congress thinks it is important enough, and has enough pull to do so. Let's hope.
And, of course, there is the regular appropriations process for fiscal 2022. That will still be in the works for the next month or so.
And let's all keep up the input to our legislators telling them how important this is. Maybe by forwarding Diana's excellent article!
Thanks for the great work, Diana!
Infrastructure Bill Neglects GPS Threats:
by Diana Furchtgott-Roth
Contributor on Transportation
I write on transportation and tech topics shaping tomorrow’s news.
The $1 trillion bipartisan infrastructure bill that was voted out of the Senate on August 10 has no funding for strengthening the
Global Positioning System
(GPS) to make sure that Americans can navigate without getting spoofed. The House should correct the Senate’s omission.
With $50 billion over the next decade allocated in the bill for cyber-attacks and climate change, it makes sense to designate $1 billion of this amount to the
Transportation Department to reinforce GPS.
In the last two decades, GPS has become essential foundational technology for many industries. Without accurate
GPS, daily life would become almost
unrecognizable. Imagine not having cell phone service, or the ambulance to your house being delayed while the driver consulted a road map and hunted for house
number.
Malicious interference with GPS, an invisible utility paid for by the federal government, is increasingly common.
GPS satellites could be damaged by electromagnetic
storms or hostile military action.
Today, GPS outages and gaps are real, not hypothetical. Naval ships operating in the Persian Gulf have been lured into Iranian waters and seized through
GPS
spoofing.
READ MORE: https://www.forbes.com/sites/dianafurchtgott-roth/2021/08/10/infrastructure-bill-neglects-gps-threats/?sh=55db58eb23ad
(August 2021) Startups Map Out Strategies To Augment Or Backup GPS -
SpaceNews:
Blog Editor's Note: Interesting article on some space-based services with the potential to augment or offer an alternative to GPS/ GNSS.
As we have said before, space-based systems offer things you can't get from terrestrial and need to be part of a coherent and resilient PNT architecture.
It is hard to imagine, though, how space-based alone could be sufficient.
The outlet is "SpaceNews," so it is perhaps understandable they would chose not to mention the many companies that offer terrestrial augments and
alternatives.
At the same time, establishing terrestrial systems will "take the bullseye off of space" making it a safer environment for all.
With terrestrial anti-satellite lasers, nuclear powered EW satellites lofted by Russia, and all manner of Chinese and Russian
ASAT vehicles going into
orbit, we would think space folks would be very interested in things that can de-escalate the environment. Even if those things were on the ground.
All that said, it is good to see the market ready to provide these kinds of services. A big unanswered question, though - who is going to pay, and why?
Full disclosure, Xona Space Systems is a corporate supporter of the
RNT Foundation.
Startups map out strategies to augment or backup GPS
by Debra Werner — August 4, 2021
Companies investing billions of dollars in autonomous cars, delivery drones and urban air taxis are counting on precise and reliable location data being
available when they need it.
GPS-level accuracy of 4.9 meters for a smartphone operating under clear skies won’t be good enough. Before autonomous cars can speed down highways, they
will need to know their location within around 10 centimeters with roughly one error every billion miles.
“When you start doing the math, you realize almost every car in your fleet has to have sub-10-centimeter accuracy for its entire lifetime,” said Patrick
Shannon, CEO and co-founder of TrustPoint, a startup based in Silicon Valley and Northern Virginia developing a new
global navigation satellite system
(GNSS).
READ MORE: https://spacenews.com/startup-pnt-services/
(August 2021) US Defense Department looking for GNSS disruption detection and analysis - GPS World:
US Defense Department looking for GNSS disruption detection and analysis
August 13, 2021 - By Dana Goward
Est. reading time: 1:30
The U.S. Department of Defense wants help making sense of commercially and publicly available information that could be used to
detect GNSS disruptors,
especially over large areas.
Obtaining the ability to detect and geolocate GNSS disruptions has been cited as an
unmet need in a number of U.S. national policies and plans dealing
with positioning, navigation and timing.
The recently posted solicitation calls the project “HARMONIOUS ROOK –
Situational Awareness for Intentional Disruption of Global Navigation Satellite
System (GNSS) Users.” The solicitation says:
“The Department of Defense (DoD) seeks commercial solutions leveraging machine-driven analytics and datasets derived from publicly/commercially available
information (PAI/CAI) to provide a situational awareness capability for intentional
global navigation satellite system (GNSS) disruptions. This
solicitation is particularly focused on persistent, large-area coverage of falsified GNSS emitters that result in localized spoofing phenomenology.”
Studies and analyses by non-profit organizations and commercial entities have demonstrated the ability of non-governmental organizations to do this kind
of work and produce remarkable results. In 2017, our Resilient Navigation and Timing Foundation detected and reported on
widespread GPS spoofing in the
Black Sea.
Another non-profit, C4ADS, built upon our work and produced a detailed 2019 report on
GPS spoofing in Russia and Syria. In 2019 and 2020, the
environmentally oriented non-profit SkyTruth reported on circle spoofing in
China and around the globe. In July, SkyTruth revealed warship activities
being misreported in Automatic Identification System databases.
This acquisition is being led by the Defense Innovation Unit, or
DIU. The unit was specifically created to accelerate the adoption of commercial technology
and services by the defense and national security establishments. While letting a traditional
DoD contract for a prototype can often take up to 18 months,
DIU aims to award contracts within 60 to 90 days of identifying the
problem.
To do this, DIU uses the government’s “commercial solutions opening” process, which is designed to be simple and quick.
Companies who provide analytic services and those who have unique data sets are both encouraged to apply. The deadline is August 23.
Dana A. Goward is president of the Resilient Navigation and Timing Foundation
READ IN GPS WORLD: https://www.gpsworld.com/us-defense-department-looking-for-gnss-disruption-detection-and-analysis/
(August 2021) Hackers Use Morse Code To Bypass Security:
https://www.techtimes.com/articles/264115/20210813/microsoft-discovers-new-morse-code-phishing-technique-cybersecurity-experts-confirm.htm
(August 2021) What is complementary/alternative PNT? - GPS World:
Blog Editor's Note: This is a long piece so we won't add much to it with a long commentary. Only to say that since our inception, we have endorsed the
architecture/ system of systems approach, as envisioned in the US govt's still-in-use
2008 National PNT Architecture.
Full disclosure: Spirent, Orolia, and UrsaNav are RNT Foundation corporate
supporters.
PNT powers unmanned vehicles for transportation, ag
(agriculture) and more.
August 16, 2021 - By Matteo Luccio
What is complementary / alternative positioning, navigation, and timing (PNT)? In this month’s cover story, five of our marketing partners share their
perspective on this question and explain how their products address it.
The four global navigation satellite systems (GNSS), two regional navigation satellite systems and public and private augmentation services continue to
provide exceptional levels of accuracy and reliability for positioning,
navigation and timing (PNT). Yet their well-known vulnerabilities also continue
to fuel the need for alternative/complementary sources of PNT data, especially for
new and rapidly expanding user segments such as autonomous vehicles.
What constitutes a complementary service to GNSS for PNT and what constitutes a true alternative is
partly a matter of definition and opinion. In a
January report, the U.S. Department of Transportation stated.
…suitable and mature technologies are available to owners and operators of critical infrastructure to access
complementary PNT services as a backup
to GPS. To achieve the parallel objective of resilience, as described in Executive
Order (EO) 13905, that path should involve a plurality of diverse
PNT technologies. Promoting critical infrastructure owner/operator use of those technologies that show strong performance, operational diversity,
operational readiness, and cost-effectiveness is worthwhile. Based on this demonstration, those technologies are
LF and UHF terrestrial and L-band
satellite broadcasts for PNT functions with supporting fiber optic time services to transmitters/control segments. (Andrew Hansen et al.,
Complementary
PNT and GPS Backup Technologies Demonstration Report, prepared for the Office of the Assistant Secretary for Research and
Technology, Department of
Transportation, January 2021, p. 195.
For this year’s Q&A on complementary / alternative PNT, I asked five companies in the
GNSS/PNT space to tell us how they define the issue, what solutions
they prioritize, what markets they target, and which of their products specifically address the need to make PNT more
resilient.
The participants are:
-Roger Hart, Director of Engineering, Spirent Federal Systems
-David Sohn, Solution Architect, Orolia
-Matthieu Noko, Product Manager, SBG Systems
-Jacob Amacker, Product Engineer, OxTS
-Charles Schue, Founder & CEO, UrsaNav
How do you define alternative PNT?
READ MORE: https://www.gpsworld.com/pnt-powers-unmanned-vehicles-for-transportation-ag-and-more-gps-world/
(August 2021) This collision avoidance tool could cut the risk of in-orbit crashes:
https://www.nbcnews.com/science/space/collision-avoidance-tool-cut-risk-orbit-crashes-rcna1655?utm_campaign=PR%3A%20Announcements&utm_content=176279643&utm_medium=social&utm_source=linkedin&hss_channel=lcp-7939313
The technology is designed to address one of the most pressing issues facing spacecraft operators in
low-Earth orbit.(LEO).
The U.S. Department of Defense tracks more than 27,000 pieces of space junk in low-Earth
orbit. NASA:
By Denise Chow
A new collision avoidance platform that helps space companies keep tabs on their satellites and surroundings could cut the risk of crashes in
orbit that generate harmful space junk.
Slingshot Aerospace, a startup based in Austin, Texas, and El Segundo,
California, announced Thursday the launch of the communications platform
that will allow satellite operators to assess the location of spacecraft in their fleet and coordinate any maneuvers that may be necessary to dodge
objects nearby.
The technology is designed to address one of the most pressing issues facing spacecraft operators in low-Earth orbit, as the area around the planet
has become increasingly crowded with satellite systems for telecommunications,
GPS, and other functions.
The platform, called Slingshot Beacon, aims to reduce the risk of collisions in low-Earth orbit, said Melanie Stricklan, co-founder and CEO of Slingshot
Aerospace. The company's pilot program includes the United Kingdom-based communications company
OneWeb, the data and analytics firm Spire Global,
and several other operators, accounting for 53 percent of satellite constellations in low-Earth orbit, she added.
Collision avoidance will be an essential component of the growing private space industry, particularly as an estimated 115,000 satellites are expected
to be in operation in low-Earth orbit by 2030. This is in addition to more than 27,000 pieces of space junk — ranging from defunct satellites to spent
rocket parts to wayward bits of debris — that are already tracked by the U.S. Department of Defense.
Several different agencies, including NASA and the Defense
Department, track orbital debris but Slingshot Aerospace is hoping to make it easier for
companies to communicate about collision risks and avoid potentially catastrophic situations in orbit.
"We've created a new Wild West and it didn't have to be this way," Stricklan said. "We have to keep these orbits sustainable
because the entire world is
dependent on space."
Slingshot Beacon is designed to help companies resolve issues in orbit, notify other satellite operators of planned maneuvers and mitigate future risks.
Stricklan said she hopes the tool will invite greater collaboration among companies and among various nations.
"This allows us to reduce uncertainty and communicate across borders,
across companies and across silos that exist today," she said.
The mounting space junk problem was highlighted recently, after an object crashed into the International Space Station and damaged the orbiting lab’s
robotic arm. The incident, found during a routine inspection May 12, demonstrated the growing threat posed by orbital debris and the need for greater
situational awareness in orbit.
(August 2021) New FPGA's to be made in U.S. (for critical applications):
https://www.lockheedmartin.com/en-us/news/features/2021/new-technology-revolutionizes-analog-and-digital-systems.html
Intel recently announced a new technology that enables customers to significantly reduce the size, weight, power and cost of systems used in radar,
electronic defense, high-end commercial test equipment and 5G/6G communications
markets. Delivering the highest analog converter sample rates in the
industry, this transformative technology integrates FPGAs and high-performance analog-to-digital converters
(ADC) and digital-to-analog converters (DAC),
a revolutionary step toward providing a single component to improve performance, reduce power consumption and shrink the physical size of circuitry.
With this announcement, Intel extends technology scaling from digital semiconductors into
the realm of digital plus analog applications. In 5G and 6G
applications, the bandwidth attained with such high sample rates will directly correlate to high communication bandwidth
to enable transporting the
massive amount of data the world is now moving wirelessly.
MORE....https://www.lockheedmartin.com/en-us/news/features/2021/new-technology-revolutionizes-analog-and-digital-systems.html
(August 2021) NASA Tests Machine to Power the Future of Aviation Propulsion:
https://www.nasa.gov/aeroresearch/nasa-tests-machine-to-power-the-future-of-aviation-propulsion
(August 2021) It takes GRIT to protect your position:
Available on all NovAtel OEM7 products, GNSS Resilience and
Integrity Technology (GRIT) enables situational awareness and interference mitigation tools
to protect your position, navigation and timing against global navigation satellite system
(GNSS) interference.
Detailed situational awareness is the first step to building resiliency and integrity of a user’s position.
GRIT includes NovAtel’s successful Interference
Toolkit (ITK) and spoofing detection to identify when your GNSS signal is under
threat. Once a user’s environment is characterized, GRIT enables
interference mitigation through anti-jam technology and digital filters. Users can
characterize jamming signals and develop their own interference location
algorithms.
Read more here: https://lnkd.in/gUnYm2m
(August 2021) China’s Anti-Satellite Weapons Could Conquer Taiwan—Or Start a War - The National Interest:
Blog Editor's Note: Great article showing, again, how China plays the long game. Contrast their 30 and 40 year efforts with what seems to
be a two-year planning window in the U. S. based on elections to the House of Representatives. Or maybe it is a four-year window based on
presidential terms.
And don't forget that China's emotional commitment is to neutralizing the U. S. in space because of the "unforgettable humiliation."
So... space is important. It is a battleground. The U.S. has more in space than anyone else. We
DEPEND on space more than anyone else.
Raise hands, please, if you don't understand why our space assets are gigantic, high priority targets for our adversaries.
China’s Anti-Satellite Weapons Could Conquer Taiwan—Or Start a War:
Should the United States fail to intervene, the consequences would be disastrous for both Washington and its allies in East Asia, and potentially
the credibility of U.S. defense commitments around the globe.
by Brian G. Chow Brandon Kelley
On July 1, 2021—the one-hundredth birthday of the Chinese Communist Party—President Xi Jinping declared that China will “advance peaceful national
reunification” with Taiwan. It would be easy to dismiss such statements as mere political rhetoric: certainly, Taiwan would never willingly accede
to Chinese demands to rejoin the fold. But China’s rapidly advancing anti-satellite
(ASAT) capabilities could open up another avenue: deterring
United States intervention on Taiwan’s behalf in order to coerce reunification without firing a shot.
If current trends hold, then China’s Strategic Support Force will be capable by the late 2020s of holding key U.S. space assets at risk. Chinese
military doctrine, statements by senior officials, and past behavior all suggest that China may well believe threatening such assets to be an
effective means of deterring U.S. intervention. If so, then the United States would face a type of “Sophie’s Choice”: decline to intervene,
potentially leading allies to follow suit and Taiwan to succumb without a fight, thereby enabling Xi to achieve his goal of “peacefully” snuffing
out Taiwanese independence; or start a war that would, at best, be long and bloody and might well even cross the nuclear threshold.
READ MORE: https://nationalinterest.org/feature/china%E2%80%99s-anti-satellite-weapons-could-conquer-taiwan%E2%80%94or-start-war-192135
(August 2021) Microchip offers new chip-scale atomic clock for defense - GPS World:
Microchip Technology Inc. is offering the new SA65 chip-scale atomic
clock (CSAC), providing precise timing accuracy and stability in extreme environments.
https://www.gpsworld.com/microchip-offers-new-chip-scale-atomic-clock-for-defense/
(August 2021) Joint All-Domain Command and Control: Background and Issues for Congress:
https://lnkd.in/dEzJqpNb
https://crsreports.congress.gov/product/pdf/R/R46725/2
(or maybe click here)
(August 2021) U.S. military doubles down on GPS despite vulnerabilities -
SpaceNews:
Blog Editor's Note: This article is a interesting follow-on to GAO's report on
"DoD Navigation Capabilities." The article is worth reading for additional
information it brings to light.
The author also refers to a RAND report we have discussed before that found "The military’s huge dependence on
PNT data makes GPS an attractive target for
adversaries." - Yup!
One of the big findings of the GAO report was the point highlighted in the title of this article. Also disturbing was the GAO's finding that within DOD,
Alternate PNT efforts don't have senior leader support, and senior leaders are not in the mood for a large investment in a new navigation infrastructure.
Pretty clear that this issue is in the not-yet-important category for them.
Perhaps this effort could be helped along if DOD thought about purchasing
PNT services from a commercial provider. This could likely be much less expensive
and up and running much sooner than would be the case with a government major system acquisition.
Individual leaders who understand and care can make such a difference. Without the vision and passion of
Dr. Brad Parkinson and his patron Dr. Malcom
Currie, DOD's Deputy Director of Research and Engineering, GPS would never seen the light of day. None of the services wanted it. To quote the Navy "we
already know where we are!"
RNTF hosted another discussion with staff from GAO about "DOD Navigation
Capabilities." At the ION Joint Navigation Conference last night. Here is a video
of a similar on-line discussion we hosted with ION in June. If you are wondering what in the world
DOD is thinking about wrt PNT, viewing the video and
reading the report will provide a lot of answers. Though some of them are disturbing.
Bottom line (or maybe top line) - senior DOD leaders need to start caring about the
PNT infrastructure that underpins so much of their technology. Else
everything they have now and might build will increasingly be just a house of cards.
U.S. military doubles down on GPS despite vulnerabilities:
by Sandra Erwin — August 9, 2021
Space weapons meant to target U.S. satellites are a growing concern for the U.S. military. Especially worrisome are electronic jamming devices designed
to interfere with GPS signals.
That threat is “real today and concerning,” the chief of space operations of the U.S. Space Force Gen. John Raymond told the House Appropriations
Committee’s defense subcommittee during a hearing in May.
Raymond pointed at China and Russia as the primary actors pursuing technologies aimed at “robust jamming of
GPS and communications satellites.”
READ MORE: https://spacenews.com/u-s-military-doubles-down-on-gps-despite-vulnerabilities/
(August 2021) Today at The Institute of Navigation's #JNC2021 conference:
Hexagon's Autonomy & Positioning division's president and CEO Michael Ritter presents on spoofing detection in our OEM7 receivers.
Spoofing has been a well-known threat in military applications, with operations coming under threat more frequently in recent years. For appropriate and
effective mitigation to be taken, spoofing detection must be reliable and correct.
Don't miss our presentation today at 14:10 ET at #JNC in Ballroom B.
Learn more >> https://hxgn.biz/3DcEbFk
(August 2021) https://www.nationaldefensemagazine.org/articles/2021/8/26/navy-marines-gearing-up-for-space-warfare
(August 2021) GOOD QUOTES:
James Kiessling: "AN/SPY-1 or AN/SPY-6 is pretty much irrelevant to SSA. Its a rare satellite pass / orientation that provides a suitable target
to support a current calibration assessment."
John McGlynn: "High-gain, phased-array-antennas, Wiley-Coyote-ACME Signal Processing is all cool but there's only so much power that you can put into a
transmit beam from a SHIP...it eventually comes down to Joules per dwell time and you just don't have enough when
1/R4 dominates."
(August 2021) https://devblogs.microsoft.com/visualstudio/revamped-project-properties-ui/
(August 2021) U.S. Navy and Marines gearing up for space warfare: https://www.nationaldefensemagazine.org/articles/2021/8/26/navy-marines-gearing-up-for-space-warfare
(August 2021) U.S. military doubles down on GPS despite vulnerabilities -
SpaceNews:
Blog Editor's Note: This article is a interesting follow-on to GAO's report on "DoD Navigation Capabilities." The article is worth reading for additional
information it brings to light.
The author also refers to a RAND report we have discussed before that found "The military’s huge dependence on
PNT data makes GPS an attractive target for
adversaries." - Yup!
One of the big findings of the GAO report was the point highlighted in the title of this article. Also disturbing was the
GAO's finding that within DOD,
Alternate PNT efforts don't have senior leader support, and senior leaders are not in the mood for a large investment in a new navigation infrastructure.
Pretty clear that this issue is in the not-yet-important category for them.
Perhaps this effort could be helped along if DOD thought about purchasing
PNT services from a commercial provider. This could likely be much less expensive
and up and running much sooner than would be the case with a government major system acquisition.
Individual leaders who understand and care can make such a difference. Without the vision and passion of
Dr. Brad Parkinson and his patron Dr. Malcom
Currie, DOD's Deputy Director of Research and Engineering, GPS would never seen the light of day. None of the services wanted it. To quote the Navy "we
already know where we are!"
RNTF hosted another discussion with staff from GAO about "DOD Navigation
Capabilities."At the ION Joint Navigation Conference last night. Here is a video
of a similar on-line discussion we hosted with ION in June. If you are wondering what in the world
DOD is thinking about wrt PNT, viewing the video and
reading the report will provide a lot of answers. Though some of them are disturbing.
Bottom line (or maybe top line) - senior DOD leaders need to start caring about the
PNT infrastructure that underpins so much of their technology. Else
everything they have now and might build will increasingly be just a house of cards.
U.S. military doubles down on GPS despite vulnerabilities
by Sandra Erwin — August 9, 2021
Space weapons meant to target U.S. satellites are a growing concern for the U.S. military. Especially worrisome are electronic jamming devices designed
to interfere with GPS signals.
That threat is “real today and concerning,” the chief of space operations of the
U.S. Space Force Gen. John Raymond told the House Appropriations
Committee’s defense subcommittee during a hearing in May.
Raymond pointed at China and Russia as the primary actors pursuing technologies aimed at “robust jamming of
GPS and communications satellites.”
READ MORE: https://spacenews.com/u-s-military-doubles-down-on-gps-despite-vulnerabilities/
(September 2021) With SV08, 3 GPS III satellites ready for launch:
https://www.gpsworld.com/with-sv08-3-gps-iii-satellites-ready-for-launch/
(September 2021) National Academies Proposes Team to Study FCC Ligado Decision - GPS World:
National Academies Proposes Team to Study FCC Ligado Decision
September 2, 2021 - By Dana Goward
The National Academies has announced its proposed team to examine the analysis and decision-making process by the
Federal Communications Commission (FCC)
in the matter of Ligado Networks. Individuals and organizations wishing to comment on the appropriateness of any of the members of that team or on any other
aspect of this study have until September 19.
The April 2020 decision by the FCC has generated significant controversy and opposition within the public and Congress. This resulted in, among other things,
seven separate petitions for reconsideration being filed, all of which are still pending, and several provisions in the National Defense Authorization Act
for 2021. One of those provisions requires the Department of Defense to sponsor a study of the technical assumptions and analyses that went into the
FCC’s decision to allow Ligado Networks to operate.
According to the post on the National Academies website, the study will consider:
“(1) Which of the two prevailing proposed approaches to evaluating harmful interference concerns — one based on a signal-to-noise interference protection
criterion and the other based on a device-by-device measurement of the GPS position error — most effectively mitigates risks of harmful interference with
GPS services and DOD operations and activities.
(2) The potential for harmful interference from the proposed Ligado network to mobile satellite services including GPS and other commercial or
DOD services
including the potential to affect Department of Defense (DOD) operations, and activities.
(3) The feasibility, practicality, and effectiveness of the mitigation measures proposed in the
FCC order with respect to DOD devices, operations, and
activities.”
This announcement is the first significant public step for the effort, which is expected to take
approximately 12 to 18 months. Sources say that there will
likely be public and classified versions of the report. The classified version is likely to take significantly longer to compile.
The proposed study team members are:
Chair: J. Michael McQuade
Members:
Jennifer Lacroix Alvarez
Kristine M. Larson
John L. Manferdelli
Preston F. Marshall
Y. Jade Morton
Richard Reaser, Jr.
Jeffrey H. Reed
Nambirajan Seshadri
(September 2021) James Kiessling's positive endorsement:
Sound recommendations - I normally see certain political leaning 'think tanks' as stealth marketing but this OpEd is clearly about making more effective
uses of multiple billion dollar assets and gaining capabilities far sooner. My complete technical endorsement - Well done
Heritage!.
https://lnkd.in/e7wBg3NT
(September 2021) Two years since the Tesla GPS hack:
Blog Editor's Note: An interesting reminder of a hallmark event within the PNT community. We are sure it had a significant impact on the folks at
Tesla,
and probably significant but probably lesser impact at other car companies.
We would have hoped that all GNSS users would take the lesson to heart and in the last two years taken significant steps to upgrade all their receivers
and antennas to make them more resilient to spoofing. Probably didn't happen.
Toward the end of the article Roi mentions the inclusion of cybersecurity provisions in the
U.N. regulations. Great acknowledgement of the impact of
Regulus's work and the impact it has had.
Just the U.N. saying manufacturers have to demonstrate their vehicles are cybersecure, though, is a long way from making that a reality. That will have
to be interpreted and enforced by national governments - each with their own definitions of what that means and structures for requirements and enforcement.
Well done again to Regulus making an important step in this long journey.
Full disclosure - Regulus is a corporate member of the RNT Foundation.
Two years since the Tesla GPS hack
August 30, 2021 - By Roi Mit
In June 2019, Regulus Cyber’s experts successfully spoofed the GPS-based navigation system of a
Tesla Model 3 vehicle. This experiment provided an
important warning for all companies using GNSS location and timing: these technologies, on which they depend, are highly vulnerable to spoofing attacks.
In the two years since the experiment, companies and governments have continued to research the potential harm that can be caused by spoofing attacks and
are learning more about how to defend themselves from them.
The Tesla experiment was groundbreaking because it was the first time that a level 2.5 autonomous vehicle was exposed
to a sophisticated GPS spoofing
attack and its behavior recorded.
We chose Tesla’s Model 3 because it had the most sophisticated advanced
driver assistance system (ADAS) at the time, called Navigate on Autopilot
(abbreviated NOA or Autopilot), which uses GPS to make several driving decisions. However, this experiment exposed several cybersecurity issues
potentially affecting all vehicles relying on GPS as part of their sensor fusion for autonomous decision making.
READ MORE: https://www.gpsworld.com/two-years-since-the-tesla-gps-hack/?utm_source=Defense+PNT+%2B+Geointelligence&utm_medium=Newsletter&utm_campaign=NCMCD210902002&oly_enc_id=9675F1206356D9T
(September 2021) House Armed Services Committee Interested in New, Non-GPS PNT Constellation:
The House version of the National Defense Authorization Act for 2022, which begins on the first of October, requires the Secretary of the Air Force to
provide a briefing to the Armed Services Committee about establishment of a new PNT constellation.
Specifically mentioned is the Air Force's Navigation Technology Satellite
3 (NTS-3) program. Cited in the language are the fact that is features a
"...steerable, high-power phased array antenna coupled with a digital signal generator that can be reprogrammed on orbit, enabling operators to quickly
deploy newly developed, advanced signals as they encounter electronic threats."
Also noted is that "NTS-3 will be working on PNT enhancements such as experimental antennas, flexible and secure signals, increased automation, and use
of commercial assets."
The briefing is also to include "... a detailed funding, development, procurement, and launch plan.." and talk about how satellites can be rapidly deployed
to meet emerging electronic warfare threats.
We find the mention of commercial assets and rapid deployment to be particularly interesting. Unfortunately, the briefing will undoubtedly be classified.
But we would love to be a fly on the wall.
LINK TO NDAA PROVISION: https://armedservices.house.gov/_cache/files/6/8/6851607b-a0bf-4f59-8073-69400fd673fc/EF79C94AAFA1C0E2D673B2B64EDE0830.bills-117hr4350ih-strsubcommitteemarkup.pdf#page=26
“Investment in a 21st-century Intelligent & Autonomous Infrastructure is among the highest priorities for stimulating economic expansion, national security,
and job growth.” Autonomy Institute https://youtu.be/9-w0G7sD8NQ
(September 2021) Attack on GPS the Next 9-11? - Video Report KPIX News, San Francisco:
This four minute piece from the CBS affiliate in San Francisco poses an interesting question.
There are certainly plenty of individuals, groups, and governments out there who might like to bring the U.S. to its knees.
For example, in 1996 China suffered what their military calls "The Unforgettable Humiliation" when they lost two of their missiles in flight because,
they say, the U.S. interfered with GPS signals.
China then labored for 24 years to build Bei Dou and make themselves independent of U.S.
satnav. They also made themselves independent of space for PNT
with services from eLoran, a combination of fiber and 5G, and other
systems.
So now that they don't need GPS or space for PNT, maybe it's time for some payback for the humiliation with an attack on GPS. It might be seen by many
in China as fitting. And maybe it could be done in a way that can't be traced back to them.
Or maybe China holds GPS hostage and trades it for something they want, like Taiwan, or the South China Sea.
With America so vulnerable, the future holds a wealth of possibilities for our adversaries.
Our thanks to Molly McCrea at KPIX. She has reported on GPS vulnerability before and also produced this story.
KPIX Original Report: Next 911 Could Be A Cyberattack On Vulnerable GPS Systems Program:
KPIX 5 News EveningCategories: News, Technology & Computing, Local News,
KPIXTV, Top Story, Google
As the nation marks the 20th anniversary of the 911 terror attack on U.S. soil, Juliette Goodrich tells of another growing security threat leaving us
vulnerable to catastrophe.
CLICK IMAGE OR HERE FOR VIDEO: https://sanfrancisco.cbslocal.com/video/5991674-kpix-original-report-next-911-could-be-a-cyberattack-on-vulnerable-gps-systems/
Bathymetric surveys dip into Dead Sea - GPS World:
https://www.gpsworld.com/bathymetric-surveys-dip-into-dead-sea/'
(September 2021) Strengthening PNT to Avert Economic Setbacks - GW Prime:
Blog Editor's Note: A good overview article.
One note, though. The $1.3B loss per day shown for the U.S. should we be without GPS comes from an
RTI study done for the National Institute of
Standards and Technology. That seems like a big loss that we should act to prevent (and we should).
But U.S. GPD is about $63B/day. So that means the RTI study says that if we lose GPS, our economy will only suffer by 2%.
Does that amount seem way low to you? It does to us.
Strengthening PNT to Avert Economic Setbacks
Resilient PNT is neither a particular technology nor a service; it is actually
a combination of many things, depending on the scale and scope of
applications and systems.
By Ananya Narain
Director | GW Consulting
The world we live in today is critically dependent on Positioning, Navigation and
Timing (PNT) services provided by the Global Navigation
Satellite System (GNSS).
Of course, the Global Positioning System (GPS), developed by the US, is the most widely used technology. Apart from commercial operations, we heavily rely on
PNT
services for national security and critical infrastructure applications. From squadron coordinates for military missions, precise location data for search and rescue
operations, scientific pursuits for environmental and disaster monitoring to increasing efficiency and productivity in areas like construction, oil and gas, and mining,
everything runs on PNT. Perhaps that is why the value of these services is growing by the day. However, the heightened reliance on these services can lead to
socio-economic losses as these systems are prone to disruptions, interruptions, and manipulations.
READ MORE: https://www.gwprime.geospatialworld.net/technology-and-innovation/strengthening-pnt-to-avert-economic-setbacks/
(September 2021) DARPA awards Lockheed Martin $25 million contract modification for integration of Blackjack satellites -
SpaceNews:
LockheedMartin is the satellite integrator for Blackjack, a project to
demonstrate the capabilities of small satellites in low Earth orbit for #military
communications, missile warning and navigation.
https://spacenews.com/darpa-awards-lockheed-martin-25-million-contract-modification-for-integration-of-blackjack-satellites/
(September 2021) Sensors to be used in NASA space applications are characterized in:
https://www.nasa.gov/smallsat-institute/sst-soa-2020/guidance-navigation-and-control
General principles applicable in the space application domain are covered in State of the Art of Small Spacecraft Technology:
https://www.nasa.gov/smallsat-institute/sst-soa-2020
(September 2021) Time to Build. Intelligent, autonomous, and electrified infrastructure is the equivalent of the atomic energy race of the
1940s:
National sovereignty and global productivity will go to the nation that deploys the Intelligent Infrastructure supporting Industry 4.0. Unleashing the largest productivity boom in world history. Autonomy Institute
https://youtu.be/9-w0G7sD8NQ
(September 2021) Could a GPS 9/11 Happen? - Location Business News:
By Kevin Dennehy
September 15, 2021
More industry experts are calling for backups to the Global Positioning System as the
20th anniversary of the 9/11 terror attacks recently passed. This
week, in an interview with a San Francisco television station, both former U.S. Secretary of Defense Leon
Panetta, industry expert Dana Goward and others
said a major disaster could be on the horizon if GPS is not protected!
Goward, who is president of the Resilient Navigation & Timing Foundation, doesn’t think the U.S. government is
doing enough to protect GPS’ signal and
satellites. “Absolutely not. Twenty years ago, a government report issued just before 9-11 that called for a series of measures to protect GPS frequencies,
toughen receivers, and provide alternate sources of timing and location information,” he said.
“These have never been seriously acted upon.”
In fact, Goward believes that the situation today is worse than it was in September 2001. “Over the last two decades, the
FCC has significantly reduced
its enforcement staff and its ability to detect and deter disruptions,” he said.
“The FCC decision in the Ligado Networks case has, according to the
executive branch, authorized substantial interference with GPS signals for many users. And
in 2010 when the Loran navigation and timing system was
shutdown, instead of being upgraded as promised, we lost the only widely and publicly available alternative system.”
READ MORE: https://locationbusinessnews.com/could-a-gps-9-11-happen
(September 2021) Engineering various sources of loss provides new features for perfect light absorption:
Natural and manmade physical structures all lose energy, and scientists work hard to eliminate that loss or compensate for it. Optical and photonic
devices lose energy through light scattering, radiation, or material absorption. In some situations, however, intentionally yet carefully designing
loss in open optical devices and systems can lead to unconventional physical phenomena which inspires novel methods for optical control and engineering.
https://engineering.wustl.edu/news/2021/Engineering-various-sources-of-loss-provides-new-features-for-perfect-light-absorption.html
(September 2021) Galileo, OneWeb and the UK’s sovereignty way forward - GPS World:
September 15, 2021 - By Dana Goward
A discussion with Admiral Lord West
Admiral Lord Alan West of Spithead has served the United Kingdom as First Sea Lord and led the government’s efforts for counter terrorism and cybersecurity.
He has been a member of the House of Lords since 2007 and has stayed engaged with defence and maritime issues.
RNT Foundation President Dana A. Goward
spoke with him in early September about the UK’s way forward for GPS-like
services.
DG: The UK government has been talking for years about the nation’s vulnerability to disruption of space-based signals such as those from
GPS and Galileo.
What is being done about it?
LW: Unfortunately, the government is not being as transparent as we might like on this. I do know from comments made in the House of Lords that there is
a group developing a strategy. Also, that the Cabinet Office — our equivalent of the National Security Council in the United States — is deciding who is
to be in charge and how things will be run.
I have heard the strategy group will propose a mix of technologies such as has been discussed in the United
States. The idea of having several different
systems, I am sure, is so that something interfering with one won’t disrupt them all.
This is all supposed to published in November. But I am concerned that government distractions with
COVID, Afghanistan, and other issues will delay that.
DG: What about the OneWeb project? That doesn’t seem to be waiting for a November announcement. And
there is talk it may provide GPS-like timing and
navigation services.
LW: OneWeb is moving forward, but at present it is only about 5G and making it available more quickly and
broadly. There may be a OneWeb Phase 2 that
includes modified or additional satellites to provide positioning,
navigation, and timing (PNT), but that is to be decided.
Admiral Sir Alan West, then First Sea Lord, is pictured with the official chart of anchorages for the International Fleet Review. (Photo: DP Kilfeather’s
book Trafalgar 200 Through the Lens, Queen Elizabeth II 80th Birthday Edition, CC BY-SA 2.5)
DG: How about the UK rejoining Galileo?
LW: Actually, that makes a lot of sense from a practical point of view for both the UK and Europe. Unfortunately, there were a lot of hurt feelings on
the continent with Brexit, some EU leaders seemed to be in punishment mode, and expulsion from Galileo was part of the fallout.
I think that in due course
as tempers cool, we will fully re-engage with the European Space Agency.
DG: So, no UK project for a GPS equivalent?
LW: The government allocated £90 million to that, which enabled a thorough look at the idea but was woefully inadequate to even start a project. Doing a
British version of GPS or Galileo would be hugely expensive and doesn’t make
sense. There are better, cheaper ways of getting what we need.
DG: And what does the UK need? What is the goal?
LW: We need several things.
First, we need a global capability that is ours, or that we are closely partnered in, to support the UK’s worldwide military and economic interests.
We also need to have something in place so that, even if space is denied to us — and that is getting to be more and more of a threat each day — we can
keep our industries, critical infrastructure and economy going at home.
And third, we need a resilient PNT capability as a foundation for current
applications, and to build on for such things as autonomy, intelligent
transportation, and the like.
DG: So how do you get there?
LW: For the global bit, the OneWeb, and perhaps an even closer partnership with the United States on
GPS.
At home, we definitely need a sovereign capability for when space is denied by solar weather or our adversaries. Also to be a check on space signals
because our adversaries and criminals are spoofing them more and more.
I have always thought eLoran was a good choice. The UK pioneered its development and had the world’s first operational system in
2015. It is really
hard to interfere with the signal, and there are other features that could be added to it that would make it even more
robust.
There was a very interesting report called MarRINav ( https://marrinav.com/marrinav-reports/
)
put out last year about what UK maritime needs to ensure it can navigate regardless of whether
the satellites are working or not. They came up with a reasonably inexpensive combination of systems anchored by eLoran.
By the way, it is interesting that the MarRINav study was funded by the European Space Agency. They seem to understand that satellites are not the be
all and end all for PNT services.
DG: That all seems pretty straightforward and the right thing to do. What’s standing in the way?
LW: Well, so few people understand the problem. The population as a whole is almost completely unaware. At some level government understands all 13
of our critical infrastructure sectors could be impacted, but the people senior enough to drive action have dozens of other issues to deal with that
probably seem more urgent.
DG: I wonder what it will take to make it seem urgent enough.
LW: Let’s hope the wakeup call is something short of a national disaster.
(September 2021) UK’s Future Force To Lean Heavily Into Robotics, AI & Hybrid Power:
The British Army is leaning heavily into robotics, ai and hybrid-power technology as part of a new acquisition process dubbed Mercury, according to a
British Army leader involved in future procurement planning.
The Army is grappling with how to acquire technologies that it believes it will need in the future, how to spiral in those technologies across its
equipment programs and how to cultivate skills in its soldiers to use capabilities as they come online.
"Driving innovation to achieve its goals, the Army must better identify technologies that will likely change the way the service operates and fights",
Col. Christopher Coton, the service’s assistant head for concepts, said at the
DSEI defense exhibition in London on Sept. 15, 2021.
(September 2021) Space Systems Command declares three GPS III space vehicles 'Available for Launch' - GPS World:
https://www.gpsworld.com/space-systems-command-declares-three-gps-iii-space-vehicles-available-for-launch/
(September 2021) Air Force begins construction of simulation and wargaming facility for space and lasers:
https://www.c4isrnet.com/battlefield-tech/space/2021/09/16/air-force-begins-construction-of-simulation-and-wargaming-facility-for-space-and-lasers/?utm_source=facebook.com&utm_campaign=Socialflow+DFN&utm_medium=social&utm_campaign=Socialflow+DFN&utm_source=Linkedin&utm_medium=social
https://trib.al/NMWkRUr
(September 2021) Raytheon buys another fast-growing Colorado space company - Denver Business Journal:
https://www.bizjournals.com/denver/news/2021/09/15/raytheon-space-seakr-blue-canyon-small-satellite.html
(September 2021) GPS Lessons from Before 9/11 Still Endanger the U.S. -
Nextgov:.
By Dana A. Goward,
President, Resilient Navigation and Timing Foundation
SEPTEMBER 16, 2021 02:16 PM ET
“Public policy must ensure, primarily, that safety is maintained even in the event of loss of GPS,” officials wrote in the 2001 Volpe Report.
Secretary of Transportation Norman Mineta hefted the report in his hand. Three years in the making, it described America’s over-reliance on the Global
Positioning System and what should be done about it.
This was important. He wanted to read and understand it better before it was made available to the public. So, although the report was dated Aug. 29, 2001,
it wasn’t released until Sept. 10.
The next day the world changed. And the report’s calls for immediate and specific actions across government to protect
GPS and its users were put on the
back burner.
The 2001 Volpe Study’s Warning About GPS
“Critical infrastructure” first emerged as a federal term of art in 1996 when President Bill Clinton established a commission to figure out what it was
and how to protect it. As part of its findings the commission noted transportation’s increasing reliance on GPS, especially in aviation, and recommended
a closer look.
The result was a 113-page document by DOT’s John A. Volpe National Transportation Systems Center published in
2001.
Considering today’s lack of protection for frequencies, vulnerable receivers and the absence of widely available alternatives to GPS, one might be tempted
to think these problems were neither known nor envisioned 20 years ago.
A quick glance at the Volpe report shows just the opposite.
Its assessment of system vulnerabilities, threats and potential severe consequences could have been written today.
Problems with accidental interference and deliberate jamming were well-known and documented. Spoofing and “hazardously misleading information” were listed
as likely to be a problem. And while a direct attack on the GPS Operational Control Segment and/or satellites was seen as less likely, total system loss
for one reason or another was contemplated.
Almost all the report’s recommendations also apply today nearly as much as they did 20 years ago.
It’s very first recommendation began: “Public policy must ensure, primarily, that safety is maintained even in the event of loss of GPS.”
The report went on to discuss the need for things like risk assessment, protecting frequencies through regulation and interference detection, improving
signals, toughening receivers, and the need for backup systems.
About the last it said: “Backups for positioning and precision timing are necessary for all GPS applications involving the potential for life-threatening
situations or major economic or environmental impacts.”
Through the Lens of 9/11
After the attacks of 9/11, the government’s response to the Volpe report was understandably delayed.
When it did come in 2004, officials viewed the report as much through a lens of national security as much as the original focus of fostering transportation
safety and protecting the economy.
This was reflected in December 2004’s National Security President Directive- (NSPD) 39 which assigned a wide variety of GPS-related duties to various
federal departments and agencies. These included:
Good spectrum management to protect GPS frequencies.
Detection, location, attribution of interference, along enforcement actions to deter future events.
Development of a GPS alternative by the Defense Department to be used for national security, and
Acquisition of GPS backup capabilities to support “…critical transportation, homeland security, and other critical civil and commercial infrastructure …”
by the Transportation Department.
With the unclassified portion at only 13 pages and signed by the president, NSPD- 39 was, for a government document, a concise set of orders to protect
the nation.
It came at a time when the pain of an attack on the homeland was still palpable. And when the twin humiliations of failed intelligence, and failure to
take simple anti-hijacking precautions like hardening cockpit doors were still keenly felt.
One would have expected prompt and decisive action to put the president’s orders into effect.
20 Years of Inaction and Regression
Yet 20 years after the first comprehensive official warnings about GPS vulnerability, America has still failed to act.
In fact, rather than moving forward, in some areas we have regressed.
Instead of being careful to protect GPS frequencies, the Federal Communications
Commission (FCC) has licensed operations that many say will interfere
with GPS signals.
And rather than improving its ability to detect violations and act against jammers and spoofers, the
FCC has reduced staff and equipment.
GPS alternative projects within the Department of Defense are still in the science- project
stage. The Government Accountability Office reports those
efforts don’t have the support of senior leadership and often die often or
"die on the vine".
And despite nearly a dozen studies, a law requiring establishment of a national alternative for
GPS timing, and public promises by two administrations
to create a backup system, nothing has been done. Worse, a national alternative system used by some telecom and other industries was terminated
in 2010 against the recommendation of nearly every engineer and technologist in government.
Structured to Fail
The reasons for inaction and backward movement on these issues over the decades are many and varied.
Responsibility for positioning, navigation, and timing (PNT), issues is divided between a variety of departments. Authority to make real changes was
reserved for officials at the Executive Office of the President who typically have neither the expertise nor time to deal with such issues.
GPS services have been generally reliable with no major incident to highlight vulnerabilities. In the absence of a media- worthy event, busy bureaucrats
and political leaders have not had to focus on the threat.
And when it comes to alternatives, advocacy within government and by defense contractors for
GPS-related programs has been vigorous. As is the case with
any major project, efforts that might seem to compete with it or reduce its priority have faced major uphill challenges.
So, rather than being propelled forward as critical to our nation’s well-being, these issues have languished and America’s capabilities have atrophied.
Dangers Increasing
All while China, Russia, Iran, and others have added satellite PNT capability and/or upgraded terrestrial systems that can work with GPS and stand in for
it when it is not available.
They have gained huge tactical and strategic advantages over America by using the last two decades to actually do the things we have only talked about.
Some analysts have opined that GPS is the highest priority target for those who would do America harm, from lone wolf hackers to hostile nations.
And many think it is time to “get the bullseye off GPS” with complementary and backup systems and restore America’s place in the world as PNT leader.
Failing to do so will leave the cockpit doors open to nearly everyone, and the nation vulnerable to another devastating attack.
Dana A. Goward is president of the Resilient Navigation and Timing Foundation.
READ AT NEXTGOV: https://www.nextgov.com/ideas/2021/09/gps-lessons-911-still-endanger-us/185400/
(September 2021) How should we secure PNT resilience? - GPS World Editorial Advisory Board:
Blog Editor's Note: There is a lot to unpack in the three short responses to the question posted to the panel.
Our response to their answers is "all of the above." We absolutely need A holistic approach that includes interference detection and mitigation,
widespread use of more robust receivers, and multiple complementary alternatives.
Budgeteers often look for a single, quick, and inexpensive fix to a given. Good luck with that.
There is no quick fix for a thirty year addiction to a single source of wireless precise time and location. Take the patient abruptly off the drug an
he suffers severely or dies. Rather, you have to make the drug less harmful, the patient stronger, and provide alternative medicines in case the primary
one is not available or doesn't provide all the patient needs.
PNT is one of those really important national services that requires continual leadership and management.
We have failed as a nation to do this and are
in in great danger as a result.
EAB Q&A: How should we secure PNT resilience?:
September 13, 2021 - By Tracy Cozzens
Two decades ago, the Volpe National Transportation System Center released its landmark report on the vulnerability of
GPS. Have this study and its many
successors helped move us to the necessary levels of PNT resilience? Have we done enough? What is left to be done?
READ MORE AT GPS WORLD: https://www.gpsworld.com/eab-qa-how-should-we-secure-pnt-resilience/
(September 2021) Johns Hopkins APL Scientists Contribute Award-Winning Breakthrough to AI-Driven Climate Initiative:
https://www.jhuapl.edu/PressRelease/210917-apl-climate-trace-team-wins-award
(September 2021) U.S. generals planning for a space war they see as all but inevitable -
SpaceNews:
Blog Editor's Note: If you really need electricity and there is a chance the electrical grid might go down, you get a generator... If there is a
chance your ship will be torpedoed, you make sure you have a lifeboat... If you might not have
PNT from space...
There is no space system that is as important to the well being of the United States as the
Global Positioning System (GPS).
If military commanders and politicians are looking at GPS as just another weapons system, we are in deep trouble.
U.S. generals planning for a space war they see as all but inevitable
by Sandra Erwin — September 17, 2021
A ship in the Pacific Ocean carrying a high-power laser takes aim at a U.S. spy satellite, blinding its sensors and
denying the United States critical
eyes in the sky.
This is one scenario that military officials and civilian leaders fear could lead to escalation and wider conflict as rival nations like China and Russia
step up development and deployments of anti-satellite weapons.
If a satellite came under attack, depending on the circumstances, “the appropriate measures can be taken,” said Lt. Gen. John Shaw, deputy commander of
U.S. Space Command.
READ MORE: https://spacenews.com/u-s-generals-planning-for-a-space-war-they-see-as-all-but-inevitable/
(September 2021) How quickly do algorithms improve?:
Algorithms are sort of like a parent to a computer. They tell the computer how to make sense of information so they can, in turn, make something useful
out of it. The more efficient the algorithm, the less work the computer has to do. For all of the technological progress in computing hardware, and the
much debated lifespan of "Moore’s Law", computer performance is only one side of the picture. Behind the scenes a second trend is happening: Algorithms
are being improved, so in turn less computing power is needed. While algorithmic efficiency may have less of a spotlight, you’d definitely notice if
your trusty search engine suddenly became one-tenth as fast, or if moving through big datasets felt like wading through sludge.
How quickly do algorithms improve?
MIT scientists show how fast algorithms are improving across a broad range of examples, demonstrating their critical importance in advancing computing.
https://news.mit.edu/2021/how-quickly-do-algorithms-improve-0920
(September 2021) The Mars helicopter: What’s it up to now?:
Having established that it can fly in the Martian atmosphere and having achieved all its own test objectives,
its role is now scouting out routes for its big brother,
Perseverance rover.
https://www.gpsworld.com/the-mars-helicopter-whats-it-up-to-now/
(September 2021) GPS Disruption Warning - U.S. Maritime Administration:
Blog Editor's Note: This is the most recent warning issued for GPS disruption by the U.S. Maritime Administration
(MARAD). For most of the last four or
five years, MARAD has had a similar warning active and on the books.
The advisory points out that this is a worldwide problem, but is especially a concern in the eastern
Mediterranean. We recommend perusing the
Coast Guard website, where all the reports are listed. Most are in the
Eastern Med, but we think you will be surprised by the wide and interesting distribution of
others.
Note that while this is a warning about GPS disruption, other GNSS are likely impacted
also. Most of the world's jammers don't discriminate between systems
and interfere with most satnavs.
2021-010-Various-GPS Interference
Description
This revised advisory cancels U.S. Maritime Advisory 2021-004
1. Reference: None.
2. Issue: Instances of significant GPS interference have been reported worldwide in the maritime domain. This interference is resulting in lost or
inaccurate GPS signals affecting bridge navigation, GPS-based
timing, and communications equipment (include satellite communications equipment).
Over the last six months, areas from which multiple instances have been reported include the eastern and central Mediterranean Sea and in the vicinity of
the Suez Canal. The U.S. Coast Guard Navigation Center (NAVCEN) web page,
https://go.usa.gov/xMZ2q , contains a chronological list of
recently reported
GPS problems.
3. Guidance: Exercise caution when underway and prior to getting underway. The
NAVCEN and NATO Shipping Center websites contain information regarding
effective navigation practices for vessels experiencing GPS disruption. The information reaffirms safe navigation practices when experiencing
GPS disruptions, provides useful details on reporting disruptions, and is intended to generate further discussion within the maritime community about
other disruption mitigation practices and procedures. This guidance also recommends reporting such incidents in real time; noting critical information
such as the location (latitude/longitude), date, time, and duration of the outage/disruption; and providing photographs or screen shots of equipment failures
failures experienced to facilitate analysis.
The NAVCEN information is available at:
https://mariners.coastguard.blog/2017/09/21/9212017-good-navigation-practices-how-one-vessel-master-managed-safe-navigation-during-a-gps-outage/
4. Contact Information: Maritime GPS disruptions or anomalies should be reported immediately to the
NAVCEN at
https://go.usa.gov/xQBaw
or via phone at 703-313-5900, 24-hours a day. NAVCEN will further disseminate reported instances of GPS interference in this region to the NATO Shipping
Center.
5. Cancellation: This message will automatically expire on March 14, 2022.
For more information about U.S. Maritime Alerts and Advisories, including subscription
details, please visit https://go.usa.gov/xMZTS
LINK TO THE ADVISORY ON THE MARAD SITE: https://www.maritime.dot.gov/msci/2021-010-various-gps-interference
(September 2021) Air Force’s top civilian hints at changes to hypersonic weapons programs:
https://www.defensenews.com/air/2021/09/22/air-forces-top-civilian-hints-at-changes-to-hypersonic-weapons-programs/?utm_source=facebook.com&utm_campaign=Socialflow+DFN&utm_medium=social&utm_campaign=Socialflow+DFN&utm_medium=social&utm_source=Linkedin
(September 2021) Op-Ed: Australia's First Nuclear Sub Project Comes With Big Risks:
https://www.maritime-executive.com/editorials/op-ed-australia-s-first-nuclear-sub-project-comes-with-big-risks
(September 2021) A New Understanding of Galaxy Evolution with NASA’s Roman Space Telescope:
When NASA’s Nancy Grace Roman Space Telescope launches in the
mid-2020s, it will revolutionize astronomy by providing a panoramic field of view
at least 100 times greater than Hubble's at similar image sharpness, or resolution. The
Roman Space Telescope will survey the sky up to thousands of
times faster than can be done with Hubble. This combination of wide
field, high resolution, and an efficient survey approach promises new understandings
in many areas, particularly in how galaxies form and evolve over cosmic time. How did the largest structures in the universe assemble? How did our
Milky Way galaxy come to be in its current form? These are among the questions that Roman will help answer. Galaxies are conglomerations of stars, gas,
dust, and dark matter. The largest can span hundreds of thousands of light-years. Many gather together in clusters containing hundreds of galaxies,
while others are relatively isolated
(September 2021) Xona Space Systems fully funds GPS-alternative demo mission -
SpaceNews:
Blog Editor's Note: A big announcement from Xona Space Systems yesterday. - Full disclosure, Xona is an RNTF corporate
member.
This is likely good timing for Xona. Government interest in LEO PNT seems to be growing.
DARPA has a LEO PNT project underway with Northrup Grumman (NG). Last week
NG announced it had received a contract award from DARPA
for Phase 2 of the project. With an in-space demo funded, Xona may have leapfrogged that effort.
Army Futures Command, working with our friend Todd Humphries at the Univ. of Texas Radionavigation Laboratory, has been investigating
LEO PNT by
leveraging commercial satcom constellations.
Congress has also expressed interest in LEO PNT. The House Armed Services Committee has suggested it could be had from, or by partnering with,
commercial providers. See our commentary and a link to the HASC document
here (below).
Clearly the idea of LEO PNT is "of the moment." It is something we heartily support as part of a robust and resilient PNT
architecture. See our
free downloadable graphic here: https://rntfnd.org/wp-content/uploads/RNT-ecosystem_3.29-v4.pdf
Xona Space Systems fully funds GPS-alternative demo mission
by Jason Rainbow — September 22, 2021
TAMPA, Fla. — Californian startup Xona Space Systems has raised $8 million to fully fund an orbital demonstration next year of its navigation
payload,
which aims to provide an alternative to GPS and other global navigation satellite systems.
Early-stage investor MaC Venture Capital and Seraphim Space Investment
Trust, a fund that was recently listed on the London Stock Exchange, led the
funding round.
Xona CEO Brian Manning said it brings the venture’s total funding to $10 million, including $1 million from a pre-seed round and another $1 million
secured in grants.
READ MORE: https://spacenews.com/xona-space-systems-fully-funds-gps-alternative-demo-mission/
Next-Gen Satellite Navigation: Our Investment in Xona Space Systems:
Jim Adler
22 Sep 2021
The space sector is booming. With space tourism stoking public interest to new highs, space solutions are riding a record wave of investment, building
on the $7.6 billion invested in 2020.
The former rocket engineer in me delights at the growing enthusiasm for space, while my current investor self poses the typical nagging questions of
product viability, operational scalability, as well as path to revenue and earnings.
Fortunately, even in crowded markets, there are early-stage startups that offer the complete package — a compelling vision, disruptive tech, a feasible
business model, an experienced team, and a solid path to product-market fit. That’s why I’m truly excited to announce
our investment in Xona Space Systems,
who’s building the next generation of satellite navigation systems.
READ MORE: https://medium.com/toyota-ventures/next-gen-satellite-navigation-our-investment-in-xona-space-systems-bdff7c02f659
(September 2021) NASA and Italy to send first GNSS receiver to the Moon - GPS World:
The innovative GPS and Galileo receiver, provided by Qascom, will experiment with satellite-based positioning on the lunar surface.
https://www.gpsworld.com/nasa-and-italy-to-send-first-gnss-receiver-to-the-moon/
(September 2021) Rolls-Royce’s all-electric aircraft completes first flight:
https://www.businesstraveller.com/business-travel/2021/09/18/rolls-royces-all-electric-aircraft-completes-first-flight/
(September 2021) Here are the cheap counter-drone solutions DoD tested in the Arizona desert:
Here are the cheap counter-drone solutions DoD tested in the Arizona desert:
https://trib.al/toPNVUC
(September 2021) "Revolution in RF Devices: Sphere Phased-Array Antennas":
For the pertinent information on the above topic, please click here
for a Sphere Phased-Array Antenna Brochure.
(September 2021) China to show off its new electronic-attack jet:
https://trib.al/7mT342R
(October 2021) The hazards of mixing RTK bases - GPS World:
In many ways, it is hard to beat single-base RTK. However, there are challenges. Single-base, typically “iono-free” solutions common in today’s
rovers, degrades over the baseline length. https://www.gpsworld.com/the-hazards-of-mixing-rtk-bases/
(October 2021) Europe awards seven contracts for alternative PNT demos - GPS World:
A notice of award was posted Oct. 11 by the European Union for seven contracts to six different companies for demonstration of
non-GNSS positioning,
navigation, or timing solutions.
The awardees are OPNT BV from the Netherlands; Seven Solutions SL from Spain;
SPCTime of France; GMV Aerospace of Spain; Satelles Inc. of the United
states; and Locata Corporation of Australia.
Locata received two separate contract awards: one to demonstrate delivery of time, and the other for positioning.
According to the EU project officer, Ignacio Alcantrailla-Medina, some of the awardees will demonstrate delivery of time, some positioning, and some
both. Locata received separate awards because the company provided separate responses for timing and positioning.
Eleven different companies responded to the tender, according to the announcement. No information was provided on the unsuccessful bidders.
The EU tender for this project was announced in October 2020. The stated goal of the project is
to better understand available non-GNSS PNT technologies.
The intent is to identify potential backups for GNSS during an outage. All offered technologies were required to be able
to operate independently from
and have “no common points of failure with” GNSS.
Alcantrailla-Medina says the demonstration project is expected to last seven and a half
months. As part of this, a public event will be held at the EU’s
Joint Research Center in Ispra, Italy, in March or April, 2022. This will be
followed by a consolidated report on the project in May or June.
This consolidated report will be used in the next edition of the European Radionavigation Plan due out next fall, according to Alcantrailla-Medina.
Companies that did not respond to the EU’s tender or were not selected for a contract can still have information about their products and services
included in the consolidated report, says Alcantrailla-Medina. Now that all contracts for the demonstrations have been awarded, he is open to receiving
the information and can be contacted at:
Ignacio.ALCANTARILLA-MEDINA
European Commission
DG Defence Industry and Space
Unit C2 – Satellite Navigation
Avenue d’Auderghem 45, (BREY 7/297)
B-1049 Brussels/Belgium
e-mail: ignacio.alcantarilla-medina@ec.europa.eu
LINK TO ARTICLE IN GPS WORLD: https://www.gpsworld.com/europe-awards-seven-contracts-for-alternative-pnt-demos/
(October 2021) NGS Beta OPUS released, accepting RTK and post-processed data - GPS World:
This version of OPUS now accepts real-time kinematic data and post-processed GNSS vectors from vendor
software.
https://www.gpsworld.com/ngs-beta-opus-released-accepting-rtk-and-post-processed-data/
(October 2021) These neural networks know what they’re doing:
Researchers at MIT have now shown that a certain type of neural network is able to learn the true cause-and-effect structure of the navigation task
it is being trained to perform. Because these networks can understand the task directly from visual data, they should be more effective than other
neural networks when navigating in a complex environment, like a location with dense trees or rapidly changing weather conditions. In the future,
this work could improve the reliability and trustworthiness of machine learning agents that are performing
high-stakes tasks, like driving an
autonomous vehicle on a busy highway.
https://news.mit.edu/2021/cause-effect-neural-networks-1014
(October 2021) RNT Foundation proposes attributes for resilient timing RFP - GPS World:
RNT Foundation proposes attributes for resilient timing RFP
October 14, 2021 - By Dana Goward
The Resilient Navigation and Timing (RNT) Foundation has published a white paper proposing attributes for a government Request for Proposal (RFP)
to acquire timing services.
“A National Resilient Timing Architecture – Now for an RFP!” builds upon the foundation’s October 2020 white paper “A Resilient National Timing
Architecture.”
Timing services, most of which are now sourced directly or indirectly from GPS, are essential for myriads of network, transportation, financial, industrial,
and other applications. The National Timing Resilience and Security
Act of 2018 (NTRSA) requires establishment of one or more systems to serve as
alternatives and back up GPS timing.
The RNT Foundation’s October 2020 white paper discusses how a national timing architecture fulfilling the requirements of
NTRSA could be established
relatively easily and inexpensively. It proposes that, rather than building its own system, the government contract for services with commercial providers.
The new white paper outlines some of the requirements and evaluation criteria the government might use when acquiring timing services.
Goals
The paper postulates that the goal of such a procurement should be to establish a federal timing “backbone.” This would fulfill the requirements of NTRSA,
which recognizes that timing is critical for many applications and is also the basis for most electronic positioning and navigation systems.
Establishing this backbone will provide users with an alternative and a safety net for GPS
disruptions, and at other times enable more resilient and
reliable services. As a backbone, it would provide basic, foundational services upon which others would be able to build. The new services would be
expected to:
support a wide variety of public and private applications across the nation
be entirely independent from and have minimal or no common failure modes with
GPS and other GNSS
-provide multiple and diverse methods of timing delivery
-serve both fixed and mobile users.
-Regarding this last point, the paper notes that mobile devices must know their location before they can make use of timing signals.
Thus, the selected
system or combination of systems also will have to provide GPS-independent location information at a basic level to mobile users.
Requirements
Successful proposals, the paper envisions, will need to meet a number of requirements including
serving the entire U.S. land area, airspace, and coastal waters to about 200 miles offshore
enabling all fixed and mobile users to access at least one non-space-based source (to ensure no common failure modes with
GPS/ GNSS)
timing accuracy in all locations to within 500 nanoseconds of universal
coordinated time (UTC); this accuracy should be within 100 nanoseconds of
UTC for
the 50 largest metropolitan areas
one or more integrity measures to provide users confidence in system(s) accuracy
a very high rate of continuity and availability, similar to that of navigation beacons for aircraft
a performance monitoring and control system.
Evaluation Criteria
Fortunately for the government, numerous systems and companies are already able to provide the needed services. Deciding which to select will likely be
a significant effort. Some of the evaluation criteria suggested by the RNT Foundation white paper are:
Annual Cost – While cost will not be the only consideration in this acquisition, the government always has a responsibility to taxpayers to weigh it as
an important factor.
Infrastructure Required Per Unit of Coverage Area – This has been cited by the Department of Transportation as a very important consideration. Not only
does the amount of infrastructure affect cost, but it also has implications for environmental and community impacts.
Spectrum – Signal disruption by in-band and out-of-band transmissions has been a significant issue for GPS. New PNT wireless and radio-frequency services
should pose as few spectrum concerns as possible. Spectrum band reservations, licenses, pre-allocated bands, other bands and adjacent band uses will all
be given consideration.
Penetration – While the government may not list this as a requirement, the ability of a service to reach underwater, underground and indoor locations will
likely be desirable and part of proposal evaluation.
Resilience – The vulnerability of GPS signals to disruption will undoubtedly make the resilience of potential backup and complementary systems a major
issue. The RNT Foundation paper discusses two kinds of resilience – operational and recovery.
Operational resilience is defined as “the ability of a system, combination of systems, or service to resist disruption (e.g.: jamming, spoofing, physical
damage negatively impacting service).” One measure of resilience might be the energy needed to disrupt signals.
Recovery resilience is described as “The speed and ease with which a service can return to normal operation” after a disruption.
Cybersecurity – Similarly, cybersecurity is seen as having two components. The first is network security, defined as the degree to which systems are
isolated from or connected to networks. Second is signal security, and is how well signals can be protected from infiltration and imitation.
Endorsements for GPS Alternative Timing
Since the “National Resilient Timing Architecture” white paper was issued in 2020, calls for
GPS alternatives have intensified, and the white paper itself
has received an important endorsement.
On May 7, the telecommunications industry standards group Alliance for Telecommunications
Industry Solutions (ATIS) vigorously supported federal funding
for GPS alternatives. In letters to leaders in both houses of Congress, ATIS cited “the urgent need for funding the deployment and adoption of Alternative
Positioning, Navigation, and Timing (PNT) Systems in U.S. critical infrastructure, including the U.S. telecom industry.”
The need for federal support for timing and positioning backups for GPS was also supported by a two-year old study released by RAND Corporation in
May.
While the paper went to great lengths to argue against a duplicate GPS-like capability (something no one has supported to the best of our knowledge), it
quietly suggested federal support for both a national timing system and location services to serve E-911 systems.
Numerous recent media releases from U.S. Space Force have revealed serious military threats to GPS and other space-based systems.
A variety of
killer-satellites, lasers and other weapons have turned space from a sanctuary into a potential battle ground. While not specifically calling for
alternatives to GPS, the Space Force announcements have made it clear the nation needs to “get the bullseye off GPS.” Establishing at least one
terrestrial alternative system similar to those operated by our adversaries will make U.S. satellites and signals much less attractive targets,
according to Greg Winfree, former assistant secretary at the U.S. Department of Transportation.
Federal Funding Needed
Federal funding for improving national timing was specifically supported by a group of CEOs and senior executives from major telecom companies. Acting as
the National Security Telecommunications Advisory Committee (NSTAC), the group’s May report to President Biden discussed GPS vulnerabilities and threats,
and urged establishment of a capability
“…similar to that reflected in the Resilient Navigation and Timing Foundation’s paper entitled A Resilient National Timing Architecture. Further, to
enhance the ability of commercial entities to afford leveraging this architecture, the Administration should appropriate sufficient funds to lay the
foundation for creating this timing architecture, with the Federal Government being the first customer for what will ultimately become a resilient,
interconnected network for PNT delivery.”
Federal funding support is necessary, according to NSTAC, because free GPS services greatly suppress market demand for alternatives.
(October 2021) FAA Fumbled Its Response To a Surge in GPS Jamming - IEEE Spectrum:
Blog Editor's Note: One of the first questions skeptics ask is "When GPS isn't available, why don't aircraft just use the backup network of terrestrial
aviation nav beacons?" - These beacons are called "VORs" and
"DMEs," by the way.
Well, some smaller aircraft don't have anything but GPS to navigate with, other than the pilot using a map and looking outside. And finding your way
with a map and looking out the window isn't as easy as it seems. Especially if you have been relying on GPS to help you for 20 years or more. This is why,
for example, light aircraft regularly accidentally violate restricted airspace around places like the Capitol and White House, and have to be escorted out
before they get too close.
The FAA even allows some aircraft to fly in "instrument" conditions (restricted visibility due to clouds, fog, etc.) with just
GPS for navigation. When
GPS goes out and these folks are in the clouds, they need air traffic controllers to tell them which way to head to get into clear air. That increases
workloads for everyone, controllers and pilots alike, and makes the system more dangerous.
Many larger aircraft can use VOR and DME information to navigate. BUT, their flight management systems aren't able to convert that information to allow
point to point routes. Without GPS they often have to go from one terrestrial beacon to another. So flights are longer, burn more fuel, and are overall
more expensive.
Even for the largest and most sophisticated aircraft, GPS is important. In addition to being the primary nav sensor, it enables a wide variety of
non-navigation cockpit services. Things like finding the closest landing field in an emergency, choosing the right frequencies to talk to air traffic
control for the area the plane is in, coordinating arrival services with the company's personnel and contractors at destinations, etc.
So, for the reasons above and many others, many companies and pilots choose not to fly when GPS equipment is not working properly rather than rely on
backup systems and procedures.
FAA Fumbled Its Response To a Surge in GPS Jamming:
Confusion over stopping military tests had flight controllers fuming
by MARK HARRIS
07 OCT 2021
FAA air traffic controllers supervising flights over Arizona, New Mexico and Texas were confused and frustrated by an increase in military tests that
interfered with GPS signals for civilian aircraft, public records show.
In March and April this year, flight controllers at the Albuquerque Air Route Traffic Control Center filed reports on
NASA's Aviation Safety Reporting
System (ASRS), a forum where aviation professionals can anonymously share near misses and safety tips.
The complaints accused the FAA of denying controllers permission to ask the military to cut short GPS tests adversely affecting commercial and private
aircraft. These so-called "stop buzzer" (or "cease buzzer") requests are supposed to be made by pilots only when a safety-of-flight issue is encountered.
"Aircraft are greatly affected by the GPS jamming and it's not taken seriously by
management," reads one report. "We've been told we can't ask to stop
jamming, and to just put everyone on headings."
READ MORE: https://spectrum.ieee.org/gps-jamming
(October 2021) Implementation of GPS Attacks on DJI Phantom 3 Standard Drone as a Security Vulnerability Test - IEEE
Xplore:
Abstract: An attack on a drone is a technique used to stop or obstruct the drone's working system. These attacks can also be used to determine security
vulnerabilities to drones. The DJI Phantom 3 Standard is a wifi-based quadcopter. In this study, navigation attacks in the form of GPS jamming
and GPS spoofing were carried out on the DJI Phantom 3 Standard drone. The goal of this GPS attack in this study is to determine and analyze
the extent of vulnerability in the DJI Phantom 3 Standard commercial drone GPS. The GPS jamming attack uses jamming signals with the GNU
Radio Companion (GRC) app. For GPS spoofing attacks using GPS-SDR-SIM tools to create fake GPS signals for drones. The
GPS attack in this study
uses the BladeRF X40 Software Defined Radio (SDR) device as the main device. The results of this study indicate that
GPS jamming and GPS spoofing
attacks can disrupt the GPS signal and even make the drone lose control.
READ MORE/ACCESS PAPER: https://ieeexplore.ieee.org/abstract/document/9398386
(October 2021) Improving Accuracy In Satellite Navigation Systems:
https://semiengineering.com/improving-accuracy-in-satellite-navigation-systems/
(October 2021) Senate proposes $15M to develop GPS alternatives - GPS World:
Senate proposes $15M to develop GPS alternatives
October 20, 2021 - By Dana Goward
This week Sen. Patrick Leahy (D-Vt.), chair of the Senate Appropriations
Committee, released that body’s version of nine different appropriations bills.
The accompanying report for the bill to fund the Transportation Department
(DOT) outlines the Senate’s intentions and way forward for establishing
alternatives to GPS.
The report provides $15 million for the fiscal year that began on the first of October “to establish a program that leads to wide adoption of multiple
technologies that provide the necessary GPS backup and complementary PNT as identified by the Department’s
report.”
The department report referenced was on a demonstration project that examined GPS backup and complementary technologies from 11 different
vendors. That
DOT report found, based on the technologies demonstrated, a combination of signals delivered from space, terrestrial low frequency
(LF) and ultra-high
frequency (UHF) broadcasts, and fiber would best meet the nation’s needs.
The Senate report accompanying the funding bill outlines components of the GPS alternatives program, including:
development of safety-critical PNT requirements and standards,
user adoption models to facilitate responsible use of resilient PNT, and
procurement of services deemed appropriate by the department.
The Senate Committee report can be found here. Relevant provisions are on page 12.
Services Contracts
While not setting a deadline for issuance of a Request for Proposal, the mention of procuring services is seen by many as a strong indication that
Congress expects more than just additional studies.
Services contracts, as opposed to the government building its own system, have long been advocated by numerous members of industry and by the Resilient
Navigation and Timing Foundation. Contracting for services with commercial providers is a better model, they have argued, as the needed technologies are
mature and commercially available. Also, issuing one or more services contracts would avoid the need for the huge funding lines and lengthy delays
inherent in a government major systems acquisition.
Many have suggested that services contracts would also be a much more economical approach for the government. They say commercial interests can operate
their systems more efficiently, and that they could offer additional services to other customers, potentially reducing costs to the government.
ADS-B Sets Example
Such an approach was used by the Federal Aviation Administration
(FAA) for the ADS-B air traffic safety and management system. The
FAA needed to monitor
and use signals from ADS-B equipment aboard a wide variety of aircraft flying in U.S.
airspace. Rather than building a nation-wide ground infrastructure,
the FAA issued a long-term service contract for a company to collect and provide the signals. The awardee,
Exelis (now L3Harris), won the contract, built
the infrastructure, and now provides ADS-B information to the FAA and others on a subscription basis.
Most observers expect the portions of the Senate bill and report about the GPS alternatives program to be adopted in conference with the House and then
enacted into law.
How far the Department of Transportation will be able to develop the program this fiscal year remains to be seen. The Senate provisions do require
DOT
to report on its progress in a year’s time. Earlier informal reports and updates to the committee are likely to inform funding and other legislation on
this effort for fiscal year 2023.
https://www.gpsworld.com/senate-proposes-15m-to-develop-gps-alternatives/
(October 2021) GNSS & eLoran - European Security and Defence:
Blog Editor's Note: Interesting article that includes quotes from our member Hellen Systems and our colleague
RADM(ret) Nick Lambert, Royal Navy.
One critique. The article states " LORAN has largely fallen out of use..." - Only true
if your whole world is Europe and the U.S.
The world's most populous country (China), and the world's largest and third largest countries by geographic area (Russia and China) have active
Loran systems. They state in public documents these systems are maintained, in part, to guard against losing PNT services if signals from space
are disrupted.
South Korea, Saudi Arabia, and likely Iran all have Loran systems as well.
And the UK has an eLoran transmitter on-line providing wide area, difficult to disrupt timing signals.
So, Loran has NOT fallen out of use, despite the west taking a more cavalier approach to PNT resilience and security.
Global Navigation Satellite Systems
Thomas Withington
Satellite navigation systems are fantastically capable critical national and international
infrastructure, but vulnerable. Fortunately, there is an alternative.
Not since its introduction in 1995 has there been so much focus on the integrity of the US Global
Positioning System (GPS). GPS is one of several Global
Navigation Satellite Systems (GNSSs). Others include the
European Union’s (EU’s) Galileo, the People’s
Republic of China’s (PRC’s) Beidou and Russia’s
GLONASS. GNSS has become essential for navigation over the past three decades. Aircraft, ships and vehicles all use
GNSS to
navigate. The US GPS constellation started life as a Department of
Defence (DoD) project. As a result, US and allied militaries rely heavily on GPS
technology. As a US government website discussing GPS explains “nearly all new military assets, from vehicles to munitions, come equipped with GPS.”
READ MORE - Page 44:
(October 2021) Global GNSS constellations: Why 2 + 2 equals more than 4:
https://www.gpsworld.com/global-gnss-constellations-why-2-2-equals-more-than-4/
Marco Lisi Comment: "The article is correct in highlighting the often underestimated advantages of operating in a multi-constellation environment, but we have to
be careful; it can be demonstrated that beyond four constellations mutual interference would overcome all other benefits.
(October 2021) Facebook chooses u‑blox timing to speed up data centers - GPS World:
By improving the synchronization of networked computers, Facebook’s time card can significantly speed up the performance of its data centers and
distributed databases.
https://www.gpsworld.com/facebook-chooses-u%e2%80%91blox-timing-to-speed-up-data-centers/
(October 2021) U-blox releases u-center 2 GNSS evaluation software - GPS World:
U-center 2 is designed to offer improved performance over its
predecessor, as well as new features that simplify configuration,
evaluation
and software development of GNSS-based solutions.
https://www.gpsworld.com/u-blox-releases-u-center-2-gnss-evaluation-software/
(October 2021) The future of radar: the evolution of a technology with a long history:
https://www.leonardocompany.com/en/news-and-stories-detail/-/detail/the-future-of-radar-the-evolution-of-a-technology-with-a-long-history
Marco Palladini
Managing Director at Diamond Antenna Europe
Conventional non-cooperative 2D primary radars (a 3D radar is not required in civil
ATC because the aircraft height can be determined by the secondary
radar)
used in ATC consist of a fixed microwave power transmitter/receiver and a rotating parabolic antenna.
A RF rotary joint is required to connect the fixed and
rotating sections. This architecture can use two beams, aimed at two different
heights. The lower one can scan more distant regions of space, while the
higher one, closer space. These two beams can provide information for partial clutter reduction. Often only one beam is used.
A linear array antenna can
improve the performance of the radar by turning it into 3D radar and adding the ability to steer the beam in correspondence to the azimuth of specific
obstacles. This radar will still use an RF rotary joint, in addition to
multiple DC signals. The cost of this radar system is competitive compared to an
AESA phased array with TRM modules in antenna that do not require RF rotary joint
anymore, but only slip-ring if the antenna is a single rotating panel
or even with that of an AESA radar with several fixed panels, which does not require any rotary
joint.
DIAMOND ANTENNA's rotary joints are very specific solutions for several #RADAR
systems:
- en-route radar systems,
- Air Surveillance Radar (ASR) systems,
- Precision Approach Radar (PAR) systems,
- surface movement radars,
- weather radars.
Come to visit our booth at World ATM event in Madrid last week of October
2021
DARPA nabs Gremlin drone in midair for first time:
https://www.defensenews.com/unmanned/2021/11/05/darpa-nabs-gremlin-drone-in-midair-for-first-time/?utm_medium=social&utm_source=Linkedin&utm_campaign=Socialflow+DFN
(November 2021)
Don’t let the titanium metal walls or the sapphire windows fool you. It’s what’s on the inside of this small, curious device that could someday kick off
a new era of navigation. For over a year, the avocado-sized vacuum chamber has contained a cloud of atoms at the right conditions for precise navigational
measurements. It is the first device that is small, energy-efficient and reliable enough to potentially move quantum sensors — sensors that use quantum
mechanics to outperform conventional technologies — from the lab into commercial use, said Sandia scientist Peter Schwindt. Sandia developed the chamber
as a core technology for future navigation systems that don’t rely on GPS satellites, Peter said. It was described earlier this year in the journal AVS
Quantum Science.
https://www.sandia.gov/labnews/2021/10/22/this-device-could-usher-in-gps-free-navigation/
(November 2021) L3 Harris Wins $120 Million Contract To Upgrade Space Force Electronic Jammers - Space News:
by Sandra Erwin — October 22, 2021
The Space Force called the Counter Communications System "the first offensive weapon system in the United States Space Force”
WASHINGTON — The U.S. Space Force awarded L3Harris Technologies a $120.7 million contract to upgrade a ground-based communications jammer used to
block adversaries’ satellite transmissions.
The contract, announced Oct. 22, is for upgrades to the Counter Communications System Block 10.2 that currently operates at Peterson Space Force
Base, Colorado; Vandenberg Space Force Base, California; Cape Canaveral Space Force Station, Florida; and classified locations overseas.
READ MORE: https://spacenews.com/l3-harris-wins-120-million-contract-to-upgrade-space-force-electronic-jammers/
(November 2021)
eLoran has been named by numerous studies, including most recently "MarRINav" and the
DOT "Complementary PNT and GPS Backup Technologies Demonstration
Report," as part of the solution.
The overall point, though, regardless of the technology used, has to be "The time to act is now.
This issue has been studied to death for more than 20
years. There are technologies ready to deploy. It is time for action. A failure of national
PNT will be catastrophic.”
Est. reading time: 5 minutes
November 3, 2021 - By Matteo Luccio
Opposite and complementary
Though marvelous, GNSS are also highly vulnerable. eLoran, which has no common failure modes with
GNSS, could provide continuity of essential timing and
navigation services in a crisis.
GPS fits Arthur C. Clarke’s famous third law: “Any sufficiently advanced technology is indistinguishable from magic.” Yet, it also has several well-known
vulnerabilities — including unintentional and intentional RF interference (the latter known as jamming), spoofing, solar flares, the accidental destruction
of satellites by space debris and their intentional destruction in an act of war, system anomalies and failures, and problems with satellite launches and
the ground segment.
Over the past two decades, many reports have been written on these vulnerabilities, and calls have been made to fund and develop complementary positioning,
navigation and timing (PNT) systems. In recent years, as vast sectors of our economy and many of our daily activities have become dependent on
GNSS, these
calls have intensified.
A key component of any continent-wide complementary PNT would be a low-frequency, very high power, ground-based system, because it does not have any common
failure modes with GNSS, which are high-frequency, very low power and space-based. Such a system already exists, in principle: it is
Loran, which was the
international PNT gold standard for almost 50 years prior to GPS becoming operational in 1995. At that point,
Loran-C was scheduled for termination at the
end of 2000.
READ MORE: https://www.gpsworld.com/eloran-part-of-the-solution-to-gnss-vulnerability/
(November 2021) Radiant aims to replace diesel generators with small one-megawatt micro-nuclear reactors with helium coolant!
(November 2021) Space tracking startup Privateer hires Jah as chief scientific adviser -
SpaceNews:
https://spacenews.com/space-tracking-startup-privateer-hires-jah-as-chief-scientific-adviser/
DUBAI, U.A.E. — A space sustainability startup still largely in stealth mode has hired a leading “space environmentalist” as its chief scientific adviser as
it develops satellites to track objects in orbit.
Privateer announced last month it selected Moriba Jah, an associate professor of aerospace engineering at the University of Texas at Austin as its chief
scientific adviser. Jah will remain at the university as he assists the company build up its capabilities.
Hawaii-based Privateer has kept a low profile to date, other than the release of a one-minute video in September that explained that the company was
“working to keep space safe and accessible to all humankind.” The company was a sponsor of the Advanced Maui Optical and Space Surveillance Technologies,
or AMOS, conference in Hawaii that month, but maintained a low profile beyond placing its logo on coffee cups during a break at the conference.
While Privateer was initially thought to be working on orbital debris removal technologies, the company is instead focused on better monitoring of satellites
and other objects in orbit. “We want to focus on decision intelligence,” Jah said in an interview during the 72nd International Astronautical Congress.
“How do we enable these things and do so in a way that makes space more transparent, makes space more predictable and can develop a body of evidence to
help people and hold them accountable for their behaviors.”
Jah has developed AstriaGraph, a visualization tool that combines space situational awareness data from a several sources. AstriaGraph will be the core of
Privateer’s efforts, he said, creating a “multisourced digital commons of stuff in space.”
Privateer will augment that with data from a constellation of satellites it plans to develop. Its first prototype satellite, Pono-1, will launch early next
year. The three-unit cubesat will carry a variety of sensors to track and characterize space objects.
“That’s going to be a demonstrator of some of those things,” such as both optical and
multi-spectral sensors. “Some things are going to work, some things
probably aren’t, and we’ll learn from that.”
Future satellites might grow to six-unit cubesats, he said, but the company seeks to follow the model of Planet, which developed a constellation of imaging
cubesats. “We’re definitely inspired by what Planet has done in proliferated sensing, so that’s something we’re looking at,” he said.
The uses of such data go beyond simply predicting conjunctions, Jah said. It can assist astronomers attempting to mitigate the effects of satellites on
their observations, as well as government agencies working to provide the “continuing supervision” of space activities under Article 6 of the Outer Space
Treaty. Being able to characterize objects with details like their shape and spin rate, he added, can help companies developing technologies to remove
orbital debris.
Some of the data Privateer collects will go into AstriaGraph, he said, which will continue to be freely available. “Some sort of commercial version of that
will be the thing that Privateer offers,” he said, with value-added services on top of the data.
Jah said he was drawn to working with Privateer after discussions with its founders — Alex Fielding, who co-founded technology company Ripcord, and Steve
Wozniak, co-founder of Apple — because of a shared interest in space environmentalism. “They said they want to build Privateer around that, and that meant
a lot to me,” he said.
“We are so proud to have a scientist and human of Moriba’s caliber joining the Privateer team,” Wozniak said in a statement. “His knowledge of this issue
is only exceeded by his passion for building solutions to address it.”
(November 2021) DARPA has caught a Gremlin drone in midair. Can it grab four in a half-hour?:
DARPA has caught a Gremlin drone in midair. Can it grab four in a half-hour?
https://trib.al/bk6DCS4
https://www.defensenews.com/industry/techwatch/2021/11/08/darpa-has-caught-a-gremlin-drone-in-midair-can-it-grab-four-in-a-half-hour/?utm_medium=social&utm_source=Linkedin&utm_campaign=Socialflow+DFN
(November 2021) Congressman to Introduce Webinar on Protecting GPS - DomPrep &
RNTF:
Congressman to Introduce Webinar on Protecting GPS
The Honorable John Garamendi (D-CA) will provide opening remarks for a 17 November webinar co-sponsored by Domestic Preparedness Journal and the Resilient
Navigation and Timing Foundation. Garamendi is the chair of the House Armed Services Readiness Subcommittee and has long been concerned about the
vulnerability of America’s Global Positioning System (GPS).
The webinar will focus on ways to deter attacks on and interference with GPS satellites and
signals.
“America’s over-reliance on GPS makes it a high priority target for a wide range of bad actors,” said Dana A. Goward,
President of the Resilient Navigation
and Timing Foundation, and one of the webinar moderators. “And, since other nations, such as China, Russia, and Iran, have terrestrial systems they can use
when space is not available, the U.S. is at a strategic disadvantage.”
This “technology resilience gap” is one of several dangers that could lead to armed conflict that webinar panelist George Beebe discusses in his book “The
Russia Trap.” His concern is that having such a pronounced relative weakness can invite meddling and exploitation by adversaries. Even if done on a small s
cale, this could lead to a series of escalating responses ending in an unintended, much more serious conflict that neither party wants.
Beebe is Vice President and Director of Studies at the Center for the National Interest. He spent more than two decades in government service as an
intelligence analyst, diplomat, and policy advisor, including service as director of CIA’s Russia analysis, and as Special Advisor to Vice President
Chaney for Russia/Eurasia and Intelligence Programs.
Eliminating the gap between the U.S. and its adversaries is key to protecting GPS and the nation, according to webinar panelist Greg Winfree, Director of
the Texas Transportation Institute. Winfree previously served as an Assistant Secretary for the U.S. Department of Transportation. While acknowledging there
is no single answer, he has asserted that providing at least one alternative system will go a long way toward “getting the bullseye off
GPS.”
The third webinar panelist, Scott Pace, has supported Winfree’s approach. Pace is the Director of George Washington University’s Space Policy Institute and
former Executive Director of the National Space Council. He has commented that having an alternative to
GPS will contribute to national security and improve
global stability. It will “lower the pressure on us to escalate and respond” should
GPS satellites be damaged, or services disrupted.
The webinar will be held on Wednesday the 17th of November from 2:30 PM to 3:30 PM EST. More information is available at
DomesticPreparedness.com.
Attendance is free but attendees must register in advance HERE.
Press contact: 800-522-6948 or inquiries@RNTFnd.org
(November 2021) Protecting GPS Satellites, Signals, and America:
ORGANIZER MESSAGE
Thank you for registering for the Protecting GPS Satellites, Signals, and America
Webinar. We look forward you joining us at 2:30 p.m. (ET) on November 17th.
Please remember to add the Zoom link to your calendar.
DATE:
Wed, Nov 17, 2021 2:30 PM - 3:30 PM EST
Welcome to the Protecting GPS Satellites, Signals, and America Webinar
Please click the link below to join the webinar. The link will be active 30 minutes prior to the meeting. All participants are on a listen only line.
https://tdem-texas-gov.zoom.us/j/88950059784
Or One tap mobile :
US: +13462487799,,88950059784#,,,,*123567#
or +13126266799,,88950059784#,,,,*123567#
Or Telephone:
Dial (for higher quality, dial a number based on your current location):
US: +1 346 248 7799
or +1 312 626 6799
Webinar ID: 889 5005 9784
Press contact: 800-522-6948 or inquiries@RNTFnd.org
(November 2021) Thales inertial navigation system boards French Navy vessel - GPS World:
Thales and CS GROUP partner to offer navies a cybersecure, jam-resistant #navigationsystem inspired by civil aviation. #inertial
https://www.gpsworld.com/thales-inertial-navigation-system-boards-french-navy-vessel/
Another Topic:
https://esto.nasa.gov/project-selections-for-iip-21/
(November 2021) Small satellites:
https://lnkd.in/d-4kQtgm (scroll down to the
4th bullet)
(November 2021) PNT Advisory Board to Meet Dec. 9-10: GPS World:
Blog Editor's Note: All RNT Foundation members are invited to a reception at 5:30 8 December at the same venue as the Advisory Board meeting, and the
Foundation's annual meeting and lunch at noon on the 10th of December at the same location. Both events are free of charge, but members are asked to
RSVP for each to inquiries@RNTFnd.org before 1 December.
PNT Advisory Board to Meet Dec. 9-10
November 12, 2021 - By Dana A. Goward
The U.S. President’s National Space-based Positioning, Navigation and
Timing (PNT) Advisory Board will meet on December 9 and 10 at the Sheraton Pentagon
City Hotel in Arlington, VA, according to a post on the group’s website.
The meeting is open to the public. Interested parties are encouraged to attend.
The agenda, while still not finalized, is expected to include a full day public meeting on Thursday, December 9, and a half day on Friday, December 10.
Previous in-person meetings have included program updates from government departments and briefings on cutting edge government and industry projects on the
first day. The second day normally sees updates from international representatives and open discussion of current issues among the board members.
The Advisory Board’s size is expected to increase at this meeting with three previous members leaving and nine newly appointed members being added.
A formal announcement of the meeting is expected in the Federal Register on Monday, November 15. Confirmation of the new membership roster is expected at
about the same time.
The PNT Advisory Board was established in 2004 by National Presidential Security Directive 39, “U.S. Space-Based Positioning, Navigation, and Timing Policy.
” It operates under the rules of the Federal Advisory Committee Act and is tasked with providing advice “… on U.S. PNT policy, planning, program management,
and funding profiles in relation to the current state of national and international space-based PNT services.”
The Advisory Board has regularly advised the government on all aspects of space-based PNT, including the need for a holistic “PTA” approach – “Protect”
signals, “Toughen” user equipment, and “Augment” services with alternative PNT sources.
This will be the first in-person meeting of the board since November 2019. A virtual meeting was held in July 2020.
After the conclusion of the government Advisory Board meeting on Friday, December 10, the non-profit Resilient Navigation and Timing Foundation will hold
its annual membership meeting and lunch at the same venue.
READ IN GPS WORLD: https://www.gpsworld.com/national-pnt-advisory-board-to-meet-december-9-and-10/
(November 2021) Using MATLAB with Python Video:
https://www.mathworks.com/videos/using-matlab-with-python-1591216182793.html?source=15572&s_eid=psm_15572
November 2021) The only comprehensive & continuously updated directory of leading providers of global navigation satellite system (GNSS) and other
position, navigation and timing (PNT) solutions and services is available year-round. Visit our dedicated Buyers Guide site: gpsworldbuyersguide.com
(November 2021) What Happens If Time Gets Hacked - Dark Reading:
Blog Editor's Note: Interesting report from Black Hat Europe. While this is the first media report we have seen of a low frequency time signal being
spoofed/hacked, it is not surprising. Open systems and signals are vulnerable. Period.
Next gen time signals - terrestrial or satellite, LF, VHF, UHF, or fiber, must be protected and authenticated.
Multiple diverse methods of delivery, resistance to spoofing and cybersecurity are key evaluation criteria in our October 2021 white paper "A Resilient
National Timing Architecture - Now for an RFP!"
The technology is available. We can't imagine anyone would build any other way.
What Happens If Time Gets Hacked
A renowned hardware security expert raises alarm on the risk and dangers of cyberattackers targeting the current time-synchronization infrastructure.
Kelly Jackson Higgins
Executive Editor
BLACK HAT EUROPE 2021 - London - Most people take time synchronization for granted, but it operates on what hardware security expert Adam Laurie calls a
"fragile ecosystem." Laurie, a renowned hardware hacker, here today demonstrated an unnervingly simple way to alter time on a clock.
"I was curious if I could spoof the time" synchronization signal, he explained in a keynote on his research. So he built his own simulated time-signal
system using an open source tool called txtempus, which simulates signals for syncing the time on clocks and watches, and ran it on Raspberry Pi outfitted
with a radio-frequency identification (RFID) antenna.
Laurie's contraption overrode the UK region's official low-frequency, radio broadcast-based clock synchronization signal.
READ MORE: https://www.darkreading.com/vulnerabilities-threats/what-happens-if-time-gets-hacked
(November 2021) OneWeb LEO PNT: Progress or Risky Gamble? - Inside GNSS:
Blog Editor's Note: A very interesting article by Ramsey Faragher and Marek Ziebart.
We have written before about the differences between radionavigation and radiocommunication in conjunction with the
Ligado controversy.
This is a very interesting discussion of the issue when it comes to satellites. Lots of things to consider.
One we hadn't thought of before is how LEO communications satellites rely upon
GNSS. From the article:
"...the OneWeb system currently depends upon GNSS receivers installed within the OneWeb communication
receivers. The OneWeb receivers use
the GNSS PNT solution to determine the current exact location and
time and then use models of the OneWeb orbits to correctly set the correct radio
frequency and frequency rate required by the receiver to acquire and lock onto the current serving OneWeb satellite as it whizzes across the sky with
significant Doppler shift."
Makes perfect sense, when you think about it.
So... LEO PNT from COMSATS, good for GNSS augmentation, but, at the moment,
not good for GNSS alternatives.
https://insidegnss.com/oneweb-leo-pnt-progress-or-risky-gamble/
(November 2021) Air Force seeks to use artificial intelligence (AI) to sift through courses of action in battle planning:
This capability will enable combat planners to reason about plausible outcomes quickly to increase the planners’ confidence in their
ROME, N.Y. – U.S. Air Force battle planning experts will brief industry next month on an upcoming project to revolutionize air operations planning
by using artificial intelligence (AI) to help commanders formulate the best plan possible against strong enemy forces.
Officials of the Air Force Research Laboratory Information Directorate in Rome, N.Y., issued a special notice on Wednesday
(BAA FA8750-22-S-7001)
for the Fight Tonight project.
Air Force experts will brief industry on this program in hybrid virtual and in-person events from 9 a.m. to 5 p.m. on 8 and 9 Dec. 2021. In-person
briefings will be at the Innovare Advancement Center, 592 Hangar Road, in Rome, N.Y. Experts will follow the same agenda each day.
The Fight Tonight program seeks to revolutionize air operations battle planning using
AI in an interactive game engine for building, rehearsing, and
assessing combat plans.
Related: Military researchers to use gaming concepts and artificial
intelligence (AI) for nuanced communications
This capability will enable combat planners to reason about plausible outcomes quickly to increase the planners’ confidence that they have crafted
the best plan possible against peer adversaries.
The goal is to provide a revolutionary capability to enable planners to explore and access plausible futures rapidly to select the best plans. This
will accelerate planning and explore potential courses of action with enhanced by tools that can generate and assess the feasibility of more plans
than humans are capable of formulating on their own.
Goals of the briefings are to promote teaming and provide an opportunity for government and industry to gather more information prior to expected
submission of white papers 10 10 Jan. 2022.
Related: Air Force eyes inexpensive Skyborg unmanned combat aircraft that pushes bounds of
artificial intelligence (AI)
Companies should register online no later than 1 Dec. 2021 at https://app.smartsheet.com/b/form/0fa591c32af04371be5a3966e0033782.
For questions or concerns contact the Air Force's Jeff Hudack by email at jeffrey.hudack@us.af.mil, or by phone at 315-330-4877.
More information is online at https://sam.gov/opp/23aaa38e1a9d458991ab51eb54b5ec05/view.
(November 2021) DJI's Mavic 3 has a better sensor than previous versions, a dual-camera system,
omni-directional obstacle sensing,
smarter flight modes and longer flight times.
https://www.gpsworld.com/djis-new-mavic-3-has-longer-flight-time-obstacle-sensing/
(November 2021) Small, precise and affordable gyroscope for navigating without GPS:
The new resonator and electrodes, on a finger for scale. The resonator is almost perfectly symmetrical, made of nearly-pure glass. This enables it to
vibrate for long periods, similar to the ringing of a wine glass.
https://news.umich.edu/small-precise-and-affordable-gyroscope-for-navigating-without-gps/
(November 2021) RadioWaves, an Infinite Electronics, Inc. brand and a manufacturer of high-quality microwave #antennas and accessories,
has released a new series of GPS/GNSS timing antennas that cover L1 and L5 #GPS bands:
https://www.gpsworld.com/radiowaves-launches-gps-gnss-timing-antennas/
(November 2021) Navy looks to get back on schedule for fielding hypersonic missiles on submarines:
https://www.defensenews.com/naval/2021/11/18/navy-looks-to-get-back-on-schedule-for-fielding-hypersonic-missiles-on-submarines/?utm_campaign=Socialflow+DFN&utm_medium=social&utm_source=facebook.com&utm_source=Linkedin&utm_medium=social&utm_campaign=Socialflow+DFN
(November 2021) U.S. Leaderless in Space? - INSA Paper & SpaceNews
OpEd:
Blog Editor's Notes:
Two different items on the same underlying theme popped up on our radar recently. The first,
an INSA proposal to designate space a critical U.S.
infrastructure. The second an OpEd in SpaceNews by two highly respected analysts lamenting the lack of leadership and coherent American approach
to international space issues.
The INSA proposal is not a new one. Similar proposals have been made to designate space,
PNT, and other sectors as critical infrastructure. We are
not sure the advocates of any of these moves really want the Department of
Homeland Security (DHS) more involved in their worlds. Other departments
might be more knowledgeable and capable of coordinating a whole of government & industry approach.
It is clear, though, that INSA's main message is that space is really
important, government leadership to protect the nation is sorely needed but lacking.
Designating space as critical infrastructure, INSA says, would "Enable the United States to establish a national level
Office of Primary Responsibility
(OPR) with authority and resources to drive interagency efforts."
Yet there is nothing stopping the administration from doing that now.
Nothing, that is, aside from a bureaucratic tradition of ensuring authority and responsibility is retained as close to the White House as possible. That
is why national plans, strategies, and policies for space (and other issues that cut across departments) diffuse responsibility and authority as much as
possible. Doing so ensures that bureaucrats at the Office of Management and Budget and the
National Security Council keep a tight rein on everything and
remain solidly in charge.
Too bad those folks don't have the time or attention to really be in charge of anything since they are distracted by thousands of pressing issues. And too
bad than not designating a lead department ensures no one else is empowered, initiative is crushed, and inaction becomes the order of the day.
So, while we agree that more and better federal leadership is needed, we are not confident that formally designating space as critical infrastructure will
to get us there.
The OpEd in SpaceNews is an interesting discussion of the recent Russian
ASAT and its implications. This piece by a pair of highly respected analysts is
more overt in calling out a shortfall in U.S. government focus and leadership:
"If the U.S. treats this test as a wake-up call and seizes the opportunities available to it, the next couple years could constitute a major turning point
in space security and sustainability. If, however, the U.S. fails to understand Russia’s perspective and recognize the importance of being proactive in
shaping the strategic incentives of potential adversaries, then the future of both the space environment and the international sphere is likely to be much
dimmer."
The below is reposted from the INSA site. Click on the title to go to their page.
A link to the item in SpaceNews is below the INSA item.
https://www.insaonline.org/designating-space-systems-as-new-u-s-critical-infrastructure-sector/
Op-ed | Lessons to learn from Russia’s Nudol ASAT test:
https://spacenews.com/op-ed-lessons-to-learn-from-russias-nudol-asat-test/
(November 2021)
https://insidegnss.com/esa-awards-contract-for-network-assisted-pnt-assurance-involving-iridium/
(November 2021) Just don’t become a pundit. The definition of pundit is one who can appear credible speaking on a variety of subjects without knowledge or
understanding. There is even a training course for pundits in DC. Sadly, Carl Sagan was a pundit. The scientific community shunned him despite his public visibility.
He was denied tenure at Harvard and rejected by the National Academies. His personal life was less than stellar. He spent his time seeking adulation rather that doing science.
(November 2021) When debris disaster strikes:
In 2021 so far, some 2467 new objects large enough to be tracked have been added to world catalogues of orbital objects, out of which
1493 are new
satellites and the rest are debris. While new objects are added, others are dragged down to Earth by the atmosphere where they safely burn up, resulting
in a net increase of at least 1387 trackable objects between 2020 and 2021. In addition,
an estimated 1500 new objects – an increase of about 5% with
respect to the total population – were added just this week, meaning the risk to missions must be reassessed.
https://www.esa.int/Safety_Security/Space_Debris/When_debris_disaster_strikes
(November 2021) Russia destroys satellite in ASAT test:
https://spacenews.com/russia-destroys-satellite-in-asat-test/
(November 2021) 'Lack of GPS Alternative Invites Attack' - Expert Panel:
Domestic Preparedness Journal and RNT Foundation sponsored a webinar last week discussing the geo-political implications of what panel
member George Beebe has called a "technology resilience gap" between the U.S. and its primary adversaries,
China and Russia.
Beebe is the Vice President for Studies at the Center for the National Interest.
That China and Russia have national alternatives to GPS and other GNSS and the US does not is worse than a critical vulnerability. It actually invites
exploitation and attack by those who would do America harm.
Beebe is concerned that the imbalance is so critical it could lead to an escalating series of responses ending in a shooting or even nuclear war.
As part of the panel he outlined the historical bases for his concerns going back over a century and using a pre-WWI technology gap as an
example.
The other panelists, Scott Pace, Director of the Space Studies Institute, and Greg Winfree, Director of the Texas Transportation Institute, shared Beebe's
concerns. Winfree said about establishing a U.S. alternative "We need to get the bullseye off GPS."
An audio recording of the panel is available here (the webinar did not include any slides or video). A link to a video version will be posted here when
available.
https://www.domesticpreparedness.com/podcast/protecting-gps-satellites-signals-and-america-webinar/
(November 2021) The connection between conservation laws and symmetry intrigues me a lot. Have you ever written any article about Noether's Theorem?
https://www.cantorsparadise.com/emmy-noether-and-one-of-the-deepest-observations-in-all-physics-9a975ae755f5?gi=c7b06e522aef
(November 2021) Assured positioning, navigation and timing (#APNT) enable #Autonomy and provide the precision, reliability and robustness required to operate
in denied or degraded #GPS/#GNSS environments:
Read more in our editorial by Hexagon's Autonomy & Positioning division president and CEO Michael Ritter from our
2021 issue of Velocity:
https://hxgn.biz/3C2ANM7
(November 2021) Using MATLAB with Python Video:
https://www.mathworks.com/videos/using-matlab-with-python-1591216182793.html?source=15572&s_eid=psm_15572
(November 2021) Russia destroys satellite in ASAT test:
https://spacenews.com/russia-destroys-satellite-in-asat-test/
(December 2021) Russia issues threat to GPS satellites - GPS World:
Blog Editor's Note: Perhaps this is a prelude to an invasion of Ukraine.
Regardless the Russians are not bluffing. Our intelligence and Space Force folks here in the U.S. say the Russians (and Chinese) can do it.
What's the best way to protect GPS?
Make it a less attractive target by having an alternative that is not subject to the same kinds of attack.
Despite a law mandating such a system, the last administration failed to act.
What will this administration do?
November 29, 2021 - By Tracy Cozzens
The Kremlin warned it could blow up 32 GPS satellites with its new anti-satellite technology,
ASAT, which it tested Nov. 15 on a retired
Soviet Tselina-D satellite, according to numerous news reports.
Russia then claimed on state television that its new ASAT missiles could obliterate
NATO satellites and “blind all their missiles, planes and ships, not to mention
the ground forces,” said Russian Channel One TV host Dmitry Kiselyov, rendering the West’s GPS-guided missiles useless. “It means that if NATO crosses our red
line, it risks losing all 32 of its GPS satellites at once.”
READ MORE: https://www.gpsworld.com/russia-issues-threat-to-gps-satellites/
(November 2021) Assured positioning, navigation and timing (#APNT) enable #Autonomy and provide the precision, reliability and robustness required to operate
in denied or degraded #GPS/#GNSS environments.
Read more in our editorial by Hexagon's Autonomy & Positioning division president and CEO Michael Ritter from our 2021 issue of Velocity >>
https://hxgn.biz/3C2ANM7
(December 2021) Unmanned and AI: Indy Challenge takes autonomous to big track - GPS World:
The Indy Autonomous Challenge has shown advancement in the technology of unmanned vehicles, which could lead to #autonomous cars on our roads.
GNSS
Aerospace's Tony Murfin covers the event and offers his thoughts to GPS
World.
https://lnkd.in/gc5fsRN8
https://www.gpsworld.com/unmanned-and-ai-indy-challenge-takes-autonomous-to-big-track/
(December 2021) New Government UFO Report Hints at Surprising Science:
"But what if UAP's are unlike anything we might build, possessing no internal propulsion system of their own, but relying instead on external sources? Or,
what if these UAPs aren't manufactured objects at all, but a sort of mid-air projections that appear to be solid objects?"
https://www.psychologytoday.com/gb/blog/long-fuse-big-bang/202111/new-government-ufo-report-hints-surprising-science
(December 2021) Galileo OSNMA position opens, TeleOrbit authenticates with Goose - GPS World:
https://www.gpsworld.com/galileo-osnma-position-opens-teleorbit-authenticates-with-goose/
(December 2021) U.S. Satellites Are Being Attacked Every Day According To Space Force General - The Drive:
Blog Editor's Note: America has more satellites in space than any other country. And we are more reliant on satellites for everyday services than any
other country.
Why wouldn't our adversaries across a broad range from disgruntled hacker to "we will bury you" nation state poke at our single point of failure.
If the administration were to obey the law and establish a terrestrial timing system to complement and backup
GPS, that would be one huge worry dealt with.
Doing so could be relatively easy and inexpensive. So let's get on with it.
U.S. Satellites Are Being Attacked Every Day According To Space Force General
Space Force general details how jamming, blinding lasers, cyber attacks, and other satellites have America's space-based capabilities under siege.
BY JOSEPH TREVITHICK, NOVEMBER 30, 2021
U.S. Space Force's General David Thompson, the service's second in command, said last week that Russia and China are launching "reversible attacks," such
as electronic warfare jamming, temporarily blinding optics with lasers, and cyber attacks, on U.S. satellites "every single day." He also disclosed that a
small Russian satellite used to conduct an on-orbit anti-satellite weapon test back in 2019 had first gotten so close to an American one that there were
concerns an actual attack was imminent.
Thompson, who is Vice Chief of Space Operations, disclosed these details to The Washington Post's Josh Rogin in an interview on the sidelines of the
Halifax International Security Forum, which ran from Nov. 19 to 21 in Halifax, Nova Scotia, in Canada. The forum opened just four days after a Russian
anti-satellite weapon test involving a ground-launched interceptor, which destroyed a defunct Soviet-era electronic intelligence satellite and created
a cloud of debris that presents a risk to the International Space Station
(ISS). That test drew widespread condemnation, including from the U.S. government,
and prompted renewed discussion about potential future conflicts in space.
https://www.thedrive.com/the-war-zone/43328/u-s-satellites-are-being-attacked-everyday-according-to-space-force-general
(December 2021) NIST Recommends Steps to Boost Resilience of U.S. Timekeeping - NIST News:
Blog Editor's Note: Good to see NIST weighing in on this issue.
The high level recommendation that the nation needs a coherent timing architecture that involves space, terrestrial broadcast, and fiber assets is consistent with numerous other findings and studies, including RNTF white papers.
A few notes:
This paper only discusses/ recommends things for which NIST is already funded. To do otherwise would be to talk about funding and program needs that had
not been approved. This would likely bring down the wrath of the Office of
Management and Budget (OMB). Thus, for example, better use of existing 60KHz
at that NIST time signals is recommended despite 100KHz being more of an international standard and the science and engineering for precise time
transfer frequency being far more developed.
There is discussion of Two Way Satellite Time Transfer i(TWSTT), but none of Two
Way Low Frequency Time Transfer (TWLFTT). This terrestrial alternative
could be employed with improvements to NIST's existing LF radio systems, and should be an important part of a national architecture robust enough to weather
disturbances in space.
The paper also errs saying eLoran depends on GNSS. That has never been the case.
Multiple nations have adopted eLoran as a terrestrial time signal
specifically because it is entirely INDEPENDENT of GNSS.
We also have to comment about the statement in the NIST post below that "A previous NIST-sponsored report estimated that the combined loss of GPS
position, navigation and timing services would cost the U.S. economy at least $1 billion per day." That does seem like a lot, until you run the numbers and
realize that is less than a 2% reduction in GDP. We think GPS is WAY more important than that.
This report was issued at the same time as another that explored dependence on GPS time in stock markets, electrical grids, and telecommunications networks.
One statement in this second paper particularly stands out:
“The impact of a long lasting, widespread GPS outage on mobile phone networks would likely be staggering.”
The paper does not define "long lasting," but we are reliably informed it means "24 hours or more."
Links to both papers are included in the NIST post below.
NIST Recommends Steps to Boost Resilience of U.S. Timekeeping
November 29, 2021
NIST staff use this equipment to compare time signals transported over fiber-optic cable, a new way to distribute highly accurate NIST time standards. When
the large spool of test fiber (330 meters) is inserted into the link between two points, there are negligible changes in delay and stability, indicating
that time signals remain virtually unaffected by distance. Signals travel in both directions through the single strand of fiber so that round-trip and
one-way delays can be compared. (Commercial brand names were deleted from the photo.)
The nation should bolster research and development of systems that distribute accurate time via fiber-optic cable and radio as part of the effort to back
up GPS and enhance the resilience of critical infrastructure that depends on it, according to a new report by the
National Institute of Standards and
Technology (NIST).
Many aspects of the U.S. economy and quality of life depend on accurate time, as detailed in a second, companion report. Time is a crucial underpinning of
telecommunications networks, for example, as well as the power grid and stock markets, among other users.
The two reports are part of NIST’s response to the Feb. 12, 2020, Executive Order 13905,
Strengthening National Resilience Through Responsible Use of
Positioning, Navigation, and Timing Services.
The work was funded in part by the U.S. Department of Homeland Security, which commissioned NIST to “study and assess the ways in which
Coordinated Universal Time (UTC) can be distributed to the public and private sector,” adding that the “performance of this distributed time should be precise
enough to meet the requirements of critical infrastructure users.”
An overarching concern is the need for alternatives to GPS and other global
navigation satellite system (GNSS) timing signals, which are vulnerable to
both accidental and deliberate interference. A previous NIST-sponsored report estimated that the combined loss of GPS position, navigation and timing
services would cost the U.S. economy at least $1 billion per day.
As longtime keepers of the U.S. civilian time standard, NIST staff members envision a resilient architecture for generating and distributing NIST’s
version of Coordinated Universal Time as combining existing, emerging and proposed systems. The full development of a resilient architecture will
require commitments by NIST, industrial partners, and other private and
public organizations, the report notes.
“We are working hard to find new ways to support critical infrastructure systems with non-GNSS timing references to fulfill the Executive Order,” said
Michael Lombardi, leader of NIST’s Time Realization and Distribution Group. “This is a continuous, multifaceted effort that involves our entire group.
It focuses on improving the way that we realize time by strengthening the UTC(NIST) time scale to make it more robust. At the same time we are working
to enhance our existing services and to develop new higher-accuracy services to distribute
UTC(NIST) via optical fibers and via geostationary satellites.”
Recommendations include the following:
Enhance the primary NIST time scale — an ensemble of atomic clocks —
in Boulder, Colorado, and the secondary NIST time scales in Fort
Collins,
Colorado, and Gaithersburg, Maryland, by, for example, increasing the number of clocks and improving their performance and distribution capabilities.
Explore additional uses of two-way satellite time and frequency transfer, which synchronizes clocks with high accuracy,
using NIST’s new satellite service
and perhaps conducting additional research to reduce the cost of ground stations and expand deployment.
Conduct additional research on time distribution over optical fiber to determine the best way to integrate it into commercial networks, focusing on the
capability to scale up to reach enough users to meet critical infrastructure needs.
Encourage manufacturers to develop clocks that have the ability to automatically switch between multiple reference time scales, multiple signal sources,
and multiple sources of network corrections, in order to achieve true fail-safe redundancy.
Modernize NIST radio station WWVB, strengthen its long-term reliability, and encourage manufacturers of
GNSS clocks to use the stable signal of WWVB as a
frequency source.
Improve the ability of GPS-dependent clocks to keep working during GPS outages and to detect and reject spoofed signals by modifying these clocks to accept
NIST time codes broadcast via radio stations WWVB, WWV and WWVH or the
Internet Time Service.
Consider distributing NIST time through indirect sources, both public and private, such as the Satellite Time and Location service, which uses Iridium
satellites, and resumption of discontinued eLoran radio navigation services.
Report: J.A. Sherman, L. Arissian, R.C. Brown, M.J. Deutch, E.A. Donley, V. Gerginov, J. Levine, G.K. Nelson, A.N. Novick, B.R. Patla, T.E. Parker, B.K.
Stuhl, D.D. Sutton, J. Yao, W.C. Yates, V. Zhang and M.A. Lombardi. A Resilient Architecture for the Realization and Distribution of Coordinated Universal
Time to Critical Infrastructure Systems in the United States. NIST Technical Note 2187. November 2021.
Report: M.A. Lombardi. An Evaluation of Dependencies of Critical Infrastructure Timing Systems on the
Global Positioning System (GPS). NIST Technical
Note 2189. November 2021.
https://www.nist.gov/news-events/news/2021/11/nist-recommends-steps-boost-resilience-us-timekeeping
(December 2021) Following Russia threat, Locata and Ursanav partner for resilient PNT - GPS World:
Blog Editor's Note: We are seeing more and more consolidations and partnerships within the PNT community.
We have also seen larger companies that formerly did not have a strong PNT presence acquiring, or perhaps "absorbing" would be a better word, smaller
firms that focus on PNT equipment and/or services. Orolia's acquisition by Safan is the latest example.
This undoubtedly reflects growing awareness of the criticality of PNT services, recognition that current services are not sufficient for the long term
because of vulnerability and other concerns, and an expectation that there will be customers for new services.
Certainly, as this article points out, Russia is doing its best to help the United States and the West understand all these things.
Full disclosure, UrsaNav, Locata, and Orolia are commercial supporters of the RNT Foundation.
Following Russia threat, Locata and Ursanav partner for resilient PNT:
December 8, 2021 - By Tracy Cozzens
Russia’s recent threat that it could blow up all the GPS satellites with its new anti-satellite technology
(ASAT) should come as no shock to those
following space-related events. In the past, China shot down one of its own low-Earth-orbit
satellites (LEOS) using a medium-range ballistic missile,
and the United States used a modified antiballistic missile to shoot down one of its own spy satellites.
Blowing up satellites, solar flares, ever-increasing hazards from “space junk” and thousands of new satellites in the launch queue all make space a
congested and increasingly dangerous place.
Locata Corporation and Ursa Navigation Solutions Inc. (UrsaNav) have announced a technology partnership specifically
aimed at providing resilient PNT
(positioning, navigation and timing) solutions to national governmental and commercial interests globally.
Combining Locata’s high-accuracy local-area
and UrsaNav’s very wide-area PNT produces a potent solution that lessens any nations’ dependency on easily disrupted and increasingly vulnerable
space-based signals.
Locata has for many years been delivering proven centimeter-level positioning and picosecond-level timing to demanding users including the
U.S. Air Force,
NASA and globally significant commercial partners. Professional users in demanding industries such as ports, mining, the military, aviation, automotive,
logistics, indoor positioning and high-accuracy timing depend on Locata systems every day.
UrsaNav’s eLoran and LFPhoenix technologies provide nanosecond-level timing, meter-level positioning, and short-message-service-like data transmissions at
distances often exceeding 1,000 miles over land and 1,800 miles over water. Its two-way
low-frequency time and frequency transfer (TWLFTFT) service is
embedded in the PNT signal, providing a wireless timing synchronization conduit between any set of transmission sites.
READ MORE: https://www.gpsworld.com/following-russia-threat-locata-and-ursanav-partner-for-resilient-pnt/
(December 2021) u-blox's upgraded ZED-F9P high-precision #GNSS receiver module achieves reliable centimeter-level accuracies in seconds. #positioning
https://bit.ly/3rI9dS6
https://www.gpsworld.com/u-blox-upgrades-gnss-receivers-for-faster-cm-accuracy/
(December 2021) Some more sad news in the radar community with the passing of Prof (Emeritus) Donald Weiner of Syracuse University.
He had a profound impact on many young engineers who went on to great careers in radar!
https://lnkd.in/gKHPjpZq
(December 2021) Congress wants Hawaiian missile defense radar up and running by end of 2028:
https://trib.al/jM68Nlt
(December 2021) Some more sad news in the radar community with the passing of Prof (Emeritus) Donald Weiner of Syracuse University.
He had a profound impact on many young engineers who went on to great careers in radar!
https://lnkd.in/gKHPjpZq
(December 2021) Success in Visualizing the Propagation Path of Electromagnetic Waves from Space to Ground:
Using data on electromagnetic (EM) waves and plasma particles measured simultaneously via multiple satellites, an international collaborative research
group has discovered the existence of invisible “propagation path” of EM waves and elucidated the mechanism by which
EM waves propagate to the ground.
https://www.kanazawa-u.ac.jp/latest-research/99573
(December 2021) Swarm Talk: Understanding Drone Typology - Modern War Institute:
Drones within a drone swarm should be categorized based on the roles they play within the swarm. I argue in Modern War Institute at West Point that five
categories exist: attack (and other effects), sensors, communication,
decoys, and mothership drones.
Militaries should experiment with different combinations of drones to determine which are most effective in various circumstances. This may require
modeling
and simulation, exercises, and war gaming in real and synthetic
environments.
https://mwi.usma.edu/swarm-talk-understanding-drone-typology/
(December 2021) Twenty Years On, SABER instrument on TIMED spacecraft Still Observing the Upper Atmosphere:
So much of the well-known science on Earth's atmosphere focuses on what's happening in its lowest two layers — the troposphere down here where we live and
work, and above that, the stratosphere, home to the ozone layer. But 20 years ago today, scientists watched a satellite lift off that they hoped would give
them a few good years of insight into the workings of two of the highest regions of the atmosphere — the mesosphere and thermosphere. By just about any
measure, the Sounding of the Atmosphere using Broadband Emission
Radiometry (SABER) instrument aboard the Thermosphere, Ionosphere,
Mesosphere, Energetics
and Dynamics (TIMED) spacecraft has exceeded whatever modest expectations scientists had for it two decades ago. A well-built instrument on a well-built
satellite, SABER is still collecting data with no signs of slowing down any time soon.
"SABER has exceeded our wildest expectations by a longshot. In
addition to understanding the basic workings of the mesosphere and lower thermosphere, there have also been many unexpected findings, including
groundbreaking observations of infrared radiation that are being used to develop new techniques to forecast 'space weather,’ which is vital to protecting
space assets such as the International Space Station," said Marty Mlynczak, SABER principal investigator at NASA's Langley Research Center in Hampton,
Virginia. "Graduate students who did their doctoral work using SABER data are now university professors up for tenure.
TIMED and SABER have truly touched
the future as only NASA can." My Comment: Hey, DoD can touch the
future too (and destroy it all)!
(December 2021) From downed drones to stolen quad bikes: a review of GNSS vulnerabilities in 2021 - Guy Buesnel on
Linkedin:Blog Editor's Note: We love these 'year end reviews' Guy publishes. He and his LinkedIn group are great sources for information on jamming, spoofing, and
interference of all kinds.
While we try to keep close track of these kinds of things ourselves, Guy always has some interesting cases that we had not seen before.
We are very glad to have Guy as a member of RNTF's International Advisory Committee (full disclosure,
Guy is employed by Spirent, a corporate supporter of
RNTF).
Well done, Guy!
From downed drones to stolen quad bikes: a review of GNSS vulnerabilities in 2021
Published on December 14, 2021
Guy Buesnel
PNT Security Technologist - with expertise in testing system robustness against GPS Interference and spoofing threats
As GPS jamming becomes endemic in some parts of the world, 2021 saw a big step towards resilient PNT standards for
safety- and liability-critical systems.
Users of satellite-based position, navigation and timing (PNT) systems have for a long time been engaged in an arms race with a variety of threats that
prevent those systems from operating.
In 2021, some of those threats have become endemic – at least in certain parts of the world. From the
Arctic Circle to the Suez Canal, and from China to
the USA, jamming of global navigation satellite systems
(GNSS) made life very difficult this year for users of PNT systems, particularly in commercial
aviation and maritime operations.
Signal jamming continues to increase in geopolitical hotspots
In September, for example, Defence and Security Systems International reported that
“the volume of GPS jamming incidents has increased across the globe”.
In particular, it noted that “in the Middle East, jamming incidents of both civil and military platforms are equally common” and that “there is extremely
aggressive Electronic Warfare in the area of Ukraine and in the Baltic region.”
Indeed, in May, the United Nations OSCE Special Monitoring
Mission (SMM) to Ukraine reported that one of its observation drones was forced to make an
emergency landing after GPS jamming disabled its onboard navigation systems, preventing it from carrying out its
mission.
Vessels find DIY workarounds in the Eastern Mediterranean
Also in September, the US DoT Maritime Administration extended its maritime industry
advisory (MARAD) for the Eastern Mediterranean – a vast region
encompassing Italy, Cyprus, Egypt, Lebanon and other countries. It warned commercial shipping operators of continued “instances of significant interference…
resulting in lost or inaccurate GPS signals affecting bridge navigation, GPS-based
timing, and communications equipment.” Most of this activity is likely
related to ongoing conflict in Syria.
Reports from individual vessels published on the US Coastguard’s Navigation Center
(NAVCEN) database show what this interference looks like operationally.
Two separate ships’ captains reported that GPS jamming around Port Said is so bad that they decided to switch from
GPS as their primary position sensor to
a secondary receiver that also uses the Russian GLONASS system. “It worked,” reported one. “We
never received alarms, or lost our ECDIS picture.”
Switching to GLONASS may have worked for these users, but DIY workarounds like this are
not a viable long-term solution to the problem of continual signal
jamming. Instead, commercial GPS users in geopolitically sensitive regions need practical advice on protecting and toughening their
systems, and
augmenting them where possible with additional positioning technologies.
Domestic jamming poses a growing threat to commercial aviation
And signal jamming isn’t just happening in conflict zones. The USA has seen a sharp increase in domestic military jamming
tests, creating problems for
commercial pilots. In May, previously undisclosed FAA data revealed that in 2017 and
2018, hundreds of aircraft lost GPS reception in the vicinity of
military tests.
One report to NASA’s Aviation Security Reporting System
(ASRS) exemplifies the problem. The flight crew had become so used to jamming near a missile range
that when they experienced a course error, they assumed it was due to military
testing. In fact, the crew had introduced the error themselves through
inaccurate data entry. “Expectation bias led me to being complacent about a required descent briefing,” admitted the crew member submitting the report.
In May, the Federal Aviation Authority said it acknowledged the concerns of commercial aviation, but its proposed solutions – such as extending notice
periods of jamming events – were unlikely to help much, according to the Aircraft
Owners and Pilots Association (AOPA).
New resilient PNT standards may provide a solution
In light of the growing threats from jamming interference, it was very encouraging to see major steps being taken this year towards resilient
positioning,
navigation and timing (PNT) standards.
In August, the IEEE started work on developing the P1952 resilience standard for receivers used in critical
applications. Spirent is happy to be a
contributor to this ongoing project, and we would encourage others in the industry to get involved too.
If you’d like to know more, Spirent’s on-demand webinar series and accompanying series of blogs explains why resilience standards are needed for PNT
systems, how to conduct a risk assessment of your PNT system, and how to test its resilience.
What other GNSS vulnerabilities came to light in 2021?
While the threat to shipping and aviation from military jamming was the big theme of the year, we also saw many other incidents and threats. Here’s a quick
roundup of some that stood out:
January: In India’s Telangana province, thieves employ a GPS jammer to defeat tracking devices protecting a shipment of gold. A cunning plan… except it seems
they forget to switch the jammer on, enabling Telangana police to locate the gold – and apprehend the thieves.
March: The Arctic Institute reports on escalating geopolitical tensions in the Arctic
Circle, where climate change is prompting new economic and territorial
interests. Those tensions have already included “several incidents of Russian
jamming, resulting in lost GPS signals for both civilian and
allied air traffic
in the northern part of Norway,” according to the Institute.
May: Farmers Weekly reports that some farmers are experiencing interference issues with John Deere Starfire 3000 and older Starfire 6000 satellite receivers.
John Deere UK and Ireland confirms that a small number of customers in the UK and the
Netherlands have been affected, and says the interference is caused
by newly-introduced 4G mobile network frequencies.
June: A drone display goes badly wrong in Shanghai when “dozens of drones” start falling from the sky in a waterfront area of the
city. No explanation is
given, but in October, a similar incident occurs in Zhenghzhou. There, local drone technology reporter Kanzhaji says organizers suspect their competitors
of transmitting interference to overwhelm the drones’ navigation systems.
With incidents like this becoming more common, drone operators will need to tighten defences against
GPS interference to avoid the risk of personal injury
or property damage.
August: NFU Mutual’s 2021 Rural Crime report reveals that criminals in the UK are using
GPS jammers to assist in the theft of quad bikes and other expensive
farm vehicles equipped with GPS tracking devices.
October: The US Cybersecurity and Infrastructure Security Agency
(CISA) issues a warning about a GPS Daemon (GPSD) bug that may take effect on 24th October,
with possible impacts on critical infrastructure. The bug particularly affects two versions of the
GPSD software, it says.
This has echoes of the 2019 GPS week number rollover event, which affected systems ranging from New York traffic lights to Australian weather balloons.
Although no incidents have been reported (that I know of) from the GPSD bug, it does highlight the importance of understanding how systems rely on
GPS for
timing, and ensuring those systems are adequately protected.
December: In Canada, there are reports of criminals using GPS and Bluetooth trackers to track target vehicles with a view to
eventually stealing them. If
this trend continues, it may encourage otherwise law-abiding citizens to consider employing a GPS jammer to prevent
tracking.
My prediction for 2022: More focus on location authentication
Given all that’s happened in 2021, how is GNSS cybersecurity likely to evolve in 2022? Apart from the development of resilience standards, my big prediction
is that we’ll see more focus on technology for positioning authentication and proof of location.
Such technologies will be needed to combat location-spoofing activities like illegal fishing and sand theft. And as companies strive to reduce their
environmental impact, they’ll also be needed to provide reliable data on supply chain routes taken and carbon emitted.
Authentication schemes like Open Service Navigation Message
Authentication (OSNMA) for Galileo and CHIMERA for
GPS are already advanced, and we should
see early adopters starting to use them in the coming year. Ultimately, I expect authenticated position and trajectory history will become core business
components across many relevant sectors.
Stay up to date with GNSS vulnerabilities
Threats to GPS/GNSS are evolving all the time. To stay up to date with the latest news, events and incidents, join nearly 2,000 industry professionals in
the GNSS Vulnerabilities LinkedIn group.
LINK TO ORIGINAL POST: https://www.linkedin.com/pulse/from-downed-drones-stolen-quad-bikes-review-gnss-2021-guy-buesnel/
(December 2021) Core mate complete for final GPS III satellite, IIIFs to follow - GPS World:
https://www.gpsworld.com/core-mate-complete-for-final-gps-iii-satellite-iiifs-to-follow/
(December 2021) Video: National Resilient Timing Architecture @ PNT Advisory Board:
RNT Foundation Dana A. Goward spoke to 25th meeting of the President's National Space-based Positioning, Navigation, and Timing Advisory Board last week.
Citing cases like Hurricane Katrina and the 9/11 attacks, his thesis was that, despite knowing about a problem and what needs to be done, America often
has a hard time acting to prevent foreseeable disasters.
If you are having trouble with the above direct link, the presentation begins at 6:08:00 on the conference video available at the Advisory Board's website.
https://www.youtube.com/watch?v=LqxHHlesxFQ
(December 2021) Bei Dou & China's Rise - GPS & America's Decline?:
Blog Editor's Note: The below article got us thinking again about how a global
navigation satellite system (GNSS) is an instrument of national influence
and power.
In addition to being a very useful tool for a nation's civil and military use, it is a status symbol. It literally shows the nation has captured the high
ground and its economic and technological prowess.
A GNSS' practical uses can also garner allies and make them dependent upon the system's owner.
China is doing an outstanding job with this as shown in the below article. They are also providing free
Bei Dou receivers to the military and civil forces
of neighboring governments, and are undoubtedly suggesting that, since GPS is jammed and spoofed so
often, Bei Dou is a much better way to go. All part of
their larger Belt and Road initiative.
At the same time the US government appears to see GPS as a military system and
apparently has no desire to improve its utility for civil users. Hence it
has fallen behind other GNSS in many ways (see, for example, our 12 December 2021 post).
Bei Dou is clearly an indication of China's ascension in the world.
Is GPS an indicator of America's decline?
China, Arab states to expand BeiDou cooperation
December 9, 2021
By Tracy Cozzens
China and the Arab states will expand their cooperation in using the China-developed
BeiDou Navigation Satellite System (BDS), according to the third
China-Arab States BDS Cooperation Forum and reported by XinhuaNet.
China and the Arab states will jointly implement pilot projects in key domains in the application of
BDS and GNSS over the 2022-2023 period, according
to a cooperation action plan signed at the forum, held Dec. 8 in Beijing.
Both sides will facilitate the establishment of BDS/GNSS centers in the Arab
states, hold training courses on satellite navigation technologies, and
exchange visiting scholars. Each year, China will offer scholarships to three to five students majoring in navigation and communications from the Arab
states, said the action plan.
READ MORE: https://www.gpsworld.com/china-arab-states-to-expand-beidou-cooperation/
(December 2021) New SpaceX Program Converts Atmospheric CO2 Into Rocket Fuel:
https://cleantechnica.com/2021/12/14/new-spacex-program-will-focus-on-converting-atmospheric-co2-into-rocket-fuel/
(December 2021) Cracks could cause key ice shelf holding back "Doomsday Glacier" to collapse:
Scientists have detected new cracks in the key ice shelf that buttresses Antarctica's Thwaites
Glacier, indicating that the ice shelf could break apart
within the next five years.
Why it matters: The destruction of the ice shelf could accelerate the movement of inland ice into the sea, eventually causing sea levels to rise by several
feet and endangering coastal communities worldwide, per the Washington Post.
State of play: The Thwaites Glacier is known as the "doomsday glacier," due to the possibility that it may already be past a tipping point into a virtually
unstoppable, runaway melt.
(December 2021) New SpaceX Program Converts Atmospheric CO2 Into Rocket Fuel:
https://cleantechnica.com/2021/12/14/new-spacex-program-will-focus-on-converting-atmospheric-co2-into-rocket-fuel/
(December 2021) Cracks could cause key ice shelf holding back "Doomsday Glacier" to collapse:
Scientists have detected new cracks in the key ice shelf that buttresses Antarctica's Thwaites
Glacier, indicating that the ice shelf could break apart
within the next five years.
Why it matters: The destruction of the ice shelf could accelerate the movement of inland ice into the sea, eventually causing sea levels to rise by several
feet and endangering coastal communities worldwide, per the Washington Post.
State of play: The Thwaites Glacier is known as the "doomsday glacier," due to the possibility that it may already be past a tipping point into a virtually
unstoppable, runaway melt.
Roughly the size of Florida, the Thwaites Glacier's meltwater already contributes to about 4% of global sea level rise.
The Thwaites Eastern Ice Shelf acts as a brace preventing faster flow of meltwater from the glacier, and the shelf is held in place by an underwater
mountain, according to the Cooperative Institute for Research in Environmental Sciences at the University of Colorado, Boulder.
This part of the ice shelf was previously thought to be stable until scientists took new measurements during a field campaign over the past two years.
Warming ocean water is melting the ice from below, meaning the shelf is gradually losing its grip on the underwater mountain and satellite imagery has
revealed fractures in the shelf.
"Similar to a growing crack in the windshield of a car, a slowly growing crack means the windshield is weak and a small bump to the car might cause the
windshield to suddenly break apart into hundreds of panes of glass," reads a summary of the findings.
The breaking of the ice shelf will increase the flow of ice off Antarctica, it adds.
The big picture: The Thwaites Glacier is situated in a deep basin, so if it collapses, neighboring glaciers would follow, and over the next few centuries
it could lead to the loss of the entire West Antarctic Ice Sheet, contributing to a large rise in sea levels, according to
Science.
“That would be a global change,” Robert DeConto, a glaciologist at the University of Massachusetts, Amherst, told Science. “Our coastlines will look
different from space.”
(December 2021) Extremely pleased that after literally three years of stony silence from the authorities on a new and stealthy naval craft that Janes
#first broke cover on in December 2018:
(subscriber link -- https://lnkd.in/gkt-3DyS), it has finally been officially unveiled!
(December 2021) Core mate complete for final GPS III satellite, IIIFs to follow - GPS World:
The 10th #GPS III space vehicle under the original contract has completed a production milestone known as “core mate” — and received a famous name.
https://www.gpsworld.com/core-mate-complete-for-final-gps-iii-satellite-iiifs-to-follow/
(December 2021) How engineers test hypersonic Weapons and vehicles:
Flying faster than Mach 5 is an old idea. During the 1950s and 1960s US hypersonic flight research programs such as the X-15 rocket plane were the first
to test the concept. Intercontinental Ballistic Missiles, which re-enter the atmosphere at hypersonic speeds were also developed around the same time.
During the decades since then several hypersonic vehicles have been developed for research, then shelved by engineers. But
in the last five years there
has been a resurgence in interest in flying faster than 3,000mph (4,800km/h) primarily in the
USA, Russia, and China.
https://www.aerospacetestinginternational.com/features/testing-hypersonic-weapons-and-vehicles.html
(December 2021) Companies demo robust nav solution for UAVs under GNSS jamming - GPS World:
infiniDome, Honeywell, and Easy Aerial Inc. have successfully demonstrated their new
Robust Navigation System for #UAVs.
https://lnkd.in/gJyePXeS
https://www.gpsworld.com/companies-demo-robust-nav-solution-for-uavs-under-gnss-jamming/
(December 2021) GPS Jammer on Amazon only $14.98! Great Stocking Stuffer!:
One of our members spied this for sale. What a great, useful, and inexpensive gift for the holidays!
And we are glad to see that it is "Made of environmentally friendly materials."
We are not sure about the "will not cause harm to people" statement, though. Traffic accidents because near by vehicles lose
GPS and drivers are even more
distracted? Delays to first responders? Etc.?
Yeah, not so sure it's harmless unless you go for the "Jammers don't hurt people, people hurt people," approach.
Does anyone at Amazon pay attention to this stuff?
We are going to drop a line to the enforcement folks at FCC. Hope they can do something.
(December 2021) Telit has launched the LE910S1-ELG, a new LTE Cat 1 module for #IoT applications in Latin America that need affordability, voice support
and #2G fallback:
https://www.gpsworld.com/telit-launches-gnss-module-with-2g-fallback-for-latin-america/
(December 2021) Was a flying killer robot used in Libya? Quite possibly
By Zachary Kallenborn | May 20, 2021
https://thebulletin.org/2021/05/was-a-flying-killer-robot-used-in-libya-quite-possibly/
(December 2021) 5G: Bringing precise positioning to the connected intelligent edge - Market Screener:
Blog Editor's Note: This item about Qualcomm is part of the recent buzz about the
possibilities of using 5G for location services. Lots of potential
there, we are sure.
Yet our telecommunications system has a critical dependency on GPS-derived
timing. NIST recently called the impact on mobile networks of a extended
loss of GPS (we understand that to mean 24 hours) "staggering."
Last year we proposed a Resilient National Timing Architecture that would go a long way to solve that vulnerability.
In February of this year, a pair of Qualcomm engineers published a paper showing how
eLoran, a leading candidate technology for a national timing
architecture, would be a good fit for supporting 5G..
We can't continue to ignore our tech infrastructure by not having
a reliable timing base. Otherwise we continue to build houses of
cards.
5G: Bringing precise positioning to the connected intelligent edge:
When we think of locating ourselves in the world or navigating to our destinations, satellite-based technologies like the
global positioning system (GPS)
readily come to mind. With a constellation of satellites covering the globe to help users resolve their location,
GPS was a major improvement over earlier
positioning technologies including closest cell tower and OmniTRACS for fleet
management. We now have multiple satellite constellations to complement GPS.
Smartphones and other compact positioning devices can use a combination of
global navigation satellite systems (GNSS) like
GPS, GLONASS, Beidou, and Galileo,
and regional navigation satellite systems (RNSS) like
QZSS and NavIC to provide meter-level precision.
Precise positioning benefits a broad range of use cases and devices
READ MORE: https://www.marketscreener.com/quote/stock/QUALCOMM-INC-4897/news/5G-Bringing-precise-positioning-to-the-connected-intelligent-edge-37362136/
(December 2021) "The impact of a long lasting, widespread GPS outage on mobile phone networks would likely be staggering..." -
NIST:
Yet another government report detailing bad things that will happen because of our foolish over reliance on GPS for
timing.
We understand, by the way, that in the terms of this report a "long lasting" GPS outage would be "24 hours."
Government and industry reports about these kinds of problems have been around for twenty years.
The 2001 Volpe Center report forecast all the problems we
are seeing now, including Russia trying to hold the US hostage with threats to shoot down GPS.
We are sometimes reminded of the movie "Cool Hand Luke." In it, the prison camp boss, played by Strother Martin, tells a wise guy prisoner, played by Paul
Newman, "What we have here, is failure to communicate."
Communication requires two parties, though, a sender and a receiver. In this case,
the engineers and technologists have been sending for twenty years, BUT
corporate and government leaders have not been receiving.
What's it gonna take to get them to listen?
An Evaluation of Dependencies of Critical Infrastructure Timing Systems on the
Global Positioning System (GPS)
Starting on page 48:
The impact of a long lasting, widespread GPS outage on mobile phone networks would likely be staggering, due to the large number of
GPSDCs in use. The
number of GPSDCs employed in U. S. mobile phone networks already
numbers in the hundreds of thousands and may increase dramatically as 5G coverage
improves. Mobile phone providers install their BTS equipment at shared cellular sites that are typically located on towers or rooftop platforms, but
they do not share equipment. Therefore, a quick glance at any cellular site usually reveals multiple GPS
antennas, which either indicates multiple
providers or multiple systems operated by the same provider that each require
synchronization. CTIA, a trade association that represents the wireless
communications industry in the U. S., estimates that 349,344 cell sites were operational in 2018 [125]. Following the plausible assumption that on
average at least one, and not more than three GPSDCs are located at each
site, results in an estimate of 350,000 to 1 million devices now in service.
A widespread rollout of 5G sites is now underway to meet the strong demand for faster data transfer. The
5G rollout involves “small cell” or “micro
sites” that cover a limited geographic area and more sites will be needed to provide the necessary
coverage. Some analysts predict that the number of
cellular sites will triple or quadruple within a few years [126, 127], with perhaps a corresponding increase in the number of
GPSDCs.
LINK TO REPORT: chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/viewer.html?pdfurl=https%3A%2F%2Fnvlpubs.nist.gov%2Fnistpubs%2FTechnicalNotes%2FNIST.TN.2189.pdf&clen=5497385&chunk=true
Grant Taylor Comment:
Navigation and Broadcast systems
"5G rollout involves “small cell” or “micro sites” that cover a limited geographic
area", you could add here the operating cost of all those extra smaller
sites will lead to higher phone prices. As you go up in frequency the base station amplifier come less
efficient, as I have done a lot of research in
amplifier design over the last four years.
Getting back to GPS timing, this should be used along side other forms
of timing such fiber optic and radio broadcast services as they operate of wide cover
areas. There has been a large push to synchronize the carriers of broadcast
transmitters, but there has been no funding provided to do this, it would
not
take much to encode a full PNT service without using GPS.
(December 2021) Threats to GPS - 2021 Year in Review, GPS World Special:
Blog Editor's Note: We subscribe to GPS World's "Navigate!" weekly newsletter." You should too.
This week's newsletter was a 2021 Year in Review and led off with a section on "Threats to GPS."
Russia Issues Threat to GPS Satellites
The Kremlin warned it could blow up 32 GPS satellites with its new anti-satellite
technology, ASAT, which it tested Nov. 15 on a retired Soviet Tselina-D
satellite, according to numerous news reports.
READ MORE: https://www.gpsworld.com/russia-issues-threat-to-gps-satellites/?utm_source=Navigate%21+Weekly+GNSS+News&utm_medium=Newsletter&utm_campaign=NCMCD211222002&oly_enc_id=9675F1206356D9T
(January 2022) GNSS Jamming: An Omnipresent Threat - GW Prime:
Blog Editor's Note: An interesting overview article that also includes some tech details and several case studies. We especially like case studies as they
are a good way to make what "might happen" real. We note that folks who jam and spoof usually take pains to avoid detection. Thus, whenever these cases
make it into the press we are seeing both the tip of the iceberg and a glimpse of more widespread current and future activity.
The article concludes with some information on how to make receivers more robust and resistant to jamming and spoofing. It's actually a bit of an ad for
one of our corporate members. they are a good company and we strongly agree these measures can be helpful and should be used where and whenever possible
and affordable.
We also think that establishing a terrestrial wireless source of PNT that could be easily accessed would (1) deter a lot of jamming and spoofing as it
would have less impact on serious PNT users, and (2) provide users an alternative to relying entirely on weak space-based signals that could be disrupted
from any number of accidental, natural, or malicious sources. Some nations (e.g. China, Russia, South Korea, among others) have already done that. Most
have announced the reason for doing so as avoiding space as a single point of failure.
In the U.S. there is a law that requires such a system. Unfortunately the last administration ignored it and the current one has yet to act.
We hope the current administration's policy is not "Sit tight and assess."
GNSS Jamming: An Omnipresent Threat
The deployment of jammers that are easily available on e-commerce websites, military conflicts, faulty wireless equipment, or poorly designed radio frequency
transmitters can disrupt or jam GNSS/GPS signals. Whatever be the cause, the consequences of jammed GNSS signals can be far-reaching.
By Vivek Mukherji & Lt. Gen. (Dr.) AKS Chandele
The use of Global Navigation Satellite Systems (GNSS) has become ubiquitous in our lives. Today, there is hardly any human or economic activity in which
one of the satellite systems, such as, the GPS (USA), GLONASS (Russia),
Galileo (Europe), and BeiDou (China) is not used. Besides, countries like India
are also launching their own systems like the Indian Region Navigation Satellite System
(NaVIC).
With ever-increasing reliance on GNSS in every walk of life for position,
navigation, and timing (PNT), within the framework of location the need for
bulletproofing these systems from intentional and unintentional disruptions (jamming and spoofing) is even greater than before. Of all the satellite
navigation systems, GPS (Global Positioning System) is most widely used around the world.
Since GNSS signals travel a long way from geostationary satellite constellations, orbiting at approximately 22,000 miles (35,000 km) above the Earth’s
equator, they become weak by the time they reach the earth stations/receivers and are susceptible to interference. Typically,
GPS signals operate in
three radio frequency (RF) bands: L1 (1575.42 MHz), L2 (1227.6 MHz), and
L5 (1176.45 MHz). Due to the weak nature of the signals, any form of RF
interference can cause severe disruptions to position, velocity, timing, and navigation, which are critical in virtually every industry and sector. Any
disruption can lead to partial or full jamming of GNSS/GPS receivers and potentially cause serious harm and economic losses.
READ MORE: https://www.gwprime.geospatialworld.net/special-feature/gnss-jamming-an-omnipresent-threat/
(January 2022) NSC director: GPS ‘Still a Single Point of Failure’ - GPS World:
January 4, 2022 - By Dana Goward
The Global Positioning System (GPS) is “still a significant single point of failure in our country,” said Caitlin Durkovich, National Security Council
director for Resilience and Response.
Her remarks were made at the Dec. 9 meeting of the president’s National Space-based Positioning, Navigation and Timing (PNT) Advisory Board.
The meeting was held shortly after Russia’s successful anti-satellite test and threat to “blind NATO and the U.S.” by shooting down all GPS satellites.
Durkovich’s remarks were made in the context of a larger national resilience message. She cited recent incidents such as Hurricane Ida, the Colonial Pipeline
hack, the winter failure of the Texas electrical grid, and disrupted supply chains. She said everyone is responsible to ensure they, their systems and the
nation are able to safely weather adverse events and bounce back better than before.
The interconnectedness of so many vital services such as electrical power and other vital systems like PNT make a holistic approach necessary. The
administration is developing a set of resilience principles to support that, she said. It is also ensuring as funds go out to states and localities
from the infrastructure bill that making American infrastructure more resilient to climate change and “all hazards” is a priority.
Because “positioning, navigation and timing is foundational to our life,” she said, “resilience is more important now than ever.” Disruptions could
lead to “cascading effects.”
Durkovich cited the administration’s Space Priorities Framework as evidence of White House concern. Released this month, it says in part:
“Space systems are an essential component of U.S. critical infrastructure — by directly providing important services and by enabling other critical
infrastructure sectors and industries. The United States will enhance the security and resilience of space systems that provide or support U.S. critical
infrastructure from malicious activities and natural hazards.”
She also indicated that the Biden administration was following through on two Trump administration policies as important steps to resilience.
Executive Order 13905, “Strengthening National Resilience Through Responsible Use of Positioning, Navigation, and Timing Services,” among other things,
calls on all users to avoid over-reliance on GPS. It also calls for the federal government to require PNT resilience to be considered when selecting
contractors.
Space Policy Directive 7 “The United States Space-Based Positioning, Navigation, and Timing Policy” outlines a number of research and other efforts. It
also says the nation will:
“Invest in domestic capabilities and support international activities to detect, mitigate, and increase resilience to harmful disruption or manipulation
of GPS, and identify and implement, as appropriate, alternative sources of PNT for critical infrastructure, key resources, and mission-essential functions.”
Several board members asked about the Federal Communications Commission’s (FCC) order authorizing Ligado Networks to broadcast in frequencies adjacent to
those used by GPS. She said the administration was concerned and both the National Economic Council and National Security Council were in discussion.
Engagement with the FCC, though, may pend confirmation of a full board of commissioners.
One of the board members asking about the Ligado issue followed up with a comment that adjacent-band concerns pale in comparison to recent Russian threats
to GPS satellites. Durkovich responded that there wasn’t much she could say on that topic in public except that it had the attention of the president and
his senior advisors.
Durkovich was also asked about the administration’s commitment to execute the 2018 National Timing Resilience and Security Act. The law’s requirement to
establish a terrestrial, wireless source of coordinated universal time to back up GPS signals by December 2020 was ignored by the Trump administration.
Her reply was to reaffirm her earlier statement that “assuring positioning, navigation and timing, and the economic and strategic benefits it brings to
this nation, is a priority for this administration.”
Video of the entire advisory board meeting is available on YouTube. MS Durkovich’s remarks begin at approximately 1:37:00. A link to the video is also
posted as part of the agenda on the board’s website.
READ IN GPS WORLD: https://www.gpsworld.com/nsc-director-gps-still-a-single-point-of-failure/
(January 2022) China Besting U.S. in Nav Warfare, Now Leading World - eLoran Latest Example:
Here is the first sentence in a Chinese research paper on eLoran we saw the other day:
"The eLoran system is an international standardized positioning,
navigation, and timing service system, which can complement global navigation satellite
systems to cope with navigation and timing warfare."
China has been very active developing its eLoran capability over the last few years. This has included making it more precise by adding differential
capability, and expanding coverage to the west so the entire nation has service. The expansion effort was specifically to protect against disruption
of space-based signals from CMEs and hostile action.
At the same time Bei Dou, China's answer to GPS, has many features to serve both military and civilian users that are not found in the American system. A
quick comparison of the two systems shows the result of harmful U.S. budget and leadership policies that try to separate
GPS military and civil utility
and fund them separately. This harmful artifice has directly caused the U.S. to slip into second or third place as a GNSS provider.
It has also made the U.S. highly vulnerable to GNSS disruption by stymying civil agency efforts to comply with the law and establish a terrestrial national
PNT capability.
According to analysts, this invites disruptions to GPS, especially from our adversaries China, Russia, and Iran who have terrestrial systems in place for
use when GPS and other space assets are not available.
It is no surprise then, that threats to GPS continue to grow. China and Russia have both demonstrated the ability to deny or deceive signals over very wide
areas, as well as to directly attack and destroy the satellites. Russia has even explicitly threatened to destroy
GPS satellites, seemingly as part of their
ambitions in Ukraine.
Even if the U.S. is able to avoid overt PNT-related conflict with one or more of its adversaries, this all plays into China's narrative of besting the U.S.
and replacing it as the world's leading power writ large.
China's Comprehensive PNT System - Outlined for 2035, many of the components are in place now.
https://rntfnd.org/2019/11/15/china-leads-world-with-plan-for-comprehensive-pnt-gps-world/
Unlike the U.S.'s backward, stovepiped, and reluctant approach to PNT, China has taken a "comprehensive" approach."
PNT is available from satellites at GEO,
MEO, and LEO, eLoran, and precisely measured fiber networks. Reports indicate that 5G telecom networks will also be used, and research into better
CSAC,
inertial systems and other PNT systems is on-going.
China clearly understands that PNT is essential tech infrastructure that all citizens need to make a nation great.
And it also understands how important PNT is to other nations and its leadership in the world. China is actively promoting Bei Dou's advantages and GPS's
weaknesses, especially with its neighbors in Asia, and frenemies in Africa.
If the U.S. is to even begin addressing this leadership gap, we must have focused
PNT leadership.
The good news is this should be a politically neutral issue. One on which the nation might be able to stop bickering and come together.
The bad news is we see no sign of this. Just a continuation of short sighted and counter-productive budget and bureaucratic rules that erode American
leadership and make it more vulnerable.
https://www.mdpi.com/2072-4292/14/2/250
https://rntfnd.org/2020/11/27/china-research-paper-on-differential-eloran-sensors-journal/
https://rntfnd.org/2020/10/12/china-expanding-loran-as-gnss-backup-gps-world/
https://rntfnd.org/2021/12/16/bei-dou-chinas-rise-gps-americas-decline/
https://rntfnd.org/2021/12/11/gps-unintended-consequences-war-pnt-advisory-board/
https://rntfnd.org/2021/11/30/russia-issues-threat-to-gps-satellites-gps-world/
(January 2022) Clean messy data in seconds with Live Editor tasks: http://spr.ly/6044J7DC4
(January 2022) Regarding the importance of the "vision" aspect: for me, as a kid growing up (in the late 1940's and early to mid-1950's), I would view
the TV program "Disney Land" on TV and would hang on each word of Wernher von Braun, as the featured speaker in 1955 (two years before the 1st man-made
satellite was launched), discussing future plans for man to go to the moon and to eventually inhabit an orbiting Space Station, that would slowly rotate
to create the effect of an artificial gravity (and each goal eventually came to fruition with the proper underlying requisite hard engineering work that
you described as being the necessary stepping-stones to eventually get there)! However, van Braun's "vision" did indeed help point the way for others to
proceed by providing the "Big Picture" early on. This was important technical leadership inspired by previous experience.
(January 2022) James Kiessling, Systems architect and analyst:
To Jim Durling: Its a sample of how such questions should be examined in terms of the limiting physics to scope the needed R&D before you start writing
checks on taxpayers money for a marketing vision. In a similar vein, claims for weapons should be compared with the physical issues before getting excited
there as well. (Note the recent hype on Railguns before they (again) ran into a brick wall of practicality issues and the Navy opted to improve their
powder gun projectiles instead.
Tom Kerr: But didn't some "rail guns" find a useful home on some modern U.S. aircraft carriers by aiding in the efficient launch of fighter aircraft
(e.g., F-35's) from the decks?
James Kiessling, Systems architect and analyst: Not even close to correct sir - EMALS is basically the accelerator section of a modern roller-coaster. A
railgun draws enormous arcs across the projectile eroding both it and the rails.
Tom Kerr: https://migflug.com/jetflights/navy-getting-ready-to-unleash-an-electromagnetic-aircraft-catapult-on-carrier/
I had seen many successful jet launches from Aircraft Carriers on LinkedIn about a year ago. Perhaps the term "rail gun" was inappropriate for me to use
and electromagnetic induction aided launch is more acceptable? Perhaps the link that I cite is dated?
(January 2022) Tom Kerr further comment to James Kiessling: This update discusses some initial problems encountered with EMALS and some resolutions:
https://en.wikipedia.org/wiki/Electromagnetic_Aircraft_Launch_System
regarding MTF's and their resolution and follow-up substantiation. EMALS could
not be backfitted to prior Nimitz-Class Aircraft Carriers, but many other
countries (e.g., France, China, India, UK, Russia) have subsequently signed up to also use this same
EMALS technology for their newly emerging aircraft
carriers, as listed at the bottom of the screen associated with the link included
here just above. Advantages & Criticisms are also explicitly listed.
(January 2022) How is GPS different from its main rival GLONASS?:
https://www.rbth.com/history/334628-gps-glonass-what-difference-navigation
Although the two systems may seem to be competitors, they often complement each other.
GLONASS, the Russian analog of the Global Positioning System
(GPS) created by the U.S., began development in the 1970s as an alternative satellite-based
navigation and positioning system, but it only gained prominence in the 2000s.
Cold War space race
Soviet scientists began exploring the theoretical possibility of using satellites to launch an independent navigation system back in the 1950s, around the time when the Soviet space program successfully launched the first artificial Earth satellite — Sputnik 1 — on October 4, 1957.
This pioneering theoretical work, however, progressed slowly due to a lack of funds. Then the Cold War changed all that.
By the early 1960s, the Soviet leadership learned that the USSR’s archenemy, the U.S., had been working on its satellite-based navigation system since the
1950s and that work had finally produced results. The so-called Transit system developed to track the U.S. ballistic missile submarines, entered U.S. Naval
service in 1964. The Soviet Union of course had to catch up. The same year, the Soviet leadership ordered the restart of the country’s research in the area
of satellite-based navigation.
In 1976, the system dubbed by the Soviets as Cyclone was adopted by the military. It consisted of six spacecraft orbiting near-polar orbits at an altitude
of 1,000 km.
The accuracy of the new Cyclone system had to be drastically improved as the error in properly identifying an object’s location could be up to 80-100 meters,
which is too much by modern military standards.
24 satellites
Since then, both Soviet and later Russian scientists continued to develop the groundwork laid out by the Cyclone creators.
The project regained momentum in 2001 when the Russian government adopted the federal program called "Global Navigation System” and set a roadmap for the
development of the Russian satellite-based navigation system that became known as GLONASS.
This Russian system consists of 24 spacecraft that move in three orbital planes that each have eight devices. In contrast, the American
Global Positioning
System (GPS) uses the same amount of satellites but allocates them in space differently.
GPS’ 24 spacecraft move in six orbital planes, four satellites in
each. The difference in satellite allocation in space affects user experience.
GPS vs GLONASS
Although both systems are highly accurate, GPS slightly surpasses GLONASS both in accuracy and coverage. Used separately, the systems allow for a slight
error in the positioning of the tracked object. In the case of GLONASS, the error might be one or two meters more than in the case of
GPS. To its advantage,
GPS also has global coverage while GLONASS might lose the signal in remote parts of the world.
Yet, GLONASS is superior to GPS when it comes to positioning objects in the North, especially in circumpolar latitudes. Since the Russian satellites do not
resonate with the movement of the Earth (unlike the GPS-based satellites) they do not require auxiliary correction. In practice, it translates into better
reliability of the system in places where Russia needs it the most: in the Arctic where the country’s Northern Fleet operates.
Consequently, while GPS is generally more accurate and widespread, users in northern parts of Scandinavian countries and Russia may find
GLONASS to be more
convenient for them.
Since the Cold War ended the two systems are used as complementary and not as competing. Most tracking devices sold on the market (including iPhones and
smartwatches) allow for simultaneous use of the GPS and GLONASS, drastically increasing the accuracy of the positioning and coverage as a result.
(January 2022) A look back at 2021, a look ahead at 2022 - GPS World:
https://www.gpsworld.com/a-look-back-at-2021-a-look-ahead-at-2022/
(January 2022) The MathWorks "File Exchange Pick of the Week" Discussion:
https://blogs.mathworks.com/pick/2021/12/29/20th-anniversary-most-active-fex-entries/?source=15571&s_eid=psm_15571
(January 2022) Hexagon and Dayou partner to bring high-accuracy GNSS corrections to China - GPS World:
https://www.gpsworld.com/hexagon-and-dayou-partner-to-bring-high-accuracy-gnss-corrections-to-china/
TerraStar X corrections technology enables lane-level accuracy with under one-minute convergence for consumer and automotive-grade
GNSS receivers
Hexagon’s Autonomy & Positioning division has partnered with Chinese positioning company
Dayou to bring TerraStar X technology to the Chinese market.
TerraStar X provides fast precise point positioning
(PPP) corrections for autonomous vehicles and has mass-market use such as in smartphones.
The partnership enables Hexagon and Dayou to provide consistent positioning solutions globally, including North America, Europe and China, so
original
equipment manufacturers (OEMs) can deploy the same design worldwide.
The GNSS corrections generated from TerraStar X technology enable lane-level accuracy with convergence in under a minute for consumer and automotive-grade
GNSS receivers, supporting advanced driver-assistance
systems (ADAS), autonomous applications, safety-critical applications, mobile-phone applications and
more.
(January 2022) Right on time: Protecting critical infrastructure against threats - GPS World:
Blog Editor's Note: Interesting article building upon the idea of a national resilient timing architecture.
We have published two white papers on this idea - "A Resilient National Timing Architecture" in 2020, and "A Resilient National Architecture, Now for
an RFP!" in 2021. In them, we acknowledge the idea that such an architecture will need some monitoring, measurement, and management.
This paper expands upon that a bit.
Full disclosure: The paper's author works for Microchip, an RNT Foundation corporate
supporter.
Right on time: Protecting critical infrastructure against threats:
Managing live sky and terrestrial time sources to protect critical infrastructure against cybersecurity threats
By Greg Wolff, Microchip Technology
Critical public infrastructure systems that rely on GNSS for reception of
positioning, navigation and timing (PNT) data have been identified by national
security agencies across the globe as potential cybersecurity attack vectors. Late in 2020, the U.S.
Department of Homeland Security (DHS) published the
“Resilient PNT Conformance Framework” guidelines, providing a common reference point to help critical infrastructures become more resilient to
PNT attack
threats. Within the framework, a cybersecurity approach has been proposed.
READ MORE: https://www.gpsworld.com/right-on-time-protecting-critical-infrastructure-against-threats/
(January 2022) British Columbia Moves Against Jammers:
Blog Editor's Note: We were glad to get a link to the below article from member Chuck Schue.
It is always good to see law enforcement authorities taking action against jamming devices. We have reported before about police in Scotland, and Hampshire
(UK), doing so. Also about aggressive laws in Mexico against owning and operating jamming devices.
RNTF's mantra for GPS is "Protect the frequencies, Toughen receivers, and Augment signals."
Without the right laws and enforcement capability it is impossible to protect the frequencies.
In the U.S., we are not very far along protecting the frequencies. In fact, the FCC has greatly reduced its ability to detect and act against jamming over
the last couple of decades.
One idea is to empower every state and local law enforcement official to enforce the anti-jamming provisions of the Communications Act. The
detection
equipment they would need is fairly inexpensive, and it could help them uncover other illicit activity.
B.C. expands civil forfeiture to help crack down on crooks' technological tools
With organized criminals making more use of technology such as radio jammers
or GPS trackers, government will adjust civil-forfeiture rules to keep up, said Public Safety Minister and Solicitor General Mike Farnworth:
Author: Derrick Penner
Date: Jan 17, 2022
Radio-jamming devices are easy to get and are increasingly being used by criminals, according to police.
“(They) pose a significant risk to officers during often very high-risk situations, where officers may be conducting interdictions or surveillance of
individuals that pose a significant risk to public and police safety,” said Sgt. Brenda Winpenny, of the B.C. Combined Forces Special Enforcement Unit.
READ MORE: https://vancouversun.com/news/local-news/b-c-expands-civil-forfeiture-to-help-crack-down-on-crooks-technological-tools
(January 2022) How Did the 5G C-Band Threaten to Ground Thousands of Flights? - News:
https://www.allaboutcircuits.com/news/how-did-the-5g-c-band-threaten-to-ground-thousands-of-flights/
(January 2022) 5G & Aviation, France vs U.S.:
US FAA https://www.faa.gov/5g
Blog Editor's Note: This issue is not in the center of our lane. It is a good example, though, of the need for careful leadership and spectrum management
by the FCC. Something that we did not see in their decision on Ligado Networks.
Interesting that the FAA sent information to NTIA before the FCC's decision on
this. But NTIA, overseen by a Commerce Secretary, who supported the telecom
industry at all costs, never forwarded the information to the FCC.
Still, from press and submissions from industry the FCC knew there was an
issue.
If they had been as careful as France's regulators, we would not have this problem today.
(January 2022) DARPA to Develop Robust Optical Clocks to Replace GPS Atomic Clocks:
https://www.defenseworld.net/news/31224/DARPA_to_Develop_Robust_Optical_Clocks_to_Replace_GPS_Atomic_Clocks#.Ye3coOrMI2x
(January 2022) The James Webb Space Telescope Instruments:
https://www.nasa.gov/mission_pages/webb/instruments/index.html
The Integrated Science Instrument Module (ISIM) includes the following instruments: (1) Near-Infrared Camera, or
NIRCam - provided by the University
of Arizona (2) Near-Infrared Spectrograph, or NIRSpec - provided by ESA, with components provided by
NASA/GSFC. (3) Mid-Infrared Instrument, or MIRI
- provided by the European Consortium with the European Space Agency
(ESA), and by the NASA Jet Propulsion Laboratory
(JPL) (4) Fine Guidance Sensor/Near
InfraRed Imager and Slitless Spectrograph , or FGS/NIRISS- provided by the
Canadian Space Agency.
(January 2022)
https://www.flightglobal.com/dod-keeps-eye-on-hypersonic-missiles-and-manoeuvring-warheads/120524.article
(January 2022) The "Ligado Situation" - How did we get here? Where do we go?:
Blog Editor's Note: Last week, RNTF President Dana A. Goward spoke to a study group at the National Academies of Science, Engineering and Medicine. The
study is a congressionally mandated effort looking at the FCC's decision to allow Ligado Networks to broadcast in a frequency band adjacent to that of GPS.
Below is the text of his remarks.
A pdf copy is available HERE and a video of his presentation on 1/20/2022 is available HERE.
Good afternoon.
Eager vacationers were looking forward to their arrival in Sun Valley, Idaho as their aircraft began its approach to the airport nestled in the majestic
Rocky Mountains. At the time, according to the incident report later filed with NASA, there was “an abundance of smoke in the area” limiting visibility.
Air traffic control cleared the airplane to descend to 9,000 feet on a GPS-based instrument approach to the runway. GPS interference had been reported in
the area earlier that day, but, again according to the report, had since cleared up. Minutes after the pilots began their descent, a radar controller 250
miles away noticed the aircraft was descending through 10,700 feet and headed straight for a 10,900 foot mountain. He immediately called the airport control
tower. The aircraft was vectored away from the mountain just in time. The reporting party said, and I quote, “had the Radar Controller not noticed the
problem, the flight crew and the passengers would be dead, I have no doubt.”
You all know that GPS and navigation are important. And you know that the first sign of interference in a GPS receiver is often not complete failure, but
hazardously misleading information.
The interference that caused this aircraft to go off course was undoubtedly accidental. But this case reminds us that signal disruption is not just an
academic concern. It has real life implications and consequences
By way of introduction, I am a lifelong practical navigator. I loved orienteering with the Scouts, served as a navigator of a patrol ship at sea, and spent
years as a Coast Guard helicopter pilot dead reckoning my way at low altitude across trackless waters in the days before satellite navigation. So, I have
long been and still am an avid fan of GPS.
I have also been involved in navigation policy for the last 15 years or so. My last real job was as the maritime navigation authority for the United States
working for the Coast Guard. What I am not is a technologist nor engineer.
So, I am in no position to talk to you about the technical details of your tasking. Even if I wanted to do so, you have already heard from Dr. Brad
Parkinson, the folks at the Department of Transportation and any number of government engineers who are the best in the business. They are much more
technically competent than I could ever be.
I do hope, though, to tell you a few stories as a way of providing context, and also to suggest some things for you to consider in the way of your ultimate
findings and recommendations.
I have several thoughts to share with you in my allotted time and they are inter-related. So, it will be most efficient if we hold off discussion until the
end.
Some of you might be old enough to remember the movie “Cool Hand Luke” with Paul Newman. In the movie, Newman is a prisoner on a southern work gang
and is a real wise guy. He mouths off to the boss, played by Strother Martin, who replies “What we have here is failure to communicate” and then has Newman’s
character severely beaten. “Failure to communicate” is a tag line in the movie and is usually followed by Newman or someone else getting a severe beating.
–What a great metaphor for America today. We are not communicating well with each other at all, and things are going very badly as a result.
On a smaller scale, I am confident “failure to communicate” was a huge problem in the FCC’s decision process on the Ligado application in a couple ways.
First, there were engineers and technologists from completely different backgrounds and orientations looking at the same things and coming to completely
different conclusions.
Dr. Parkinson spoke to you about the significant differences in the ways satellite based radionavigation and radiocommunications use spectrum. That means
folks from these two different technical backgrounds are going to have very different unconscious assumptions, would likely see the same things different
ways, and have a hard time understanding each other, even when they are talking about the same data.
I suspect that in this case the Federal Communications Commission and its communications engineers had a hard time fully understanding radionavigation
experts.
This phenomenon was really brought home to me when I served on an Aviation Week panel with Ligado’s CEO Doug Smith. The topic was, of course, the
impact of Ligado’s proposed transmissions on aircraft operations of all kinds. At one point in the discussion, I said that “Ligado had tested GPS receivers to
the point of failure.” Doug replied that was not true. They had just tested them to the point at which the receivers gave bad information.
A couple issues here. First, bad information is, of course, worse than no information all, in this case. That’s how our pilots trying to land at the Sun
Valley airport almost crashed into the mountain.
And second, it seems to me from Doug’s comment, that he and other communications engineers must understand failure much differently than radionavigation
engineers. Differences in professional backgrounds can also make huge differences in the way public policy makers see issues and can fail to communicate.
Have you ever driven over a bridge and had it strain to hold up your vehicle or even collapse from under you? Probably not.
Now, have you ever heard static on a radio broadcast or had a cell phone call drop? Probably so.
These are the very practical results of the different ways transportation and communications policy makers correctly view their technologies, its uses,
and risks. Transportation folks must limit risk to life and limb. So. they build in lots of buffer between the allowed vehicle weight on a bridge and the
bridge’s point of structural failure, for example.
Communication systems are also important, of course, but the nature of the technology, use, and risk is much different. Broadcasts can usually tolerate
some degradation without failing. And even when communications are lost, a quick do-over is often possible. So, there isn’t as much concern about zero
degradation, or quite so much obsession with systems never failing.
Now at this point, some of you might be saying to yourself, “Well, if GPS and wireless navigation are so critical, why haven’t they been made more resilient
and robust? Where is the concern with no degradation and never-fail?” In this we at the RNT Foundation totally agree. That question is our reason for being.
But that is not your tasking, nor is it why we are here today. Today we are talking about preserving the navigation and timing capabilities Americans have
right now. That means protecting hundreds of millions of GPS receivers that were built to function quite well in an environment established and guaranteed
by the FCC. Protecting them from an environmental change that will harm many.
That’s a bit of context for the first task listed for you on the National Academies web page – deciding which of the two approaches to harmful interference
is more appropriate. In my mind it has to be the more conservative approach supported by the executive branch.
The second item of your tasking is to evaluate the potential harm that might be caused to “DOD operations and activities” by interference from Ligado’s
proposed network.
Thinking about this reminds me of the story of a war game years ago during which, in its last days, commanders were given the chance for “free play.” They
could insert their own problem into the game and see how forces would cope. One creative soul tried to insert the scenario “no more toner cartridges for
printers or copiers.” That was quickly rejected as it would have caused the war game to end almost immediately.
In your deliberations, civil GPS use is the toner cartridge. Forget weapons and other
DOD-only systems for a moment. How would a significant reduction in
GPS effectiveness for all the contractors, suppliers, and employees who use non-military grade systems impact the ability of
DOD to do its job?
Perhaps the problem is only going to be in the homeland. But that is where DOD trains, maintains, and equips. It is where
DOD deploys the nation’s
largest group of first responders, the National Guard. How would all of this be impacted?
For too long in this country we have made a false and harmful distinction between national and homeland security. Between military and civil capability and
strength. It is all one. This is something that China and Russia and our other adversaries know and practice, and it is one of our failings they love to
exploit.
The dividing lines between civil and military GPS use are blurry, if they exist at all. I urge you to take a holistic view of
DOD’s operations and activities
and how critical GPS is to the many essential ways DOD depends upon the civil sector.
Your third tasking item is to evaluate the effectiveness of the mitigation measures in the
FCC order. By the way, the fact that these are included in the
order seem to be an admission by the FCC that there will be interference.
I am sure others have spoken about the impracticalities of the mitigation measures for government devices. But
99% of America’s GPS receivers are not
government. The only thing in the order for them is scheme that has disruptions reported to the folks who might have caused the disruptions in the first
place.
Putting the fox in charge of guarding the hen house is very effective… but only for the fox.
Don’t get me wrong, the folks at Ligado are not bad people, I am sure. They are just trying to run a business. But it is very difficult to tell where any particular
problem with GPS reception is coming from. And none of us wants to be put in a position where we constantly have to resolve our own conflicts of interest.
So this is unfair to both Ligado and to America.
Monitoring and mitigating the projected interference is going to be a very difficult task if it is possible at all. Despite the
FCC’s dramatically reducing
its enforcement personnel and other resources in the last few decades, the commission is still legally responsible for spectrum enforcement and would be
most effective at this.
Your last item of tasking is to report on “other issues the study committee finds relevant.”
This reminds me of the “other duties as assigned” statement that used to come in every military officer’s job description.
It is a great opportunity for you, though, if you find things you think might improve the way the
FCC and others do things. It would be wonderful if you
can help prevent these kinds of problems from coming up in the future.
One thing, we need to do in the future, is to avoid Strother Martin’s “failure to communicate.”
The FCC as an organization had real communications problems in this case, some of which went beyond unconscious assumptions about technology and policy.
In 2003 the commission committed to not allowing stand-alone terrestrial service in the bands reserved for satellites.
Seven years and three FCC chairs later, the commission reversed itself by REQUIRING Ligado’s predecessor organization to establish a stand-alone terrestrial
service in the MSS L-band. This was part of its Harbinger-Skyterra Acquisition Order.
This requirement was a drastic change to the previous policy and to the entire satellite spectrum environment. It was such a change that before it was even
considered, it should have been the subject of a Notice of Proposed
Rulemaking. This would have included lots of engagement and formal dialog with
stakeholders.
None of this happened, of course, and that was a huge communications failure. By the way, we at the
RNT Foundation think that not doing a Notice of Proposed
Rulemaking was probably a violation of the Administrative Procedures Act and have said so in filings with the commission.
As you know there was all kinds of uproar as a result of the 2010 Harbinger Acquisition
Order. And you know that, as a result, the FCC put the whole issue
on hold in early 2012. Then, after another 7 years and another three FCC
chairs, and very little communications on the topic, the commission prepared to act again.
This time the administration’s communications on the issue were contradictory and confusing. On the one hand there was
NTIA, strongly supported by the
Secretaries of Defense and Transportation, and by senior staff at all relevant federal
departments. They formally established the executive branch’s
position as opposing the Ligado Networks
application.
On the other hand, very senior administration officials, including Larry Kudlow, director of the President’s National Economic Council, Mike Pompeo, the
Secretary of State, and William Barr, the Attorney General, all made high profile public statements in favor of approval.
One wonders what authority or expertise caused these government officials to believe it was appropriate for them to comment on a technical issue pending
before an independent regulator. I hate to think of the trouble I would have gotten into as a government official if I had done something like that.
This huge failure to communicate was a poster child for mixed messaging that harms citizens’ faith in government.
The FCC might have helped overcome this by including its Office of Economics and Analysis in the process.
The office was established in 2018 by Chairman
Pai as a direct result of the commission being criticized for a lack of transparency in its decision making, and for failing to assess and consider total
benefits and total costs to the nation of proposed actions.
Had the Office of Economics and Analysis reviewed the application, it would have compared the benefits to America of Ligado Networks using the spectrum as
proposed, and contrast that with the costs resulting from interference with existing
receivers. Given the tens of millions of GPS receivers likely impacted,
one would imagine than even marginal performance reductions, just by the sheer force of large numbers, would have made it very difficult to find a net
benefit to the nation.
But we don’t know for sure, because, even though this was a very complex, high profile case, the
FCC Chairman doesn’t seem to have ever asked that question.
Perhaps it was because he didn’t want to know the answer.
The Chairman and other Commissioners also never asked for classified briefings from the Department of Defense, despite having received two letters from the
Secretary of Defense. And, apparently, they gave no credence to a December 2019 letter from NTIA. Nor can I find any evidence they consulted with any
independent radionavigation experts to try to improve their understanding of what was clearly a tidal wave of concern across a huge number of technologies
and applications.
I am sure some folks at the FCC will tell you they had an official docket for comments and that they had appropriate communications before they made their
decision. But communication is more than just transmitting and receiving. It is having your messages understood and understanding what others are saying in
return.
Given where we are today, I have to conclude that, ironically, the Federal Communications Commission in this case had a significant failure to communicate.
So, we are in a very uncomfortable situation with two irreconcilable perspectives on an incredibly important issue. What do we do now?
I believe the FCC has an opportunity to do right by the nation by protecting space-based uses of spectrum while also recognizing Ligado Networks’ legitimate
interests. It can do this by restoring the space spectrum environment by swapping out Ligado’s current allocation for another set of frequencies that will
clearly not interfere.
I am reliably informed that this would not be unprecedented as similar exchanges have been done before. Also, that other suitable spectrum is available for
the exchange.
Not only will this eliminate the threat to space-based services, but it will also preserve the L band for future positioning, navigation, and timing use.
The U.S. is well behind China and others in PNT. I am told that L band is a sweet spot, and particularly useful for such applications.
I expect that Ligado might be happier with a different spectrum allocation as it wouldn’t be forever clouded by the threat of claims and lawsuits from GPS
users of all persuasions. I am not an attorney, but I would imagine that their current potential legal exposure is huge,
even if only a fraction of the
projected interference is realized. And that is without the RETAIN Act becoming law.
We all agree that it would be great if GPS signals weren’t so weak and
vulnerable. If there was something we could quickly do about the tens of millions of
vulnerable GPS receivers already in use for a wide variety of critical functions, many of them safety of life.
But that is not where we are. As much as we might like to, we can’t go back in time. We have to deal with the world as it is and improve things as much as
we can. Best of luck and Godspeed in your efforts, I am happy to answer questions if I have any time
remaining.
(January 2022) In-Car Jammers are Killing GNSS Integrity - GPS Patron:
https://gpspatron.com/in-car-jammers-are-killing-gnss-integrity/
(January 2022) ION congratulates Dana A. Goward, recipient of the Norman P. Hays Award given in recognition of outstanding encouragement, inspiration,
and support contributing to the advancement of navigation. (Please see his
recent January 2022 presentation above.)
(January 2022) Space Systems Command launches USSF-8 mission for US Space Force - GPS World:
https://www.gpsworld.com/space-systems-command-launches-ussf-8-mission-for-us-space-force/
(January 2022) Echoing the stated goals conveyed in this LinkedIn post: A Howard University Center, using a $5M grant from Mastercard, will train data
scientists who will work to eliminate biases in the financial sector and more. For an early precedent, where I pointed out a particular problem in planned
use of Neural Networks in evaluating real-estate mortgage applications, please see the following that alerts readers about the "likelihood of carrying over
human red-lining biases in NN implementations" in: Kerr, T. H., “A Critique of Neural Networks as Currently Exist for Control and Estimation,” Proceedings
of the International Conference on Signal Processing Applications & Technology (ICSPAT), Boston, MA, pp. 1434-1443, 24-26 Oct.
1995.
Also see:
Kerr, T. H., “Critique of Some Neural Network Architectures and Claims for Control and Estimation,” IEEE Transactions on Aerospace and Electronic Systems,
Vol. 34, No. 2, pp. 406-419, Apr. 1998. (an expose)
http://www.tekassociates.biz/CritiqueOfSomeNeuralNetworkClaims.pdf
(January 2022) A Chinese Satellite Just Grappled Another And Pulled It Out Of Orbit - The Drive:
Blog Editor's Note: This is a much smoother, even more menacing, demonstration of power in space and the ability to disrupt GPS/GNSS and other systems than
Russia's blasting a satellite to bits last year.
It shows much more capability and flexibility. And why would a country that expects to soon be the world's leading power both on the ground and in space
want to limit its options by creating more space debris?
A Chinese Satellite Just Grappled Another And Pulled It Out Of Orbit
The maneuver raises concerns about the potential militarization of satellites designed to inspect, manipulate, or relocate other satellites.
BY BRETT TINGLEY JANUARY 27, 2022
A Chinese satellite was observed grabbing another satellite and pulling it out of its normal geosynchronous orbit and into a “super-graveyard drift orbit.”
The maneuver raises questions about the potential applications of these types of satellites designed to maneuver close to other satellites for inspection or
manipulation and adds to growing concerns about China's space program overall.
On January 22, China’s Shijian-21 satellite, or SJ-21, disappeared from its regular position in orbit during daylight hours when observations were difficult
to make with optical telescopes. SJ-21 was then observed executing a “large maneuver” to bring it closely alongside another satellite, a dead BeiDou
Navigation System satellite. SJ-21 then pulled the dead satellite out of its normal geosynchronous orbit and placed it a few hundred miles away in what
is known as a graveyard orbit. These distant orbits are designated for defunct satellites at the end of their lives and are intended to reduce the risk
of collision with operational assets.
READ MORE: https://www.thedrive.com/the-war-zone/44054/a-chinese-satellite-just-grappled-another-and-pulled-it-out-of-orbit
(February 2022) Obituary for:
Langhorne McCook Bond, who led the Federal Aviation Administration during the Carter administration and prepared the agency with a detailed plan to manage
the air traffic controllers’ strike shortly after Ronald Reagan took office, died Jan. 29, 2022, in Marshall, after a long illness.
Mr. Bond was 84 years old and came from an aviation family. His father William Langhorne Bond – the subject of a book, China’s Wings, by Gregory Crouch – was
an aviation pioneer who led the China National Aviation Corp. and opened aviation in China before the Second World War.
One of the deadliest aviation accidents in U.S. history took place on Langhorne Bond’s watch at the FAA when an American Airlines McDonnell Douglas DC 10
crashed moments after takeoff from Chicago on May 25, 1979, killing all 258 passengers and 13 crew on board and two people on the ground. Maintenance issues
were ultimately found responsible for the crash, and inspired a passion for safety that led Mr. Bond to work on everything from safer helmets and protective
gear for horsemen to championing Loran and e-Loran as a backup system for the widely adopted Global Positioning System (GPS), which had been found to be
vulnerable to jamming. Both were pro bono activities for Mr. Bond.
While in college and law school, Mr. Bond and his friends Templeton Briggs and Alan “Pete” Day Jr. raced MGs on sport car circuits. Mr. Bond became aware of
equipment developed to make car racing safer, including important work by the Snell Memorial Foundation. Established in 1957 in memory of William “Pete”
Snell, a popular sport car racer who died in 1956 of head injuries during a race, the foundation created a new standard of safety for racing helmets.
Mr. Bond’s daughter Prescott was an avid equestrian, but after a fall that left her unconscious, he realized that riding helmets in the 1980s were only
shells and not protective. He joined forces with Drusilla E. Malvese, head of the safety committee of the Pony Clubs of America, to establish an ASTM 1163
certification for riding helmets. Ms. Malvese was able to get the helmet mandated for all children in pony club activities, but other horsemen were slow to
adopt the standard, particularly show circuit riders who did not like the “fatter” look of the helmets.
Over the years Mr. Bond, who chaired the Virginia Gold Cup International Steeplechase races in for 12 years, gave away dozens of helmets to steeplechase
riders, who eventually adopted the helmets for their own safety. Mr. Bond also worked to get safer breakaway rails for fences and to champion protective
vests for riders.
At an Air Traffic Control Association meeting in 1996, Mr. Bond raised the alarm that GPS needed a backup system because it was designed as a military
technology and could be turned off or jammed, leaving civil aviation at the mercy of military conflicts. This led to a personal partnership with Robert
Lilley and his wife Ellen, who were deeply involved with the International Loran Association (ILA). In the maritime industry, Loran, short for LOng RAnge
Navigation, can be used as potential backup technology for GPS, since it enables ships and aircraft to determine their speed and location using low frequency
signals broadcast from ground stations.
The original Loran-C system was decommissioned in 2010 despite the best efforts of Mr. Bond and the Loran association. At one time, an enhanced system –
eLoran – was expected to replace it with signals that, unlike GPS, could reach underground, underwater and into buildings. Mr. Bond spent countless hours
writing, testifying and advocating for Loran and eLoran as a backup system. Government agencies now appear to be supporting eLoran, and Mr. Bond’s hope was
that this system, used in Europe, will be adopted by the United States.
“Langhorne stood squarely for the principles of resilient critical infrastructure, in the face of the metaphorical oncoming trains when agencies teamed up
to delay the process,” said Mr. Lilley of the ILA. “It’s said frequently that ‘success has many fathers.’ When eLoran finally takes its place in the system
of systems, Langhorne can certainly claim a fair share of that parenthood. And he can know that his contributions are well remembered by our entire
community.” For his work on behalf of Loran, Mr. Bond was elected honorary fellow of the Royal Institute of Navigation in 2005 and made a life member of the
Resilient Navigation Timing Foundation in 2014.
Mr. Bond was born on March 11, 1937, in Shanghai, China, the elder of two sons of William Langhorne Bond of Petersburg, Va., and Katherine Dunlop of Chevy
Chase, Md. He graduated from Episcopal High School in Alexandria and attended the University of Virginia, receiving a BA in philosophy in 1959 and an LLB in
1963. Between college and law school, Mr. Bond carried out his military service and served as a member of the Virginia National Guard from 1959 to 1965.
After law school he did graduate work at the Institute of Air and Space Law, attended the Royal Aeronautical Society air transport course at Queens College,
Oxford, and studied the law of the sea (the basis for air and space law) at the London School of Economics.
Langhorne Bond began his career in 1965 as the special assistant to Alan S. Boyd, who was undersecretary of commerce for transportation, becoming his chief
assistant when Mr. Boyd became the first secretary of transportation in 1967. Mr. Bond became assistant administrator of the urban Mass Transportation
Administration before becoming the executive director of the National Transportation Center in 1969 in Pennsylvania.
Mr. Bond was recruited by Gov. Dan Walker to be secretary of transportation for the state of Illinois from 1973-77 and moved to Washington, D.C., when
President Jimmy Carter appointed him administrator of the Federal Aviation Administration, where he served from 1977-81. After leaving the administration,
Mr. Bond worked first as senior partner and then of counsel for the firm of Santarelli, Smith and Carroccio in Washington until his retirement in 1994. He
served as the president and chief executive officer of Shorts Aircraft USA from 1984-85.
Blog Editor's Note: The Hon. Langhorne Bond was a supporter of resilient navigation and timing long before establishment of the RNT Foundation.
In addition to the mentions in this obituary, he was one of our founding members. And, as part of his generous support, he co-hosted fabulous dinners for
our first three annual meetings.
He will be greatly missed.
A small correction to the comments in his obituary above about eLoran being used in Europe. The technology is currently being used by the UK (no longer
Europe?) for timing, and by China and South Korea for positioning, navigation, and timing (PNT). Older versions of Loran are in use by Russia, Saudi Arabia,
and Iran.
(February 2022) National Security Demands Better Govt PNT Leadership – UK expert’s paper at
RIN:
Blog Editor's Note: We have not see a lot of papers about PNT governance (other than our own), so it was great to receive this one from our colleague Andy
Proctor. He presented it at the Royal Institute of Navigation's (RIN) International Navigation Conference in November. It will be published in the conference
Proceedings.
We are glad to be able to share it here and also add a few additional words.
We particularly liked his mention of the Seven Pain Points of Systems of Systems, which we have reproduced below. This isn't a spoiler as he discusses how
to avoid or cope with them further in the paper. And there is a lot of other good stuff in there also.
SEVEN PAIN POINTS OF A SYSTEM-OF-SYSTEMS:
-INCOSE in its System Engineering handbook (INCOSE, 2015) set out the typical challenges and conflict area between the
SoS activities and the constituents.
These are summarised and recounted below as “seven pain points” and must be addressed in any SoS development, especially in an Enterprise or Governmental
setting. SoS Authority and Governance. In a SoS each constituent system has its own ‘owner’, stakeholders, users, processes, and business model. There is a
heavy reliance on an agreed common purpose and motivation for constituents to work together towards collective objectives which may or may not coincide with
those of the constituent systems.
-Leadership. The lack of common authorities and funding pose challenges for SoS especially for leadership, coherence, and direction in a
multi-organizational
environment.
-Constituent systems’ perspectives. SoS are typically comprised, at least in part, of in-service systems, which were often developed for other purposes and
are now being leveraged to meet a new or different application with new objectives. This is the basis for a major issue facing
SoS's; that is, how to
technically address issues which arise from the fact that the systems identified for the
SoS may be limited in the degree to which they can support the SoS.
-Capabilities and Requirements. Ideally engineering processes begins with a clear, complete set of user requirements and provides a disciplined approach to
develop a system to meet these requirements. Typically, SoS are comprised of multiple systems with their own requirements, working towards broader capability
objectives. Ideally the SoS capability needs are met by the constituent systems as they meet their own requirements, but in many cases the
SoS needs may not
be consistent with the requirements for the constituent systems. In these cases, the
SoS needs to identify alternative approaches through changes to the
constituent systems or additions of other systems to the SoS. This is a significant challenge for
PNT systems due to the diverse nature of the use cases
where PNT is essential.
-Autonomy, Interdependencies and Emergence. An independent constituent system may change independently of the
SoS, along with interdependencies between that
constituent system and other constituent systems which adds to the, and introduces complexity or unknown elements in, the
SoS. Specifically, this can lead
to unanticipated effects at the SoS level leading to unexpected or unpredictable
SoS behaviour.
-Testing, Validation, and Learning. The fact that SoS are typically composed of constituent systems which are independent of the
SoS poses challenges in
conducting end-to-end SoS testing as is typically done with systems.
-SoS Principles. SoS is a relatively new area, with the result that there has been limited attention given to ways to extend systems thinking to the issues
particular to SoS. Work is needed to identify and articulate the cross-cutting principles that apply to
SoS in general, and to developing working examples
of the application of these principles. There is a major learning curve moving to a SoS environment, and a problem with
SoS knowledge transfer within or
across organizations.
Link to paper: DEVELOPING A PNT ARCHITECTURE FRAMEWORK: https://rntfnd.org/wp-content/uploads/Developing-a-PNT-Architecture-Framework-Proctor.pdf
(February 2022) U.S. Navy-Chartered Ordnance Barge Runs Aground on Florida Beach:
https://lnkd.in/g7SzsSsR
https://www.maritime-executive.com/article/u-s-navy-chartered-barge-carrying-ordnance-runs-aground-off-florida
(February 2022) Asteroid sharing Earth’s orbit discovered – could it help future space missions?:
Research has shown that the Earth trails an asteroid barely a kilometre across in its orbit about the Sun – only the second such body to have ever been
spotted. It goes round the Sun on average two months ahead of the Earth, dancing around in front like an excited herald of our coming.
https://theconversation.com/asteroid-sharing-earths-orbit-discovered-could-it-help-future-space-missions-176272
(February 2022) Space Force extends L3Harris’ contract to upgrade space tracking system:
https://spacenews.com/space-force-extends-l3harris-contract-to-upgrade-space-tracking-system/
(February 2022) Comment by James Kiessling, Systems architect and analyst:
I suggest that the USAF allowed ego's and 'command' attitudes get in the way of a proper make or buy decision regarding
JMS. They also kept revising the
delivery requirements downward when their team failed to make schedule or technical product standards. On the other hand, cloning the commercial product
bought by the Brits would have done 90% of the job before any customization work. It makes me believe that the decision making process and selected decision
makers are the problem - not the solution.
(February 2022) Comment by David Finkleman, Chief Engineer at SkySentry,
LLC:
For Marco, there are (or were) comprehensive publications that reveal the content of a TLE. I think my paper, “TLE or not TLE. That is the question!”
Includes such. That was more than 15 years ago. Tom is on point. He lived with some of that, too. There is much more detritus, such as the “obs” used to
derive TLE’s not being the actual observations. They are also correlated, extracted from the filtered sensor track. Returning to Marco, there are several
archaic (even useless) TLE fields. For example the checksum, long since overshadowed by comm protocols and error correction. Each system iteration
essentially reestablished the old processing scheme in “modern” hardware and system software. Why? Two reasons. First, almost no one involved knows how
TLE’s are developed from obs, the basic theory, and limitations. Decision makers are afraid to change anything because they fear the consequences. Second,
the major changes required would cause contract mods and greater overruns. The unknowing decision makers know well that changes cost money, not realizing
the cost of not changing. A sad state of affairs caused by ignorance, fear, and BTW secrecy.
(February 2022) Comment by Dennis Bangham, Senior Systems Engineer at Northrop Grumman Strategic Space Systems Division:
It is normal operating procedure to relax or waive the requirements in order to meet schedule. That is how the PM are judged and promoted.
(February 2022) Comment by Tom Johnson, CEO and Founder at Exa Research:
There was zero chance that a "buy" decision would occur in JMS. The few commercial companies that managed to crowbar their way into the program consistently
had their solutions deferred to later service packs, and lo and behold - the money ran out because of the legacy contractors failure to deliver on the
fundamentals of the earlier service packs.
Commercial solutions were (and still are) available and running operationally.
(February 2022) Comment by Dennis Bangham Yes - and that sad state of affairs is why uniforms have a poor track record in acquisition.
Need actual professionals who will stay with the program from inception through delivery - rotating PMs is the worst imaginable system.
(February 2022) GPS-Independent Navigation at the Core of Space Development Agency’s New LEO Constellation - Navigation Outlook:
Blog Editor's Notes: First and foremost, congrats to our friend, colleague, and award winning journalist Dee Ann Divis for standing up her new site and
newsletter "Navigation Outlook." She always has great insights and often exclusive stories you will find there first. We highly recommend signing up.
We were intrigued by the article below, some of which was reprinted in the Winter 2022 ION Quarterly Newsletter. Particularly that
Space Development Agency
(SDA) is looking for partners in its endeavor. At least two companies, Trustpoint and Xona Space Systems (an
RNTF supporter), are already a ways down the
road toward their own LEO PNT systems. We wonder if companies like these are what
SDA is thinking about for partnering...
Also of note is that the constellation will initially rely on GPS for its operation, as is the case for most all
comms/LEO constellations. PNT is slated for
later in the program. We are thinking that schedule will allow SDA to keep its options open longer.
Shawn Brennan, Air Force Veteran / Outdoor Enthusiast:
Intriguing. I’m just having trouble separating truth from marketing.
If the system has laser comm cross links as planned, then implementing system-determined
PNT is somewhat straightforward. Not simple, but the math and
physics are known. (Plenty of others have worked on this, including concepts that leveraged the existing
GPS-NDS cross links and others that presumed the
original GPS III concept’s crosslinks.) I am interested to hear how many satellites they would need in
LEO in order to become self-determining. (I’m also
interested in whether they plan to use m-code receivers, or if they are using their prototype designation to skip that part, or if they are planning on
software defined receivers.)
Elsewhere in the article where they imply they are looking at becoming an Alternate PNT source for other users I get a little more skeptical. We’ve seen
pieces of this in other space tech news, but either they have a workable concept they are shooting for, or they don’t. Which is it?
(February 2022) Russian Anti-Satellite Threats Against GPS - ION Newsletter:
Blog Editor's Note: A very good column by Doug Taggart who writes "Defense Matters" for the quarterly ION Newsletter. And we love the sub-head "Just Saber
Rattling - It is... until it isn't."
Most of this thoughtful piece is about space debris,. It should be required reading for everyone concerned about space operations and assets.
His saber rattling comment, though, caused us to think about Russia's calculus and whether or not they might actually move against
GPS.
Some questions to consider listed in no particular order:
-In a conflict, or leading up to one, could Russian leaders convince themselves that an attack on
GPS is a justified tactical maneuver rather than a
strategic, near existential stroke?
-How would the US respond to a kinetic attack on GPS satellites?
Russia reportedly has nuclear powered EW satellites in place that can disable
GPS and other satellites either temporarily or permanently. How might the U.S.
response to a serious EW attack differ from its response to a kinetic attack?
-Russia is far less dependent on GNSS than the U.S. - Would the U.S. response to a Russian attack on
GPS have to be be more than an just attacking GLONASS?
-Could Russia launch a kinetic attack against GPS sats that would create minimal space debris?
Russia wants to be at least a peer of China and the U.S., but has clearly fallen into third place in the world. If they felt they were falling further
behind, or were in extremis during a conflict, would they sacrifice safe operations in
MEO, or maybe even write off MEO altogether, in order to regain
status in the world?
-Could Russia mount kinetic or EW attacks on GPS satellites that would be difficult or impossible to trace back to them?
We are sure (or at least we hope) the National Security Council is asking itself these kinds of questions.
Perhaps they should also ask themselves "How can we get the bullseye off (of) GPS?"
Russian Anti-Satellite Threats Against GPS -
Just Saber Rattling? – It is…until it isn’t.
Doug Taggart, President, Overlook Systems Technologies, Inc.
On November 15th, Russia tested a direct-ascent, anti-satellite
(DAASAT) missile that struck one of its own satellites in Low Earth
Orbit (LEO) and created
a large debris field. The U.S. Space Command’s Public Affairs Office reported that the test had “…generated more than 1,500 pieces of trackable orbital
debris and will likely generate hundreds of thousands of pieces of smaller debris.”
“Russia has demonstrated a deliberate disregard for the security, safety, stability, and long-term sustainability of the space domain for all nations,” said
U.S. Army Gen. James Dickinson, U.S. Space Command commander in the statement. “The debris created by Russia's
DA-ASAT
will continue to pose a threat to activities in outer space for years to come, putting satellites and space missions at risk, as well as forcing more
collision avoidance maneuvers. Space activities underpin our way of life and this kind of behavior is simply irresponsible.”
READ MORE (starting on page 14): https://www.ion.org/newsletter/upload/ION-Winter22.pdf
(February 2022) Pentagon Launching New Hypersonic Ballistic Tracking Space Sensor (HBTSS) Technology:
https://warriormaven.com/global-security/hypersonic-ballistic-tracking-space-sensor-hbtss
https://navoutlook.com/gps-independent-navigation-at-the-core-of-space-development-agencys-new-leo-constellation/
(February 2022) Lawsuit - 'Ligado's predecessor withheld interference info' - Navigation Outlook:
Blog Editor's Note: For those who haven't closely followed the twists and turns of the
LightSquared/Ligado/Federal Communications Commission
(FCC) soap
opera over the decades, this chapter might be quite the surprise.
It seems that in one of Ligado's predecessor companies, an outfit called Mobile
Satellite Ventures (MSV), discovered in 2001 that planned transmissions would
interfere with some GPS receivers. Yet this information was withheld from both the FCC and companies that subsequently acquired MSV's assets.
One of those companies was Harbinger Capital Partners which formed and owned LightSquared.
In 2017 Harbinger filed a lawsuit against Apollo Global Management, the company from which they purchased the former
MSV 's assets. The suit alleged that not
disclosing the 2001 interference study constituted fraud. LightSquared eventually went bankrupt and was reformed into Ligado.
Harbinger's lawsuit was dismissed without prejudice in 2019, meaning they could refile at any time. The news item below posted by our alert colleague and
friend, Dee Ann Divis, is that the lawsuit is back on.
Another important aspect to all of this is that MSV violated FCC rules when they failed to disclose the interference study in a 2003 application.
RNT
Foundation has raised this issue to the Commission twice. In 2020 we requested the Commission reconsider its
Ligado Networks decision for several reasons,
including this one. We said:
3. Ligado’s Predecessor-in-Interest Apparently Withheld Material Information Crucial to the Commission’s Proceeding
The applicant appears to have been derelict, at best, in following Commission rules. In December 2017, in a lawsuit filed against former directors of
SkyTerra (Apollo Global Management, et. al.) by Harbinger Capital Partners, it was alleged that
Ligado’s predecessor-in-interest, Mobile Satellite Ventures
(“MSV”), had performed testing in 2001 that showed potential receiver overload interference to
GPS receivers.[1] This appears to have been the case as
evidenced by an October 10, 2001 briefing titled “Desensitization Performance of
GPS Receiver and MSV System Implications” that was contained in a U.S.
Patent and Trademark Office filing referenced in the Harbinger lawsuit. This information, and a request that the Commission consider this issue, was
entered in the Ligado docket by the Resilient Navigation and Timing
Foundation in March of 2018.[2]
Failing to disclose material information appears to be a violation of the Commission’s rules.[3] Commission officials, in Congressional testimony in
September 2012[4], indicated the Commission had no knowledge of the GPS
receiver overload issue until it was raised by GPS interests in
2010. It appears
that information material to the Commission’s decision in March 2010 in the Harbinger Acquisition Order may have been withheld by
Ligado’s
predecessors-in-interest in violation of Commission rules that are fundamental to its regulatory decision-making process. The aforementioned testing in
2001 preceded adoption of initial MSS ATC rules by the Commission in 2003 and the initial license grant to
MSV (now Ligado) in 2004 to provide MSS ATC
service. Despite this being entered into the docket by the Resilient Navigation and
Timing Foundation, the Commission’s final Order failed to address
this important issue.
We request the Commission stay its Order and direct an independent investigation into this issue. If the investigation shows that information the applicant
or a predecessor-in-interest knew or had reason to know was withheld, we request the Order be reversed with prejudice.
[1] https://ecfsapi.the Commission.gov/file/103201383000922/RNT%20Foundation%20ex%20parte%20THE COMMISSION%20-%20Ligado%20MSV%20failure%20to%20disclose.pdf
[2] https://ecfsapi.the Commission.gov/file/103201383000922/RNT%20Foundation%20ex%20parte%20THE COMMISSION%20-%20Ligado%20MSV%20failure%20to%20disclose.pdf
[3] (Truthful and Accurate Statements to the Commission, THE COMMISSION rule Part 1.17)
[4] See Joint Written Statement of Julius P. Knapp Chief, Office of Engineering and Technology, Mindel De La Torre, Chief, International Bureau, Federal Communications Commission,
Before the House Oversight and Investigations Subcommittee, Energy and Commerce Committee, U.S. House of Representatives “The LightSquared Network: An Investigation of the THE
COMMISSION’s Role” (Sept. 21, 2012).
RNTF's 2020 Petition for Reconsideration, along with petitions from six other groups, is still pending before the
FCC.
The below article discusses the new lawsuit's possible impacts on future actions by Congress and the
FCC.
READ MORE: https://navoutlook.com/judge-to-hear-new-arguments-as-6b-lawsuit-continues-over-alleged-concealment-of-gps-interference-issues/
(February 2022) Russian Anti-Satellite Threats Against GPS - ION Newsletter:
Blog Editor's Note: A very good column by Doug Taggart who writes "Defense Matters" for the quarterly ION Newsletter. And we love the sub-head "Just Saber
Rattling - It is... until it isn't."
Most of this thoughtful piece is about space debris,. It should be required reading for everyone concerned about space operations and assets.
His saber rattling comment, though, caused us to think about Russia's calculus and whether or not they might actually move against GPS.
Some questions to consider listed in no particular order:
-In a conflict, or leading up to one, could Russian leaders convince themselves that an attack on GPS is a justified tactical maneuver rather than a
strategic, near existential stroke?
-How would the US respond to a kinetic attack on GPS satellites?
Russia reportedly has nuclear powered EW satellites in place that can disable GPS and other satellites either temporarily or permanently. How might the U.S.
response to a serious EW attack differ from its response to a kinetic attack?
-Russia is far less dependent on GNSS than the U.S. - Would the U.S. response to a Russian attack on GPS have to be be more than an just attacking GLONASS?
-Could Russia launch a kinetic attack against GPS sats that would create minimal space debris?
Russia wants to be at least a peer of China and the U.S., but has clearly fallen into third place in the world. If they felt they were falling further
behind, or were in extremis during a conflict, would they sacrifice safe operations in
MEO, or maybe even write off MEO altogether, in order to regain
status in the world?
-Could Russia mount kinetic or EW attacks on GPS satellites that would be difficult or impossible to trace back to them?
We are sure (or at least we hope) the National Security Council is asking itself these kinds of questions.
Perhaps they should also ask themselves "How can we get the bullseye off (of) GPS?"
Russian Anti-Satellite Threats Against GPS -
Just Saber Rattling? – It is…until it isn’t.
Doug Taggart, President, Overlook Systems Technologies, Inc.
On November 15th, Russia tested a direct-ascent, anti-satellite (DAASAT) missile that struck one of its own satellites in
Low Earth Orbit (LEO) and created
a large debris field. The U.S. Space Command’s Public Affairs Office reported that the test had “…generated more than 1,500 pieces of trackable orbital
debris and will likely generate hundreds of thousands of pieces of smaller debris.”
“Russia has demonstrated a deliberate disregard for the security, safety, stability, and long-term sustainability of the space domain for all nations,” said
U.S. Army Gen. James Dickinson, U.S. Space Command commander in the statement. “The debris created by Russia's
DA-ASAT
will continue to pose a threat to activities in outer space for years to come, putting satellites and space missions at risk, as well as forcing more
collision avoidance maneuvers. Space activities underpin our way of life and this kind of behavior is simply irresponsible.”
READ MORE (starting on page 14): https://www.ion.org/newsletter/upload/ION-Winter22.pdf
(February 2022) Russia expected to ditch GLONASS for Loran in Ukraine invasion - GPS World:
Blog Editor's Note: This makes all kinds of sense.
Another thought - Russia has a huge military presence in Syria. If they were to establish a
Chayka/Loran station there, it could extend coverage to the
whole Eastern Mediterranean. An area for which the U.S. Maritime Administration is always issuing advisories for
GPS jamming and spoofing.
Russia expected to ditch GLONASS for Loran in Ukraine invasion
February 17, 2022 - By Tracy Cozzens
Russian military doctrine assumes GLONASS and other GNSS will not be available once a battle begins, so will instead turn to
Loran-C for navigation
Russian forces are expert at jamming and spoofing GNSS. As a result, military analysts say, Russian military doctrine assumes that signals from space,
including it’s own GLONASS and other GNSS, will not be available once a battle begins.
According to the Russia and CIS Radionavigation Plan, the terrestrial Chayka
system, a version of Loran-C, is maintained to protect their homeland with
navigation and timing services when signals from space are not available. The portable
Skorpion system is designed for military use during expeditions to
areas where Chayka or Loran is not available, according to western military analysts.
“Fixed Chayka transmission sites operate between 90 Khz and 110
Khz. Power output is typically between 200 and 800 kW with effective ranges over land of,
respectively, about 800 miles and over water of 1,000 miles,” explained Dana Goward, president of the Resilient Navigation and Timing Foundation. He noted that little
information is publicly available about the military Skorpion system.
“Three of Russia’s Chayka/Loran stations have Ukraine surrounded,” explained UrsaNav CEO Charles Schue, referring to a graphic he provided
GPS World. “They
provide ideal coverage and will allow navigation accuracy of between 20 and 50 meters over most of the
Ukraine. Upgrading to an eLoran equivalent could
give them 5-to-10-meter accuracy, but I am sure the current setup is more than adequate for their purposes at the moment.”
READ MORE: https://www.gpsworld.com/russia-expected-to-ditch-glonass-for-loran-in-ukraine-invasion/
(February 2022) The True Value of Inertial Navigation - An Interview with Brad Parkinson - GPS World:
The True Value of Inertial Navigation
An Interview with Brad Parkinson
By Dana Goward, President, Resilient Navigation and Timing Foundation
A U.S. Secretary of Defense once predicted that navigation would eventually be based on inertial devices that were set at the factory and then always knew
where they were forever after. Recently published research has reported on steps in that direction.
But according to navigation expert Brad Parkinson, the outlook is not as bright as some might think.
RNT Foundation President Dana A. Goward recently discussed the issue with him.
Goward – Dr. Parkinson, you are well known for your contributions as the chief architect of the
Global Positioning System. But you have more than a passing
familiarity with inertial systems also, is that right?
Parkinson – I do. Long before I was involved in radio navigation, I was the Chief Analyst for all the USAF testing of inertial navigation systems. I did my
masters in Doc Draper's Inertial Lab at MIT in 1961.
I am a major advocate and defender of Inertial systems. I also have in-depth understanding of their limitations.
Goward – Have you been following the recent media coverage about advances with inertial systems?
Parkinson - I enjoy reading about these advances in physics devices. At the same time, I am a little impatient with media articles which do not appreciate
the differences between building a device that measures specific force (or senses rotation) and a working inertial navigation system.
Goward – What are some if the inherent limitations of these systems?
Parkinson – I find it interesting that some of the articles speculate they may be able to supplant GPS and other GNSS. There is no way an inertial navigation
system, even with perfect gyros and force sensors, can provide the accurate position (say better than 10 meters) after extended periods (hours to days). In
fact, attaining better than 200 meters accuracy after a few hours will be very difficult in a moving vehicle.
Today, farmers require even greater accuracy from GPS. They routinely use GPS for row operations, with accuracies of a few centimeters. The economic value
is indirectly measured by the farmer's purchase of such equipment – the agriculture market for GPS equipment is well over a billion dollars a year. Thus, a
general replacement for GPS has to provide centimeter accuracies.
Goward – So what is it about inertial systems that stand in the way of them becoming autonomous substitutes for GPS?
Parkinson - There are some very simple and fundamental reasons that inertial positioning systems cannot hope to deliver such capability:
First, force sensors are not accelerometers. To find acceleration, one needs to add vector gravity to their outputs. But gravity, or “g force” varies a lot
at the micro g levels and the inaccuracies are fed to the double integration that produces position. Errors grow as time or time squared and, without outside
reset, are essentially unbounded. The physics devices described in some of these articles are definitely instruments that Doc Draper described as "Specific
Force Sensors".
What we loosely call "g force” or just “g,” is actually the inverse of the reaction to maintain stationarity on the earth. "g" is defined to include the
centrifugal force due to earth's rotation which varies greatly as a function of Latitude - the radius of the merry-go-round called earth. Mountains and
chasms affect the local g. Further, it is a vector quantity: Its direction can change locally by many arc seconds. In a word, down does not generally point
to the center of the earth. Gravity gradiometers might be of limited help, but they are very large and not made for dynamic environments.
In a nutshell, these devices cannot sense gravity. It must be calculated and added to the three-dimensional specific force sensor to estimate acceleration.
Second, to use these devices for extended navigation, coordinate frames would have to be defined and stable to milli-arc seconds. All instruments would have
to have input axes and cross axis sensitivity calibrated to corresponding levels. Generally, this problem is ignored in many lab projects.
Third, for inertial navigation sensors to work, they need to accurately know their initial position. Any initial velocity or position errors will grow as a
function of time.
Fourth, the vertical position axis is inherently unstable and diverges exponentially.
Physicists have been enamored with instruments which can use atoms to sense specific force and rotation. While scientifically interesting, even if perfect
they cannot overcome these challenges.
Goward – But there is still a role for inertial systems in navigation, isn’t there? How good are they and what are some of the applications?
Parkinson - I suspect the best inertial systems of today (which are in nuclear submarines) can do about 0.1 nautical miles or about 200 meters for a few days.
I am sure the real number is classified. These systems are very large, expensive, and complicated. They rely on a very low acceleration environment and are
periodically reset with GPS. And they probably use gravity gradiometry to calculate the local variations in gravity to the first order. They do not calculate
the vertical position and use water density and knowledge of the local geoid to keep the vertical axis stable.
An aircraft with inertial can, to some extent, with knowledge from elsewhere of local sea level barometer settings, and by assuming adiabatic pressure
variations, keep the vertical dimension errors bounded.
I strongly support the Inertial/GPS/Directional Antenna marriage for users who want assured PNT. Aviation is a good use case for this. Inexpensive inertial
components (called MEMS) can improve the jamming resistance of the GPS receiver by 15 dB or more. This step alone can reduce the effective line of sight
jammer denial area by over 95%.
Goward – So inertials can be a good part of solutions, but aren’t necessarily the whole solution themselves.
Parkinson – Exactly. Despite what some media outlets might publish as a way to lure in readers.
(March 2022) GPS Jamming in Ukraine - Space News & Breaking Defense:
Blog Editor's Note: Two timely articles today.
Pretty easy guess that jamming GPS would be a part of the Russian invasion. The question really is about scope. It seems to be localized, so far.
And, as the second article points out, "Thank you for that, Mr. Putin. It allows
NATO to do things next door much more easily than otherwise." It also
points out that Russia may well jam more broadly later.
As far as we know, the Pentagon does not have a program of persistent monitoring for
GPS disruption around the globe. The USCG does receive reports and
posts them. DOD is looking into using commercially available information (we are guessing
AIS and ADS-B) to identify such disruptions. But those two efforts
seem to be the extent of it.
HawkEye 360 detects GPS interference in Ukraine
by Debra Werner — March 4, 2022
Updated March 4 at 10:40 am Eastern time with comments from HawkEye 360 CEO John Serafini.
GPS radiofrequency interference can signal impending military activity.
HawkEye 360 proved that point in a March 4 news release on GPS interference in and around Ukraine over the last four months. Prior to Russia’s Feb. 24
invasion of Ukraine, the Herndon, Virginia-based geospatial analytics company noted continual and increasing
GPS interference near Ukraine.
“This is a modern war, with the Russians leveraging the latest in electronic warfare technologies,”
HawkEye 360 CEO John Serafini told SpaceNews by email.
“This is representative of the tactics that Russian troops are deploying to degrade the effectiveness of space-based
assets, such as the United States Global
Positioning System. GPS jamming is one facet that we are seeing evidence through the use of our signal detection constellation and processing capabilities.”
READ MORE: https://spacenews.com/hawkeye-360-gps-ukr/
‘Local’ Russian GPS jamming in Ukraine hasn’t affected US support ops, so far
The Pentagon doesn't believe Russia has fully unleashed its significant electronic warfare capabilities, a senior defense official said.
By THERESA HITCHENSon March 01, 2022 at 2:43 PM
WASHINGTON: Localized Russian jamming of GPS signals in Ukraine has been detected by US forces in the region, but so far has not interfered with US support
operations, according to Pentagon officials.
One military source told Breaking Defense that jamming has been detected as far out as the Black Sea by US reconnaissance aircraft, but the source stressed
it hasn’t had any adverse impact on mission capability [yet].
Similarly, when asked about Russian jamming, a US Space Command spokesperson said, “There are no impacts to U.S. and Allied forces in Europe at this time.”
That said, a senior defense official told reporters today that the US suspects Russia has been holding back in utilizing its vast toolset for electronic
warfare so far.
READ MORE: https://breakingdefense.com/2022/03/local-russian-gps-jamming-in-ukraine-hasnt-affected-us-support-ops-so-far/
(March 2022) Strategic Russian GPS Jamming in Baltic - Info from "The Guardian":
Blog Editor's Note: We think The Guardian missed the point on the story below, so we created our own headline for this post.
Reading the article carefully reinforces the idea that the Russian government coordinates most of its interactions with the outside world very carefully.
Ostensibly the article is about aircraft flying over Kaliningrad and experiencing interference with
GPS reception. Stepping back one or two paces though,
one notices several other items in the report that fit into a recent overall pattern of Russia trying to regain regional and world dominance. Several
things to note:
The interference began right after the Finnish president met with President Biden. Recall that Putin recently threatened Finland and Sweden with invasion
if they sought to join NATO.
The jamming in Finland's east has caused flights to be cancelled. Certainly an expression of Russian power to, with the flip of a switch, cause Finnish
commercial flights to be cancelled. Another point for our readers to note is that, despite having terrestrial navigation aids, commercial flights are still
often cancelled when GPS is not available for whatever reason.
This is not just about Finland - it is Russia flexing its muscles for the whole region.
GPS interference from the Russian province of Kaliningrad.
Kaliningrad is bordered by NATO members Poland and Lithuania (see map courtesy Shutterstock). Between Kaliningrad and Finland lie the only former Soviet
states that are now NATO members - Lithuania, Latvia, and Estonia. So, "Nice aviation system ya got there, former states. Would be a shame if anything
happened to it."
It is also about Europe writ large. Note in the article that most European flights pass over or near Kaliningrad, so all have the opportunity to experience
disruption.
Finland reports GPS disturbances in aircraft flying over Russia’s Kaliningrad
The interference began soon after a meeting between presidents Sauli Niinistö and Joe Biden
Aircraft flying near the Russian enclave of Kaliningrad and near Finland’s eastern border with Russia have noticed interference with their
GPS signals,
according to Finnish authorities.
The interference began soon after Finland’s President Sauli Niinistö met Joe Biden in Washington on Saturday to discuss deepening defense ties between
Finland and NATO due to Russia’s attack on Ukraine.
Prime Minister Sanna Marin told Reuters she had no information about the source of the disturbances, nor about whether they originated in Russia, while the
foreign ministry said it was looking into the events.
https://www.theguardian.com/world/2022/mar/09/finland-gps-disturbances-aircrafts-russia?CMP=Share_iOSApp_Other
(April 2022) Earth is layered like an onion, with a thin outer crust, a thick viscous mantle, a fluid outer core and a solid inner core. Within the mantle,
there are two massive blob-like structures, roughly on opposite sides of the planet.
The blobs, more formally referred to as Large Low-Shear-Velocity
Provinces (LLSVPs), are each the size of a continent and 100 times taller than Mt. Everest. One is under the African continent, while the other is under
the Pacific Ocean.
Using instruments that measure seismic waves, scientists know that these two blobs have complicated shapes and structures, but despite their
prominent features, little is known about why the blobs exist or what led to their odd shapes.
(April 2022) Blog Editor's Note: Open source information about the ability to detect GPS/GNSS interference from space has been available for a
while:
It is good to see several DOD efforts to collect it.
All systems have their limitations, though. Collection from space has a hard time detecting lower power emitters (of course) and pinpointing sources. Using information
from systems like AIS and ADS-B can better locate sources, but are still far from sufficient to allow authorities to go to an address and confiscate equipment.
We are guessing it will be a while before space-based assets can provide sufficiently precise locations to help
DOD "...readily identify these sources of interference
and correct any potential problems before they become a threat." It seems to us that things like this are important in terms of
DOD developing and displaying a strategic
picture. We aren't sure, though, how they could support tactical military or law enforcement operations.
Spire Global Inc., a provider of space-based data, analytics and space services, is using its constellation of about 40 geolocation satellites to detect
GPS jamming.
Spire is collecting data for use by the U.S. Space Force, a particularly important task in light of Russia’s invasion of Ukraine.
“All of our fellow space companies… everyone is playing a vital role for humanity in this battle for freedom and democracy,”
Spire CEO Peter Platzer told analysts
March 9 in an earnings call, according to Space News.
https://spacenews.com/space-force-using-spire-data-to-detect-satellite-jamming/
(April 2022) Airlines Report Russian GPS Jamming In Four Regions:
Blog Editor's Note: There have been A LOT of articles about this recently, so we felt compelled to pass this one along.
We have to note, though, that EUROCONTROL and the US Maritime Administration have been complaining and warning about GPS disruption in the Eastern
Mediterranean for years. Also, the Black Sea has long been a hot spot for spoofing and other disruptions. We first reported on this in 2017 and
C4ADS did their
big report in 2019. And, this isn't the first time, or even the second, we have read about Russia interfering with
GPS signals in the Baltic and Scandinavia.
We are pretty sure that all the press is because (a) Russia has stepped up its jamming because of the war, and (b) the war has caused folks to be more concerned
about things that have been happening to some degree all along.
https://www.flyingmag.com/airlines-report-russian-gps-jamming-in-four-regions/
(April 2022) Re: The Armada Article addressing Russian Chayka use in Ukraine:
While Editor found the article interesting and am glad to see some recognition of the value of high power/low frequency
position, navigation, and timing (PNT) systems to ensure
resilient PNT services, I was struck by the coverage map that was provided in the article. Using my mapping program to duplicate the size of the coverage circles depicted in
the article, it would appear that the author estimated the coverage area of each Chyka station to be a circle with a radius of approximately 250 statute miles. In actuality,
the coverage of such a station should easily be twice that radius and, depending on other factors, perhaps quite a bit more depending on the required performance metrics of
the application.
One factor that can affect position performance is, of course, the geometry of the stations. In the case of Ukraine, it would appear that the three Chyka stations were placed
at uniquely ideal locations to take advantage of their PNT services — notably the one in Crimea that Russia regained control of when they annexed the peninsula.
It continues to interest and concern me that although both Russia and China see the need and importance to maintain their resilient high power/low frequency
PNT solutions,
despite both operating their own GNSS constellations, the Western nations (i.e., the U.S., Canada, Western Europe, and Japan) abandoned theirs
(Loran-C) a decade ago and, despite
the recommendations from many, many PNT Subject Matter Experts, never pursued
eLoran as the natural resilient PNT follow-on. Only Saudi Arabia and
South Korea have had the
good sense to both maintain and improve their Loran capabilities.
As someone who grew up in the 20th century, I continue to be quite amazed that the most critical decisions about how to protect and defend our critical infrastructure are
dictated by financial analysts, rather than those directly responsible for the safety, security, and economic benefits of the Nation. As a systems engineer, my perception
is that user needs drive requirements drive development of solutions and that the financial offices’ role is to provide the resources necessary to enact these strategic
decisions. Because these roles shifted so drastically over the past twenty years, we find ourselves in a much more perilous position and needing to “catch up” to others who
had the good sense to recognize the value of resilient and robust and complimentary
PNT solutions. As we continue to explore new means of hardening signals from space in all
orbital planes, I sincerely hope that the relatively small amount of resources needed to restore our ground-based
PNT infrastructure is made available and, by including
new innovations, we can restore a system that will more than prove its value to land, air, and sea users in the 21st century.
Best regards,
Mitch Narins, CISSP®/ FRIN
Principal Consultant / Owner
mitch@strategicsynergiesllc.com
(April 2022) Radar Technology Pioneer Merrill Skolnik Dies at 94:
-First recipient of the IEEE Dennis J. Picard Medal
-Life Fellow, 94; died 27 January
Skolnik served as superintendent of the radar division of the U.S. Naval Research Laboratory in Washington, D.C., for more than 30
years. While there, he made significant
contributions including helping to develop high-frequency, over-the-horizon radar; a system that can identify friend or foe during combat; and high-resolution radar
techniques.
For his work in the field, he was named the first recipient of the IEEE Dennis J. Picard Medal for Radar Technologies and Applications, in
2000. Picard was chief executive of
Raytheon and helped the company become a leader in tactical missile systems.
Skolnik began his career in 1955 at MIT’s Lincoln Laboratory. While there, he taught a course on radar at Northeastern University, in Boston. The course was the basis for his
1962 book Introduction to Radar Systems.
He left MIT in 1959 to join Electronic Communications, now part of Raytheon. There he gained experience working on antennas, electronic warfare, and phased arrays.
He then joined the Institute for Defense Analyses, in Alexandria, Va. It provides technical advice to the
U.S. Defense Department, the Defense Advanced Research Projects
Agency, and other government entities. While there, he did pioneering work on thinned arrays and
self-phasing array antennas. He also contributed to the fields of bistatic
radars and electronic countermeasures.
In 1965 he became superintendent of the radar division at the U.S. Naval Research
Laboratory. He and his staff developed concepts for wideband shipboard air-surveillance
radar with reduced susceptibility to electronic countermeasures; self-defense radar; and space-borne radar for detecting ships.
He continued to work as a consultant for the lab after he retired in 1996.
In 1944 Skolnik joined the American Institute of Electrical Engineers, one of IEEE’s predecessor societies. He served on the
Proceedings of the IEEE editorial board in
the late 1980s.
He earned bachelor’s and master’s degrees as well as a Ph.D. in engineering from Johns Hopkins University, in Baltimore.
(April 2022) 2022 Challenges to Security in SpaceAn Excerpt from the Executive Summary:
"Space is being increasingly militarized. Some nations have developed, tested, and deployed various satellites and some counterspace weapons. China and Russia are
developing new space systems to improve their military effectiveness and reduce any reliance on U.S. space systems such as the Global Positioning System (GPS). Beijing
and Moscow have also created separate space forces. As China’s and Russia’s space and counterspace capabilities increase, both nations are integrating space scenarios
into their military exercises. They continue to develop, test, and proliferate sophisticated antisatellite (ASAT) weapons to hold U.S. and allied space assets at risk. At
the same time, China and Russia are pursuing non-weaponization of space agreements in the United Nations.9 Russia regularly
expresses concern about space weapons and is pursuing legal, binding space arms control agreements to curb what it sees as U.S. strength in outer space.10,11 The expansion
of Chinese and Russian space and counterspace weapons combined with the general rise of other foreign space capabilities is driving many nations to formalize their space
policies to better position themselves to secure the space domain and facilitate their own space services."
READ MORE: https://www.dia.mil/Portals/110/Documents/News/Military_Power_Publications/Challenges_Security_Space_2022.pdf
(May 2022) The RNT Foundation has previously signed with the Open PNT Industry Alliance urging Congress to fund these important initiatives.
We join the alliance now in urging the Department of Transportation to contract for commercial
PNT services to meet the requirements of the law.
As we have said, before, though, the amount of money provided in the current fiscal year (which is more than half over) hardly seems enough for all
the studies and standards development the appropriation requires. We are concerned that there will be little, if any, left for actual services
that could make Americans safer. That is why we are encouraging members of Congress to make a larger appropriation for the fiscal year beginning
1 October of this year (2022).
Open PNT Industry Alliance advocates for alternative PNT in Appropriations Act
May 2, 2022 - By Tracy Cozzens
The Open PNT Industry Alliance (OPIA) issued a statement regarding the recently approved U.S. Fiscal Year 2022 Appropriations Act. The alliance advocates
for support of alternative positioning, navigation and timing
(PNT) services. In its statement, the 21 corporate members express support for the funding
provided to the Department of Transportation (DoT) to pursue alternative forms of
PNT.
READ MORE: https://www.gpsworld.com/open-pnt-industry-alliance-advocates-for-alternative-pnt-in-appropriations-act/
(May 2022) Blog Editor's (Dana) Note: Good to see the possibility of the US military adopting some of these improvements. Of course, we can't have an optimistic note without adding
some concerns:
We hope these upgrades survive the programmatic "valley of death" in which many (if not most) great capabilities developed during experimentation fail to get funded and
turned into real equipment warfighters use.
This project would be especially good if it was paired with a non-space-based capability since our adversaries have shown impressive abilities denying signals from space.
99.9% of GPS users are not in the military. What about them? Even if we are just worrying about military capability, what about all the civil users who support military
operations, training, maintaining, and equipage in some way as contractors, suppliers, etc.? - The
USA could use a more holistic approach to national security and strength.
NTS-3 Experiment Offers Possibility of Adopting GPS/PNT Protection In Existing Production Lines
By Frank Wolfe |
04/06/2022
Next March’s planned launch of the Air Force Research Laboratory’s
(AFRL) 1,100 pound experimental Navigation Technology Satellite-3
(NTS-3) offers the potential for the
U.S. Space Force to adopt advanced protection technologies for GPS and positioning,
navigation, and timing (PNT) systems, a U.S. Space Force official said on Apr. 6.
“We are watching NTS-3 very closely,” Cordell DeLaPeña, Space Systems
Command’s program executive officer of military communications and PNT, said during a press conference
at the Space Foundation’s Space Symposium in Colorado Springs, Colo. “I think that has high utility for incorporating high
TRL [technology readiness level], low-risk
capabilities into our existing production lines, as well as an opportunity to expand the architecture.”
READ MORE: https://www.defensedaily.com/nts-3-experiment-offers-possibility-of-adopting-gps-pnt-protection-in-existing-production-lines/space/
NASA,
new Navigation milestones, the Moon, and Mars!
Through
NASA’s Commercial Lunar Payload Services initiative, Firefly Aerospace of
Cedar Park, Texas, will deliver an experimental payload to the Moon’s Mare
Crisium basin. NASA’s Lunar GNSS Receiver Experiment (LuGRE) payload will test
a powerful new lunar navigation capability using Earth’s Global Navigation
Satellite System (GNSS) signals at the Moon for the first time. GNSS refers
to satellite constellations commonly used for position, navigation, and timing
services on Earth. GPS — the GNSS constellation operated by the U.S. Space
Force — is the one many Americans are familiar with and use on a daily basis.
(June 2022) The billon-dollar-a-day GPS mistake?:
May 25, 2022 - By Dana Goward
Est. reading time: 2 minutes
We all need to be careful that the numbers we are throwing around to support our case aren’t really undermining it.
Over the last several weeks, I have repeatedly heard government officials and others talking about the value of GPS to the U.S. economy.
In each case they cited a 2019 report sponsored by the National Institute of Standards and Technology. It determined that, if
GPS services were to go away, the U.S.
economy would lose one billion dollars a day.
A billion dollars is a lot of money.
Yet the U.S. annual gross domestic product is more than $22 trillion a year. That’s
more than $60B a day. One billion dollars is less than 1.7%.
That just doesn’t seem right!
.
GPS signals are critical for networks, transportation, communications, power grid operations, first responders…virtually every critical infrastructure. If they go
away, the U.S. GDP will certainly suffer much more loss than 1.7%. The economy would likely go from growing to shrinking and continue that way for quite a while.
I don’t know exactly how much the U.S. will suffer if GPS suddenly goes away, but I am sure it will be a lot. Texas alone
lost an estimated $195 billion with at least 57 dead
as a result of its February 2021 week-long power crisis. Although not caused by a GPS
outage, the number gives us real-world benchmarks for the impacts of a major tech
infrastructure failure.
If GPS fails, there will certainly be more accidents while people across the nation get used to it not being available. First responders will have a much harder time
getting places and using land mobile radios. All kinds of essential services will be disrupted. More people will die than would have been the case otherwise.
In December 2021, a member of the White House’s National Security Council said “GPS is still a single point of failure” for America.
That sounds like a pretty big hit to
the economy. Not to mention our national security.
In his book “Pinpoint – How GPS is Changing Technology, Culture and Our Minds,” author Greg Milner asks about the value of GPS. His answer is another question. “What’s
the value of oxygen?”
The authors of the NIST-sponsored study were undoubtedly diligent. But they were faced with an impossible task – to quantify the unquantifiable. And like any analysis,
they were limited in what they could do by the available time, money, and hard data. They were asked for a number. They delivered one that could be easily supported.
A billion dollars is a lot of money. It might be a fairly impressive sound bite for general audiences.
Government budget analysts and policy makers, though, are accustomed to dealing with dollars in the hundreds of billions and trillions.
A billion a day, while not
chump change, is not a major issue.
Protecting GPS and ensuring the nation has resilient positioning, navigation and timing services are major issues.
We all need to be careful that the numbers we are throwing around to support our case aren’t really undermining it.
(June
2022) NASA, new Navigation milestones, the Moon, and Mars!:
Through
NASA’s Commercial Lunar Payload Services initiative, Firefly Aerospace of
Cedar Park, Texas, will deliver an experimental payload to the Moon’s Mare
Crisium basin. NASA’s Lunar GNSS Receiver Experiment (LuGRE) payload will test
a powerful new lunar navigation capability using Earth’s Global Navigation
Satellite System (GNSS) signals at the Moon for the first time. GNSS refers
to satellite constellations commonly used for position, navigation, and timing
services on Earth. GPS — the GNSS constellation operated by the U.S. Space
Force — is the one many Americans are familiar with and use on a daily basis.
(June 2022) Blog Editor's Note: Some really neat stuff in to day's email from the Secure World Foundation:
One of them is a set of fact sheets on ASATs that are great reference material. Also useful if you have trouble
staying awake late at night.
And there is a nifty info graphic about ASATs (thumbnail below) that you can access as a hi-res file here.
SWF Releases 2022 Fact Sheets on Anti-Satellite Testing, Military and Intelligence RPOs, and the X-37B
Tuesday, May 31, 2022
The continued proliferation counterspace capabilities and resurgence of anti-satellite
(ASAT) testing in space and growth in robotic rendezvous
and proximity operations (RPOs) conducted for military and intelligence purposes have generated concerns from many countries about the increasingly
contested nature of space. While many RPO activities are not directly aggressive
nor destructive themselves, they can lead to misconceptions or
heightened tensions that could negatively impact space security and stability. Additionally, destructive
ASAT tests have created thousands of pieces
of orbital debris over the last several decades, which can pose long-term risks to all space activities.
https://swfound.org/news/all-news/2022/05/swf-releases-2022-fact-sheets-on-anti-satellite-testing-military-and-intelligence-rpos-and-the-x-37b?mc_cid=75034a6c46&mc_eid=4aaa2d2d27
(Apr. 2021) Would Russia Invade Ukraine and China Invade Taiwan Simultaneously? - 19FortyFive:
"To avoid even the possibility of stumbling into such a horrific dilemma, the United States needs to urgently reform how it engages with the rest of the world. The reality
is that the U.S. military genuinely is the strongest in the world right now (though both Russia and China have made significant strides in modernizing their forces) and
can deter any nation – China and Russia included – from launching an unprovoked attack against our country. But we must concurrently recognize that our military is
not invincible, capable of imposing our will on all nations of the world, simultaneously."
https://www.19fortyfive.com/2021/04/would-russia-invade-ukraine-and-china-invade-taiwan-simultaneously/
(Apr. 2021) New Tactical ISR Satellites Provide Global, Persistent Support for
Warfighters:
The LM 400-based tactical ISR satellites will play a key role in
Joint All-Domain Command and Control (JADC2) by allowing tactical warfighters to better employ
space-based capabilities. #LockheedMartin is also developing and building 10 #space vehicles over the next two years for the
Space Development Agency’s
Transport Layer Tranche 0, cited as the backbone of JADC2, enabling even more connectivity between
ISR and #warfighters.
https://news.lockheedmartin.com/tactical-isr-satellites?_lrsc=a10e50af-26f7-488d-b825-ee61be3924b8
(Apr. 2021) DARPA chooses three firms to design nuclear-powered space vehicle:
Defense Advanced Research Projects Agency (DARPA) has picked three companies
to design a nuclear thermal propulsion system that will operate above
low Earth orbit in
2025, the U.S. agency announced April 12.
General Atomics, BLUE ORIGIN and Lockheed Martin received
contract awards and will be the prime contractors for the first phase of the
Demonstration
Rocket for Agile Cislunar Operations, or DRACO, program.
DARPA believes nuclear-powered propulsion could enable rapid maneuver in space — a capability that is difficult to achieve with current electric and chemical
propulsion systems.
(Apr. 2021) Assured PNT Summit - Opening Remarks:
Defense Strategies Institute Assured PNT Summit
Moderator: Dana A. Goward
Opening Comments, 14 April 2021:
Good morning! So good to see everyone and be here on behalf of the RNT
Foundation. We are a scientific and educational charity. As such, we endorse no products
or services but are pleased to be cooperating with DSI on this effort and appreciate the program’s commercial sponsors.
Thanks to all!
This event is closed to the media and there will be no recordings. All comments are not for attribution, the
“Chatham House Rules.” We are looking for a free
and open exchange of ideas from everyone.
One exception that I will make is that you are free, and encouraged, to quote and attribute anything I say.
All we do at the RNT Foundation is open source and
publicly releasable as part of our educational efforts.
Assured PNT:
Air Force U-2 pilots purchase Garmin watches and navigate using Glonass and
BeiDou to conduct their surveillance missions because the GPS jamming is so
bad.
Thousands of ships, well offshore in the Black Sea, incorrectly report
that they are moored in the middle of inland Russian airports.
Hundreds of ships and fitness users in China and Iran report
they are far from their true location and traveling in counterclockwise
circles.
Civil drones lose GPS signals and crash into houses.
A commercial airliner nearly impacts a mountain because of GPS interference.
NATO Exercises in Norway and elsewhere are jammed by transmitters in the Russian homeland.
Criminals routinely use jamming and spoofing to steal cargo and evade police.
And our sun is always lurking in the background with the threat of a major event that could keep GPS signals from getting through for
days, or even a
Carrington event that will immediately destroy half the satellites, then others as they come into view.
Assured PNT – everybody wants it, nobody has it. At least NOT in the U.S.!
In 2016, Iran announced they had created a terrestrial navigation and timing system that makes them independent from space.
Saudi Arabia has a similar system.
South Korea has gone one step further by modernizing their terrestrial system and integrating it in a system-of-systems approach with GNSS and
maritime R-mode
VDES.
Russia and the Commonwealth of Independent States republished their radio-navigation plan last year saying they are retaining and upgrading their
terrestrial
Chayka system so as to not be dependent upon space-based navigation and timing. There is also an indication that
Russia may have an expeditionary
version of this system for its forces to take into battle.
China has the most resilient Assured PNT structure and plan, though.
At 2019’s Stanford PNT symposium, they announced their plan for “comprehensive”
PNT. One involving satellites at GEO, MEO, and LEO, expanding their Loran system to cover the entire
country, upgrading it to eLoran, developing WiFi and
5G-based timing and navigation, and expanding research on interials(?) and
clocks. Everything we have seen since then leads us to believe that they are
executing this plan. China seems to believe in and be dedicated to the idea of Assured PNT.
While we talk a lot about assured PNT in the United States and the West, we have done little. And so,
we have lost the global PNT conflict in all three
phases of war: tactical, operational, and
strategic!
Our tactical disadvantages are made clear every day, especially in the middle east and
other conflict and operating areas. Just last week, for example,
Russia or its proxies restarted jamming operations in eastern Ukraine as a part of the Russian troop buildup on the border. As a result, the
Organization
for Security Cooperation in Europe has been unable to use its long-range UAVs to monitor compliance with the Minsk Protocols.
The U.S. and the west have been hampered at the operational level of war as
well. Our adversaries have (already) shaped the battle spaces around the
world with jamming and spoofing forcing us to accommodate to the conditions they have created. We should be shaping it to our advantage and
making them adapt.
And we are certainly at a strategic disadvantage when our adversaries can directly or through a proxy strike a devastating blow to our homeland by
interfering with GPS, while a similar action on our part would have much less (of
an adverse) effect on them.
We are dangerously behind where we need to be. This (situation) has not been lost on Congress, which has
mandated improvements in Assured PNT for
both military and civil applications, although, despite deadlines, those improvements have yet to come about.
I hope that today and tomorrow we will find out about how America is going to
catch-up and, perhaps, even regain the lead in the undeclared global PNT war.
We have a very impressive list of topics and speakers for you today and tomorrow. This is a unique opportunity for you to interact with them, so we want to
encourage a free & open exchange under our "Chatham House
rules". Please ask questions, engage the speakers and take advantage of this opportunity.
As you listen to their presentations, you might want to think about how they are addressing the holistic approach to assured PNT that my colleagues and I at
the National PNT Advisory Board have adopted – Protect, Toughen
(robustify), and Augment.
Protect the satellites and signals, Toughen users and their
equipment, and Augment GPS/GNSS signals with alternative PNT
sources.
(October 2021) Nuclear Missile Submarine Chart:
https://www.popularmechanics.com/military/navy-ships/a21204892/nuclear-missile-submarines-chart/
(October 2021) Some Computers Could Crash Sunday Due to A Bug in Getting GPS Derived Time -
ZDNet:
Blog Editor's Notes: Really, really interesting piece about the importance of time that also shows the dangers of getting time from only one source.
We think it would be a great idea if Americans, like folks in China, Russia, and South Korea, could get authoritative time from the government via
multiple diverse sources.
If you haven't yet read, check out our white paper "A Resilient National Timing Architecture."
BTW - we changed the title of this post from what ZDNet had to make it a little bit clearer what the article was about.
Thanks to a nasty GPSD bug, real-life time travel trouble arrives this weekend.
On October 24, 2021, some time-keeping systems are going to take a trip back in time to March 2012, unless you update your GPSD programs.
By Steven J. Vaughan-Nichols for Networking | October 19, 2021 | Topic: Networking
"Does anybody really know what time it is? Does anybody really care?"
Actually, if you use computers for pretty much anything, you do. Oh, you may not know it if you're not a system or network administrator, but security,
identification, networks, everything that makes the internet go depends on accurate time-keeping. Some systems rely on Global Positioning Systems (GPS)
appliances and the GPSD daemon to tell the exact time, and a nasty bug's been uncovered in GPSD that's going to pop up on October 24, 2021. If left
unpatched, it's going to switch your time to some time in March 2012, and your system will crash with a resounding
kaboom! Here's how it works.
READ MORE: https://www-zdnet-com.cdn.ampproject.org/c/s/www.zdnet.com/google-amp/article/thanks-to-a-nasty-gpsd-bug-real-life-time-travel-trouble-arrives-this-weekend/
(October 2021) Fighting Evolving Threats: Meet The MAPS GEN I APNT System:
https://www.youtube.com/watch?v=OWVwgcwFjz0
(October 2021) TrustPoint raises $2 million for GPS alternative - Space News:
Blog Editor's Note: In-space alternatives to GPS/GNSS are proliferating. Trustpoint is surging forward, per the below article, and Xona is getting ready
to put a demo satellite in orbit (full disclosure, Xona is an RNTF corporate
member). Satelles is already offering time and location services. OneWeb is
projecting PNT capability in its Phase 2, and folks are already inferring location from Starlink.
They all are successfully dealing with a combination of rocket science, advance physics requiring Einstein's general and special theories of relativity,
and very sophisticated clock and RF technology. So it is clear the engineering challenges can be overcome.
What is less clear is how successful the business cases will be. Low earth orbit allows for greater precision and higher power (more difficult to disrupt)
signals,than is possible with GNSS at medium earth orbit. And new builds can overcome many challenges that have faced
GNSS over the last 20 years with
improved technology to encrypt, perhaps authenticate, and otherwise better protect signals.
But will these advantages be enough to successfully compete with the combined power of free signals from four GNSS constellations?
It is certainly in the nation's interest that one or more of these systems becomes viable. We wonder if and how the government will support this national
interest. Or will it sit by and "let the market decide"? This would include the potential outcome that the market is happy to continue relying on free
GPS/GNSS and accepting the risk of the entire house of cards falling due to a coronal mass ejection or some other adverse space-based event.
TrustPoint raises $2 million for GPS alternative
by Debra Werner — October 18, 2021
SAN FRANCISCO – TrustPoint Inc., a startup developing a global navigation satellite system (GNSS), has raised $2 million in seed funding from venture
capital firm DCVC.
With the funding announced Oct. 18, TrustPoint plans to expand its engineering team, continue developing core technologies, including satellite payload
testing, and extend key partnerships.
Heavy global reliance on GPS, Europe’s Galileo, Russia’s Glonass and
China’s Beidou for everything from communications and transaction timing to maritime
and aircraft navigation is prompting companies and government agencies to look for backups and alternatives.
TrustPoint founders Patrick Shannon, a former Astro Digital vice president, and
Chris DeMay, former Hawkeye 360 founder and chief technology officer, said
GPS alternatives are necessary because the current system is inaccurate, slow, unencrypted, and susceptible to jamming and spoofing. What’s more,
GNSS
systems alone are not precise enough for many of the emerging commercial applications like drone delivery, self-driving cars, urban air transportation and
augmented reality, Shannon and DeMay said.
READ MORE: https://spacenews.com/trustpoint-seed-round/
(Apr. 2021) What Technologies Can Secure GPS? - Webinar w/Civil PNT Leaders fm 3 Administrations:
Blog Editor's Note: This WILL be interesting. Hosted and moderated by Scott Pace (GWU Space Policy Institute, Exec Dir of Space Council in the last administration),
it will feature Greg Winfree, Diana Furchtgott-Roth, and Dr. Robert Hampshire.
Greg & Diana (both RNT Foundation members!) were the leads at DoT Research and Technology in the
Obama and Trump administrations, and therefore the
leaders for civil PNT policy in the federal government. Dr. Hampshire is filling that role in the Biden administration.
This is a free event but you do have to register in advance.
From the event page on Eventbrite:
What Technologies Can Secure GPS?
Join us for a discussion of the Department of Transportation's Complementary PNT and GPS Backup Technologies Demonstration
Report.
About this Event
Three separate laws have required the U.S. Department of Transportation (DOT) to back up and complement the Global Positioning System, subject to congressional
appropriations. To provide a roadmap, in January 2021, the Department released its Complementary PNT and GPS Backup Technologies Demonstration
Report.
During this webinar, Acting Assistant Secretary Robert Hampshire will offer introductory remarks and
DOT's Karen Van Dyke and Andrew Hansen will follow up
with a presentation of the report. George Washington University Adjunct Professor Diana Furchtgott-Roth and the
Texas Transportation Institute's Greg
Winfree will provide comments.
A public Q&A will follow the discussion. The program will open with remarks from Scott Pace, director of the Space Policy
Institute, who will also moderate
the discussion.
Date And Time
5 May 2021
2:00 PM - 3:30 PM ET
REGISTER HERE: https://www.eventbrite.com/e/what-technologies-can-secure-gps-tickets-150834212189
(Mar. 2021) Big New Interceptor Deal Part Of Biden Missile Defense Push:
The Biden administration is pushing ahead with multiple missile defense initiatives
in its first 100 days, a sign the Pentagon will make new investments in
the capability to meet developing Chinese, North Korean and Russian
capabilities.
https://breakingdefense.com/2021/03/big-new-missile-defense-contract-comes-as-part-of-larger-defensive-push/?_lrsc=93a1c165-40c5-4a13-8b9b-3ac041314b8c
(Apr. 2021) Next-gen intercontinental ballistic missile interceptor estimated to cost nearly $18 billion:
The Pentagon’s Next-Generation Interceptor that is being competitively developed to replace the current ground-based interceptors within the United States’
homeland intercontinental ballistic missile defense system is estimated to cost nearly
$18 billion across the life of the program.
An independent cost estimate from the Defense Department’s Cost Assessment and
Program Evaluation (CAPE) office — first reported by Bloomberg and since
obtained by Defense News — has determined the total cost to develop the NGI will come to roughly
$13 billion while procurement as well as operation and
sustainment will come to a little over $2 billion each.
The Pentagon announced in August 2019 its intention to build a new NGI after the
Redesigned Kill Vehicle (RKV) program — that would upgrade the
Ground-Based
Interceptors (GBI) with the ability to go after more complex threats more reliably — was abruptly killed.
#pentagon #defense #defence #defenseindustry #defenceindustry
(Apr. 2021) OneWeb PNT Possibilities:
Blog Editor's (Dana A. Goward) Note: Some buzz last week on this due to public comments made by the
OneWeb CEO, Neil Masterson:
There are several ways OneWeb could be used for . Future satellites could be modified for the purpose, future payloads could carry purpose-built satellites, and
PNT could be inferred from the thousands of communications satellites forecast in the constellation. All are possibilities. All have costs and technical challenges.
Or, there could be no PNT functionality at all.
Here are a couple of reports pertaining to Masterson's comments:
OneWeb may demonstrate a navigation payload later this year, CEO Neil Masterson said today at the Satellite 2021 LEO Digital Forum. OneWeb could offer a
"real alternative" to Galileo with its second-generation satellites, which are scheduled to enter service in 2024, but may provide "good enough"
precision navigation
and timing (PNT) before that.
The U.K. is seeking alternatives to Galileo's secure navigation signal since it is no longer part of the European Union. After
initially considering building its own PNT constellation, the U.K. announced plans last year to consider commercial alternatives including one proposed by
OneWeb.
Since PNT has become a cornerstone of economic and military activity, governments around the world are looking for ways to augment or reinforce
PNT services. The
U.S. government identified "suitable, mature and commercially available technologies to backup or complement the timing services provided by GPS," in a
Transportation Department report released in January 2021. Due to varied
PNT use cases, however, no single PNT system can take the place of
GPS. Instead,
the report recommends adoption of "a diverse universe of positioning and navigation technologies."
http://interactive.satellitetoday.com/via/leo-digital-forum-show-daily/oneweb-ceo-neil-masterson-talks-telcos-and-terminals/
(Apr. 2021) Russia ramps up GPS jamming along with troops at Ukraine border - GPS World:
https://www.gpsworld.com/russia-ramps-up-gps-jamming-along-with-troops-at-ukraine-border/
April 21, 2021 - By Dana A. Goward
Two recent reports from the Organization for Security and Co-operation in
Europe (OSCE) have described a recent increase in GPS jamming, presumably by Russian
or pro-Russian forces in Ukraine. This comes as Russia has increased its troop numbers and activity along its border with Ukraine.
OSCE is charged with a Special Monitoring Mission (SMM) in Ukraine which observes and reports on how well both sides are adhering to the
Minsk Protocol agreement.
The agreement was signed in September 2014 by participants in the conflict in an effort to end open hostilities.
One of the ways the OSCE mission monitors activity and compliance in the region is with
long range UAVs. As early as November 2014, the organization reported
UAV operations being thwarted by interference with GPS signals.
Two recent OSCE spot reports have highlighted a resurgence in
jamming.
An 7 April 2021 report described interference that prevented a UAV takeoff the previous
day. While the organization’s UAVs had been experiencing increased
interference since March 2021, this was the first time since October 2014 that
it had thwarted a mission before takeoff.
The report also documented an increasing level of jamming activity.
“Over the last two months, 62.5 percent of SMM long-range UAV flights encountered GPS signal interference and on
75 percent of the affected flights it occurred
more than once.”
A second report on 9 April 2021 outlined continuing problems that caused missions to be aborted. It emphasized that
this was a violation of the agreement
signed by all parties and greatly hampered OSCE’s mission.
“Any GPS signal interference hinders the Mission’s ability to conduct effective monitoring and reporting of the security situation in line with its mandate.
Long-range UAVs are an essential part of SMM operations, especially at night and in areas where the Mission’s monitoring and freedom of movement are restricted.”
GPS jamming and spoofing are important parts of Russia’s arsenal to counter any technological advantage the west may have over their forces. A 2015
Sputnik article bragged their electronic warfare kept U.S. cruise missiles from hitting their targets at the start of the 2003 invasion of
Iraq. Also, that this advanced
capability “renders aircraft carriers useless.”
Interference with GPS signals is a regular feature of Russian military and internal security operations.
Upon more than one occasion, Russia has jammed GPS signals near NATO exercises and regularly jams broad areas in the Middle East from a base in
Syria.
Its spoofing of GPS signals in Moscow and the Black Sea to cause receivers to report that they are at airports kilometers away from their true location
has been well documented.
The United States has formally expressed concerns about the recent increase in the number of Russian troops and their activity at the Ukrainian border. It has been
reported that two U.S. Navy ships are on their way to the Black Sea to help monitor the situation.
Dana A. Goward is president of the Resilient Navigation and Timing
Foundation.
(Apr. 2021) https://machinelearningmastery.com/gradient-in-machine-learning/
(Apr. 2021) The Need for Resilient PNT Has Never Been Greater - EE Times:
Blog Editor's Note: A very good summary article by Guy Buesnel, a long time RNT Foundation supporter and member of our International Advisory Committee.
For more information on the system-of-systems approach he describes in the article,
we recommend the very thorough MarRINav report sponsored by the
European Space Agency and led by our friends at NLA International.
The Need for Resilient PNT Has Never Been Greater
By Guy Buesnel, Spirent Communications 04.22.2021
Real-world instances of Global Navigation Satellite System jamming and spoofing have been steadily increasing in recent years. Those incidents include
hundreds of commercial ships being spoofed in the Black Sea and repeated GNSS jamming affecting commercial aviation in Norway.
Air traffic manager Eurocontrol recently disclosed more than 3,500 instances of
GPS jamming were reported by pilots during 2019 alone.
Elsewhere, the U.S. Federal Communications Commission has conditionally approved an application by satellite communications provider
Ligado Networks to
deploy a low-power terrestrial nationwide network in the L-Band to support 5G and Internet of Things
services. The decision means that GNSS systems and
devices must be capable of resisting adjacent-band radio frequency interference at extremely high-power levels while
still providing extremely accurate
and precise data to users.
Over-dependence on GPS and other navigation aids along with growing vulnerabilities including jamming, spoofing and other forms of interference highlight
the need for terrestrial backups to current GNSS systems. We take a hard look at the scope of the problem and possible remedies in our upcoming
GPS Special
Project.
READ MORE: https://www.eetimes.com/the-need-for-resilient-pnt-has-never-been-greater/#
(Apr. 2021) The Intelligence Community's Deadly Bias Toward Classified Sources:
by Cortney Weinbaum
April 12, 2021
For years, government officials, commissions, and think tanks have warned that the U.S. intelligence community has blinded itself to enormous sources of
intelligence, simply because the information is publicly available. In other words, the intelligence community would prefer to rely on billion-dollar
classified satellites and intelligence-collection programs rather than to gather unclassified information on the internet for free.
Examples are rife. Russia conducted a strategic misinformation campaign to influence the results of elections in multiple countries, including the UK,
Ukraine (PDF), France, and, eventually, the United States (PDF), and they did it on social media in view of
everyone, except the intelligence officers who
only look at classified sources. Despite the signals that were available, U.S. elected officials (PDF) described not being adequately warned.…
The remainder of this commentary is available at defenseone.com.
(Mar. 2021) Space Debris Threatens GNSS:
Blog Editor's Note: The greatest threat from space debris is unquestionably at LEO. Many in the
PNT community have considered GPS, Galileo, and other GNSS at
MEO relatively safe from debris. It seems "that ain't necessarily
so".
Papers on debris at MEO are difficult to come by. We did find one from an
ESA conference that found collisions at LEO were responsible for much of the debris
at MEO.
The recently developed Aerospace Debris Environment Projection Tool was used to project the future debris environment in
medium Earth orbit (MEO) over the
next 200 years. The entire Earth orbital population was modeled to account for the possibility of cross-coupling between the MEO population and the low Earth
orbit (LEO) and geosynchronous populations via objects on highly eccentric orbits that transit through
MEO. It was found that a large fraction of the MEO debris
originated from collisions in LEO involving satellites and rocket bodies that transit through LEO and
MEO.
Another paper pointed out that too much debris at LEO could make it difficult to transit the zone safely and put satellites in MEO and
GEO in jeaprody.
The incident reported below is likely not the first time a GNSS satellite
has been threatened by space debris. It does serve as an alert, though, reminding
us to not be complacent about any potential threat to these systems that are so essential to so many technologies and services.
Galileo satellite performs collision avoidance maneuver:
March 25, 2021 - By Tracy Cozzens
In a first for Galileo, a satellite performed a collision-avoidance maneuver to avoid space debris.
Under the management of the European GNSS Agency (GSA), the maneuver for satellite
GSAT0219 was performed 6 March 2021 following a collision risk alert received
from EU Space Surveillance and Tracking (EUSST).
READ MORE:
https://www.gpsworld.com/galileo-satellite-performs-collision-avoidance-maneuver/#:~:text=In%20a%20first%20for%20Galileo,maneuver%20to%20avoid%20space%20debris.&text=On%20Feb.%2025%2C%20the%20Galileo,upper%20stage%20launched%20in%201989.
(Mar. 2021) Aviation Groups Petition Govt over Deliberate GPS Jamming:
Blog Editor's Note: Aviation is somewhat unique among modes of transportation as it has an alternate PNT system for when GPS is not available. It is a network
of short range terrestrial beacons of VORs, DMEs, and TACANs
(TACAN is military only). See graphic courtesy of Mitch Narins, Strategic Synergies, LLC.
As one example, we reported three years ago about concerns formally expressed by the
Radio Technical Commission, Aviation.
Recently an IEEE article revealed the FAA has a wealth of data showing that such disruptions are exceptionally
common.
The letters below make it fairly clear the government has failed to adequately address these concerns.
There are undoubtedly several reasons for these on-going problems.
One is that, apparently, the FAA and DOD have not been willing to engage with the community on this issue.
Another is that, on the aircraft side, the FAA authorizes many small aircraft to operate without formal electronic navigation capability. They ostensibly
find their way by visual references (looking at the ground for
landmarks, following roads, etc). However, most do have a non-certified "situational awareness"
GPS receiver, not really authorized by the FAA for navigation, but undoubtedly used as such.
When GPS is deliberately jammed these aircraft are put at even
greater risk than others.
Also, many better equipped aircraft that do have VOR and DME capability, do not have navigation systems that integrate the information from these beacons to
allow point-to-point navigation (a capability call "area navigation," or
RNAV). So when GPS is not available, these aircraft must fly longer and less
efficient routes between beacon waypoints.
These on-going challenges in aviation provide lessons for future alternate PNT systems. Not only must the alternate system provide sufficient coverage and
availability, it must also be widely adopted by users and integrated into their systems for it to be effective. Government has a number of tools available
to make this happen. When it fails to use all those tools, the alternate system is much less effective in protecting the public, and on-going problems
occur.
---
We should also note that despite the FAA touting the VOR/DME/TACAN system as
its alternative to GPS, the agency has failed to recapitalize the network, along
with Instrument Landing Systems (ILS) at airports.
Much of the equipment in use is well beyond its service life. And we are told that, while the
FAA has some minimal VOR and DME replacement equipment on hand,
it failed to budget for installation. So a lot of the new equipment tends to sit in government warehouses collecting dust.
And while new, more effective and efficient ILS equipment is available, it has not been
acquired. We are told that this poses a safety problem for landing
aircraft, and foregoes an approximate 20% increase in airport efficiency that has been realized by other nations.
All told, quite a few reasons the aviation community is unhappy with the FAA's approach to navigation.
NBAA, AOPA Call Upon Agencies to Mitigate Impact of Intentional GPS Interference.
Contact: Dan Hubbard, 202-783-9360, dhubbard@nbaa.org
Washington, DC, March 5, 2021 – The National Business Aviation
Association (NBAA) and the Aircraft Owners and Pilots
Association (AOPA), in a letter to the
Federal Aviation Administration (FAA) and Department
of Defense (DOD), expressed concern about restrictions to airspace and airports caused by the
intentional
jamming of GPS and are seeking mitigations on the operational impact of these interference events.
In a letter to the FAA and DOD, the organizations recognized the importance of
DOD’s mission and the agency’s need to simulate the loss of GPS as part of its
effort to defend and maintain the global navigation system. However, as NBAA and AOPA noted, the National Airspace System (NAS) has become increasingly reliant
on GPS as the primary source of navigation and aircraft system functionality, while reducing reliance on ground-based navigational infrastructure.
“Despite reduced operations in the NAS over the past year, general aviation continues to show increased activity and volume, exceeding commercial airline
operations,” the letter states. “In recent months, operators have continued to report operational impacts and reduced access to airspace and airports
resulting from intentional GPS jamming events.”
Read NBAA’s and AOPA’s full letter to the FAA and DOD.
(pdf)
The associations’ letter also noted the aviation community had NOT received a response from the
FAA or DOD to a 2018 RTCA report on the operational impacts
of intentional GPS interference, which included more than two dozen detailed recommendations to limit the operational impact of these events on civilian air
traffic.
During the RTCA deliberations, the FAA and DOD acknowledged that the frequency and impact of these intentional jamming events grew significantly over the
preceding decade and would continue to escalate, the trade groups added.
“The growing reliance on GPS in the National Airspace System, combined with the
increasing frequency of intentional GPS jamming events, makes it imperative
that the FAA and the DOD have mitigations in place to ensure the safety and reliability of the
NAS during these events,” said Heidi Williams, NBAA director,
air traffic services and infrastructure. “We look forward to working with the agencies to employ the
RTCA report’s recommendations and ensure our national
security and the safety and efficiency of the NAS.” “It is vital that pilots have continuity and access to optimal navigational and safety tools, of which
GPS is vital,” said Jim Coon, AOPA senior vice president of government affairs and
advocacy. “We strongly support our warfighters, but we believe DOD and
FAA should review their GPS testing processes so that our nation’s airspace continues to be as safe as possible.”
LINK:
https://nbaa.org/press-releases/nbaa-aopa-call-upon-agencies-to-mitigate-impact-of-intentional-gps-interference/
(Mar. 2021) Protect your PNT with GPS Ant-Jam Technology from Hexagon |
NovAtel:
GNSS technology establishes your Position, Navigation, and
Time (PNT) in the environment -- but we have to protect it.
Defend your PNT in challenging environments through Hexagon | NovAtel anti-jam antennas, interference mitigation and
GNSS+INS combined systems.
Read more about how to protect the integrity of your APNT solution >> https://hxgn.biz/3u8HCY3
(Mar. 2021) This morning the Prime Minister of Australia Scott Morrison officially unveiled our Australian Space Discovery Centre to the public!:
The Prime Minister was joined by the Premier of South Australia, Steven
Marshall, Australian Space Agency Head, Enrico Palermo, Australian Space Agency
Advisory Board Chair, Dr. Megan Clark, and Australia’s Chief Scientist, Cathy
Foley.
The Australian Space Discovery centre is based at Lot Fourteen in Adelaide, South Australia and officially opens in
May (2021)!
Find out more and pre-book your experience here: https://bit.ly/3r7zZjZ
(Mar. 2021) Our BookEnd column in March's MWJournal features "Introduction to LabVIEW FPGA for RF, Radar, and Electronic Warfare Applications."
Topics include best practices for multi-FPGA solutions and guidance for high throughput,
low latency FPGA-based RF systems.
https://www.microwavejournal.com/articles/35620-bookend
(Mar. 2021) Next 10 years of EGNOS to focus on drones:
https://www.gpsworld.com/next-10-years-of-egnos-to-focus-on-drones/
Air Force Wants Lasers on Fighter Jets by 2025:
Lockheed Martin is working toward outfitting a directed energy system on fighter jets by the middle of the decade. To build and manufacture the systems,
we are investing more than $20 million into our Orlando-based optical components center.
https://www.nationaldefensemagazine.org/articles/2020/11/9/air-force-wants-lasers-on-fighter-jets-by-2025?_lrsc=8b352be7-eb13-4a11-a239-303b3d163bf4
How The Once Elusive Dream Of Laser Weapons Suddenly Became A Reality:
A good piece below on how industrial applications have helped make military lasers
a reality for small scale applications (and why Star Wars is still a pipe
dream):
https://www.thedrive.com/the-war-zone/37775/how-the-once-elusive-dream-of-laser-weapons-suddenly-became-a-reality
Laser Weapons On The Battlefield Of Tomorrow: Separating Fact From Fiction:
https://www.thedrive.com/the-war-zone/37646/laser-weapons-separating-fact-from-fiction
FLIR Systems Acquires Altavian, Inc.:
FLIR Systems Acquires Altavian, Inc. https://bit.ly/2VsKtvS
https://www.flir.com/news-center/corporate-news/flir-systems-acquires-altavian-inc/?utm_content=1606915967&utm_medium=social&utm_source=linkedin
Raytheon Technologies to Buy Smallsat Maker Blue Canyon; Roy Azevedo Quoted:
https://www.govconwire.com/2020/11/raytheon-technologies-to-buy-smallsat-maker-blue-canyon-roy-azevedo-quoted/
Cheap GPS jammers a major threat to drones - ZD Net:
The article mentions interference with a display involving hundreds of drones. There have been other incidents, of course, in China and elsewhere. One example is the
UK accident we reported on that could have resulted in a fatality, according to the government's investigation report.
We agree with the below article that GPS/GNSS receivers should include better hardware and software to make them more resilient to jamming and spoofing.
That's only part of the solution, though. A holistic approach is needed if
GPS/GNSS is to be managed property. We agree with the "Protect, Toughen, and Augment" scheme advocated by the
National Space-based Positioning, Navigation, and Timing Advisory Board.
Jammers that can be bought for as little as $50 threaten commercial drones, but there are options.
With rotors whirring and airframes hurling through the air, drones can be very dangerous when flights don't go as planned. There's been
much teeth gnashing over the FAA's measured approach to commercial drone policy adoption, but the fact is there are real dangers, including from bad actors using inexpensive
GPS jammers.
GPS signal jamming technology is evolving, decreasing in size and cost. Today, jammers can be bought online for as low as $50. Long a threat to military assets, jamming is now a commercial concern as commercial drone deliveries become a reality, and attacks are becoming pervasive globally. This threat now affects commercial, law enforcement, and defense drones on critical missions.
https://www.zdnet.com/article/cheap-gps-jammers-endanger-drones/
Drone Warfare:
https://www.youtube.com/channel/UCCukeofUEYHvnEK4syqJbcA
China expanding Loran as GNSS backup - GPS World:
https://www.gpsworld.com/china-expanding-loran-as-gnss-backup/
https://www.gpsworld.com/china-leads-world-with-plan-for-comprehensive-pnt/
Directions 2021: BDS marches to new era of global services - GPS World:
Earlier this year, BDS-3, the global version of the BeiDou Navigation Satellite System
(BDS), was formally commissioned, marking the completion of its three-step development process. Read about the system's services and accomplishments.
https://www.gpsworld.com/directions-2021-bds-marches-to-new-era-of-global-services/
South Korea discusses decision to combine GPS and eLoran - Geospatial World:
https://www.geospatialworld.net/blogs/south-korea-discusses-decision-to-combine-gps-and-eloran/
Novatel:
What is mobile mapping?
https://novatel.com/industries/mobile-mapping
Learn about how #GNSS antennas and receivers are combined with Inertial Navigation Systems to provide highly accurate data on the positioning, velocity and attitude of moving objects, and how engineers use these devices to document landscapes and more >>
https://hxgn.biz/2Vkj7aM
Next Generation Interceptor: Never Fail Defense Against Evolving Threats:
The Next Generation Interceptor program is focused on strengthening first-line defenses against advanced emerging missile threats.
This challenge is not one to be taken lightly – and we're throwing the weight of the
Lockheed Martin enterprise behind our proposed solution. We're developing a cutting-edge offering based on our expertise from other strategic defense systems, like
Terminal High Altitude Area Defense and hypersonic strike systems. And we're counting on more than our proven systems – we're also focused on designing for the future. We're leveraging the best technologies and smart tools for this mission, relying heavily on digital engineering,
DevSecOps and other tech like AI and machine learning.
Learn more about the need for NGI, and how we plan to deliver for our
warfighters: https://www.lockheedmartin.com/en-us/capabilities/space/space-missile-defense.html
IMPORTANT
Acquisition of AGI Extends the Digital Thread Throughout the Mission |
Ansys Blog
https://www.ansys.com/blog/acquisition-of-agi-extends-the-digital-thread
Raytheon awarded $235.6M for production of Silent Knight Radar:
https://www.upi.com/Defense-News/2020/12/01/Raytheon-awarded-2356M-for-production-of-Silent-Knight-Radar/3121606871049/
China's Version of GPS is Better, Says US Satellite Receiver Company:
Re: fake news about Beidou: the nominal number of MEO satellites is the same
(24) for both GPS and Beidou. The GEO and IGSO satellites of the Beidou constellation
are useful only above China.
I am not surprised that Galileo and Beidou may have a somehow better performance than
GPS, but, quoting Bernard of Chartres, we should not forget that: "We are dwarfs standing on the shoulders of
giants".
https://radiichina.com/china-beidou-gps/
Many thanks to Black Dot GNSS and Simon Banville for digging a little deeper into the data behind our "RTK From the Sky" white paper.
We'll be participating in a webinar this month and sharing further technical details behind instantaneous cm-level #PPP corrections, stay tuned!
https://lnkd.in/gBc8PTJ
#GNSS #Webinar
https://www.blackdotgnss.com/2020/11/30/rtk-from-the-sky/
Science: Death by "Spaghettification": Scientists Record Last Moments of Star Devoured by a Black Hole:
The phenomenon, known as a tidal disruption event, is the closest flare of its kind yet recorded, occurring just 215 million light-years from Earth.
https://www.linkedin.com/pulse/death-spaghettification-scientists-record-last-star-lieberman-/?trackingId=fP4Tu6fzvInYkaVA3fy6rw%3D%3D
The phenomenon, known as a tidal disruption event, is the closest flare of its kind yet recorded, occurring just 215 million light-years from Earth. It is caused when a star passes too close to a black hole and the extreme gravitational pull from the black hole shreds the star into thin streams of material – a process called ‘spaghettification’. During this process some of the material falls into the black hole, releasing a bright flare of energy which astronomers can detect.
https://www.birmingham.ac.uk/news/latest/2020/death-by-spaghettification-scientists-record-last-moments-of-star-devoured-black-hole.aspx
Search and Rescue beacons developed at Goddard have helped locate more than 46,000 people through Cospas-Sarsat, an international cooperative system for search and rescue.
Now Maryland-based Concentric Real Time LLC has licensed a 2nd generation of this technology to be used by individuals who carry personal locator beacons in case of emergency. The 2nd generation technology allows for higher-resolution signaling that produces highly accurate location results. Learn more about NASA technology available for licensing at:
https://lnkd.in/eUDZCWY
Learn more about the new licensed technology at: https://lnkd.in/eJ9WQMK
Aerospace Corporation:
Massive THANK YOU to the firefighting crews who saved the historic Mt. Wilson Observatory when it was threatened by the #BobcatFire. Our
MAFIOT Project is among the major space observation programs being housed at the site.
Read: https://lnkd.in/gMtXhsH
“We are grateful to the firefighters who put their lives on the line to battle the fire around the facility,” said Dave Cardoza, the Principal Director of Aerospace's Electronics and Photonics Laboratory. “The fact that the structures are still standing is a testament to the dedication that they put into their jobs. This will allow us to continue our important work on the mountain.”
Collins Aerospace wins contract to improve anti-jamming for warfighters:
The United States Army awarded Collins Aerospace a Phase III contract to build the second generation of its Mounted Assured Position Navigation and Timing System (MAPS). Learn more about the MAPS program.
https://www.gpsworld.com/collins-aerospace-wins-contract-to-improve-anti-jamming-for-warfighters/
The future of the U.S. Coast Guard is in outer space:
The #USCG and outer space? CAPT Michael Sinclair at Brookings explores the possibilities of leveraging advances in space technology to facilitate the execution of the Coast Guard’s 11 statutory missions here on
earth.
https://www.brookings.edu/blog/order-from-chaos/2020/10/15/the-future-of-the-u-s-coast-guard-is-in-outer-space/?preview_id=1071241
APN-086 Datum Transformations & Plate Tectonics Compensation:
For information on the above, please click this link here.
Timing is Everything: To Protect Geospatial and the World, We Need Bullet-proof Time:
https://www.gwprime.geospatialworld.net/opinion/timing-is-everything-to-protect-geospatial-and-the-world-we-need-bullet-proof-time/
Planes continue to fly into a GPS dark hole over the Mediterranean, puzzling experts - Fortune:
https://fortune.com/2020/11/01/planes-ships-gps-mediterranean-russia-syria-north-korea/
GSA releases 3rd GNSS User Technology Report - GPS World:
The European GNSS Agency (GSA) released its latest GNSS User Technology Report, providing a comprehensive analysis of
GNSS trends and developments. Get an overview of the report:
https://www.gpsworld.com/gsa-releases-3rd-gnss-user-technology-report/
NASA Science:
Particles smaller than an atom hurtle through the universe nearly at the speed of light, blasted into space from something, somewhere, in the cosmos. A scientific collaboration of the Pierre Auger Observatory, including researchers from the University of Delaware, has measured the most powerful of these particles — ultra-high-energy cosmic rays — with unprecedented precision. In doing so, they have found a “kink” in the energy spectrum that is shining more light on the possible origins of these subatomic space travelers. The team’s findings are based on the analysis of 215,030 cosmic ray events with energies above 2.5 quintillion electron volts (eV), recorded over the past decade by the Pierre Auger Observatory in Argentina. It is the largest observatory in the world for studying cosmic rays.
https://www.linkedin.com/pulse/new-feature-found-energy-spectrum-universes-most-alvin-lieberman-/?trackingId=IlRSPhN6ioWXqKvErDTwmw%3D%3D
AI Facts Every Dev Should Know: Artificial intelligence is older than you, probably!:
https://paper.li/The-Helen-Jackson-Daily#/
Timekeeping Theory Combines Quantum Clocks and Einstein’s Relativity:
https://www.dartmouth.edu/press-releases/timekeeping-theory-combines-quantum-clocks-and-einsteins-relativity.html
Allie K. Miller at Amazon:
Forbes AI Innovator of the Year | Artificial Intelligence at Amazon | LinkedIn Top Voice 2019 | 750K+ followers
This home can fold and unfold in 10 minutes. Anyone else love researching the future of construction, real estate, and urban development?
Source: Mashable (Please search Google for this)
WTO: EU can impose tariffs on $4 billion of U.S. goods:
https://www.upi.com/Top_News/World-News/2020/10/13/WTO-EU-can-impose-tariffs-on-4-billion-of-US-goods/1551602609900/
Featured Innovator: Kaitlin Moore:
Meet Kaitlin Moore, an atomic physicist in the field of #quantum science and #engineering at our Applied Sciences division. There, she and the team she’s part of are spearheading advancements in the potentially world-changing realm of #quantumsensing and #quantumcommunications.
Read more about our latest featured innovator: https://bit.ly/2HPxv7R
On October 5th, the Real-Time Working Group of the International GNSS Service (IGS) will release the first version of the new IGS-SSR standard! It will be accessible at:
https://lnkd.in/dY3EVry.
The IGS SSR format is an open standard for dissemination of real-time products to support the
IGS Real-Time Service and the wider community. The messages support multi-GNSS and include corrections for orbits, clocks,
DCB's, phase-biases and ionospheric delays. Extensions to also cover satellite attitude, phase center offsets and variations and group delay variations are planned in the near future. The goal is to create a self-contained and scalable standard for a wide range of real-time applications.
International GNSS Service.
On 9 December 2020, this new (incoming) website will be moved from its temporary home on igscb.org to our main website,
IGS.org. The content in the current (outgoing) IGS.org website will be archived.
Also on 9 December 2020, ALL FTP access to ftp://ftp.igs.org
will be permanently terminated and replaced with a secured https://files.igs.org/
. Data, content, and directory hierarchy will remain unchanged.
Precise time for all: Paper calls for resilient national timing - GPS World:
https://www.gpsworld.com/precise-time-for-all-paper-calls-for-resilient-national-timing/
https://www.linkedin.com/pulse/precise-time-all-paper-calls-resilient-national-timing-dana-a-goward/?trackingId=zBSdfU3cvbOkIz2B5vehjg%3D%3D
GNSS simulator companies help pilots find their way:
Find out how GNSS is playing a role in enhancing safety and training when using flight simulators
https://www.gpsworld.com/gnss-simulator-companies-help-pilots-find-their-way/
How many Global Navigation Satellite System do you know? Only GPS? GPS and
GLONASS?:
Check the right answer in the book "An Introduction to GNSS..." from NovAtel Inc.
https://lnkd.in/ePEhgwp
P.S.: Don't forget to pay attention to two regional systems!
GPS/GNSS industry recollections and predictions from the GPS World Editorial Advisory Board - GPS World:
Members of the GPS World Editorial Advisory Board share their memories and thoughts about the GPS industry over the past 30 years. Find out what they had to say.
https://www.gpsworld.com/gps-gnss-industry-recollections-and-predictions-from-the-gps-world-editorial-advisory-board/
Timing is Everything: To Protect Geospatial and the World, We Need Bullet-proof
Time:
https://www.gwprime.geospatialworld.net/opinion/timing-is-everything-to-protect-geospatial-and-the-world-we-need-bullet-proof-time/
The shape of water: bathymetry in action - GPS World:
Population growth in coastal areas and sea level rise due to climate change are driving the need for bathymetric data for planning and emergency management. Learn more about bathymetry and how the data is used.
https://www.gpsworld.com/the-shape-of-water-bathymetry-in-action/
MGUE Increment 2 contracts awarded to Rockwell Collins, L3 and Raytheon - GPS World:
The U.S. Space Force’s Space and Missile Systems Center awarded the Military Global Positioning System User Equipment (MGUE) Increment 2 Miniature Serial Interface with Next-Generation ASIC to Rockwell Collins, L3 Technologies and Raytheon Technologies. Get more details.
https://www.gpsworld.com/mgue-increment-2-contracts-awarded-to-rockwell-collins-l3-and-raytheon/
Space Force planning a ‘disruptive’ acquisitions command - SpaceNews:
Gen. John Raymond said the Space Systems Command will include a mix of legacy and nontraditional procurement offices.
https://spacenews.com/space-force-planning-a-disruptive-acquisitions-command/
US Navy plans to raise new fleet in Indo Pacific, says top US official:
I’ve been advocating for this since 2001: First Fleet. It’s back, and it’s
Area of Operation (AO) will be SE Asia and the Indian
Ocean. Wizard.
#usn #usnavy #1stFleet #scs #India #Singapore #Australia #IO #indopacific
https://www.straitstimes.com/world/united-states/us-navy-plans-to-raise-new-fleet-in-indo-pacific-says-top-us-official
Boeing subsidiary ready to launch satellite de-orbiting experiment:
https://spaceflightnow.com/2020/11/19/boeing-subsidiary-ready-to-launch-satellite-deorbiting-experiment/
SpaceX's Falcon 9 rocket with the U.S.-European Sentinel-6 Michael Freilich satellite rolled out for launch this afternoon! This #SeeingTheSeas mission is set for liftoff tomorrow at 12:17 p.m. EST (5:17 p.m.
UTC):
Join the virtual NASA Social and watch with us: https://lnkd.in/gqDb3CM
Russia Says U.S. Missile Defense Test Proves It Lied About Global Missile Shield:
https://www.newsweek.com/russia-us-missile-test-lied-global-shield-1548803
(May 2021) U.S. Army’s Terrestrial Layer Prototype Readies for Delivery:
Getting capability to soldiers on the battlefield faster is our mission. We’re working with the U.S. #Army to rapidly develop the Terrestrial Layer System,
which will help soldiers better address signals found in the immediate electromagnetic environment.
Resilient PNT critical to maritime advancement:
The International Maritime Organization has issued a resolution for maritime cyber-risk management effective in January 2021.
https://www.gpsworld.com/resilient-pnt-critical-to-maritime-advancement/
(May 2021) Space debris endangers GPS - GPS World:
By Ken Eppens, Founder and CEO, OrbitGuardians.com
19% of tracked space objects threaten GPS and other GNSS satellites. While there are much fewer objects in
MEO than in LEO, the risk in the former is
arguably greater because GPS is so critical to almost all of our technology.
The Risk:
GNSS satellites, especially GPS satellites, are critical to the well-being and smooth functioning of economies and national security. This is especially
true in Europe and the United States, which do not have complementary terrestrial systems able to provide vital positioning, navigation and timing
(PNT)
services when signals from space are not available.
While the probability of debris damage to GNSS in medium Earth orbit (MEO) is much less than for satellites in low Earth orbit
(LEO), the consequences
of such an event would be much, much higher. The loss of one satellite would be a concern; that of multiple satellites, a major problem. The unthinkable chaos,
national security damage, and severe economic impacts to the $21 trillion U.S. GDP make the risk unacceptable.
For those who think we need not worry about the low probability of collisions at
MEO, the Galileo collision avoidance maneuver in March 2021 should
be a wakeup call. The problem is here. We need to act now.
READ MORE: https://www.gpsworld.com/space-debris-endangers-gps/
(May 2021) New Automotive GNSS/INS Positioning Family for ADAS and Autonomy:
Hexagon|NovAtel has new PIM222A automotive GNSS for advanced driver assistance systems & autonomy. Precise positioning, velocity, attitude. #autonomy
#ADAS #driverlesscars #autonomouscars https://bit.ly/3hNFzGf
https://insidegnss.com/new-automotive-gnss-ins-positioning-family-for-adas-and-autonomy/
(May 2021) Telecom groups press president, Congress for GPS alternatives - GPS World:
May 25, 2021 - By Dana Goward
America urgently needs alternatives to GPS and the government must fund efforts to make that happen. So say separate documents sent to President Biden and
senior members of Congress earlier this month.
On May 6, the government’s National Security Telecommunications
Advisory Committee (NSTAC) issued its “Report to the President on Communications Resiliency.”
The next day the industry group Alliance for Telecommunications Industry
Solutions (ATIS) sent letters to Congress. Both organizations identify the need for
alternatives to GPS to support telecommunications and other critical infrastructure. Both also urge government funding for the effort.
NSTAC is a federal advisory committee composed of 18 members from the telecommunications industry.
Most are CEOs and very senior leaders in companies
such as AT&T, Microsoft, and Iridium.
This month’s NSTAC report highlights the critical role that PNT, especially timing, plays in telecommunications. It notes that
widespread use of GPS makes
the system vulnerable to a host of threats. To address this, the group recommends the administration consider an approach “similar to that reflected in the
Resilient Navigation and Timing Foundation’s paper entitled “A Resilient National Timing Architecture.” Further, to enhance the ability of commercial
entities to afford leveraging this architecture, the Administration should appropriate sufficient funds to lay the foundation for creating this timing
architecture, with the Federal Government being the first customer for what will ultimately become a resilient, interconnected network for PNT delivery.”
Federal funding is necessary, according to the board, because free GPS services eliminate market demand for alternatives.
ATIS sent letters to leaders in the House and Senate citing an “urgent need” for funding deployment and adoption of
GPS alternatives for use in critical
infrastructures, including telecommunications.
ATIS develops standards and other technical deliverables for information and
communications technology (ICT) and services companies on a broad range of
issues, including 5G and the Internet of Things (IoT).
Network and system synchronization is key for telecommunications. At present
this is done almost exclusively using signals from GPS. ATIS had previously
documented in reports and letters to Congress the vulnerability of GPS signals and the need for complementary and alternative systems to use when GPS is
not available.
The letters outline the criticality of precision timing to critical infrastructure, industries, first responders, and U.S. government entities. They cite
applications such as E9-1-1 and Assisted GPS used to find wireless
handsets, as well as critical infrastructure networks, as some of the applications at
risk.
ATIS also endorsed the findings of a recent Department of Transportation
(DOT) report to Congress. That report documented that there exist “suitable,
mature and commercially available technologies” able to provide alternatives to GPS.
Also mentioned was the appropriateness of government funding. “The role of government in protecting its citizens suggests an imperative to safeguard the
capabilities of critical infrastructure industries by facilitating resilient PNT.”
Some in previous administrations had questioned whether it was necessary and appropriate for the government to fund GPS alternatives. According to
NSTAC and
ATIS, the answer is “yes” to both.
While the Biden administration has not made any official statements on the matter, reports of conversations with recent appointees seem to indicate that
they agree with the need for government funding. There also seems to be bipartisan support for this view.
As one example, Ms. Diana Furchtgott-Roth, a conservative economist who served in the Trump administration as the leader for civil
PNT issues, supports
government funding wholeheartedly. At a recent webinar she indicated that the national need is beyond the business model of any company.
“Just as the
government funds national defense, it should also provide a complement to
GPS,” she said.
The NSTAC “Report to the President on Communications Resiliency” can be found.
ATIS letters to members in the House can be found here:
https://www.atis.org/wp-content/uploads/2021/05/House-Re-Urgent-Need-for-Alternative-Positioning-Navigation-and-Timing-Systems-Funding.pdf
and to members in the Senate here:
https://www.atis.org/wp-content/uploads/2021/05/Senate-Re-Urgent-Need-for-Alternative-Positioning-Navigation-and-Timing-Systems-Funding.pdf
(May 2021) “Investment in a 21st-century Intelligent & Autonomous Infrastructure is among the highest priorities for stimulating economic
expansion,
national security, and job growth. Edge computing, 5G
wireless, Intelligent Transportation Systems, RESILIENT APNT, and
resilient electrical grids
will drive the largest infrastructure buildout in our nation's history.”
Autonomy Institute
https://youtu.be/9-w0G7sD8NQ
Which recent GNSS/INS innovations have been most helpful in advancing bathymetry? Which upcoming ones will be?:
https://www.gpsworld.com/editorial-advisory-board-pnt-qa-advancing-bathymetry/
(May 2021) China's space ambitions target satellites, a US vulnerability - Nikkei Asia:
Blog Editor's Notes: This article hits so many of the strategic concerns around US over-reliance on GPS. And it is from a source in Japan, a country
probably even more worried about China than the U.S., if that is possible.
The article sub-head says everything: "American military's reliance on Earth orbit creates Achilles' heel."
Yet a recent GAO report says DOD is not looking seriously at GPS alternatives and is still planning to have
GPS as the centerpiece of its navigation
strategy going forward.
And further on in the article: "Losing satellite function would leave the American military like a giant whose central nervous system has been damaged."
It also points out that, with satellites out of the picture, a conflict, such as a dispute in the straits of Taiwan, could come down to more conventional
forces. Let's see... who has more troops, sailors, and equipment, and who can get them there the quickest...?
Follow the READ MORE link at the bottom of the post to see the whole article.
China's space ambitions target satellites, a US vulnerability:
American military's reliance on Earth orbit creates Achilles' heel
HIROYUKI AKITA, Nikkei commentator
May 26, 2021 19:45 JST
TOKYO -- When China landed a probe on Mars this month, President Xi Jinping hailed the success of the mission as well as the status of Beijing's burgeoning
space program.
"The landing left a Chinese mark on Mars for the first time," he said, per Xinhua News Agency. "It is another landmark progress in China's space industry
development."
The Tianwen-1 mission resulted in China becoming only the second country to land a rover on Mars successfully, after the U.S. In 2019, China accomplished
the first successful landing of a probe on the far side of the moon. Beijing last month launched a central unit of its space station, with plans to complete
the base in 2022.
Beyond the scientific or military interests, China's push into space is fueled fundamentally by Beijing's ambition to become a superpower and catch up with
the U.S.
"It requires absurdly huge costs and comes with risk to send humans into space," said Kazuto Suzuki, a University of Tokyo professor and expert on security
in space. "If the aim is purely militaristic, it would only require launching sophisticated satellites. But they build a space station, go to the moon, and
probe Mars because they want to demonstrate China's technological advancements to its people and the international community."
READ MORE: https://asia.nikkei.com/Spotlight/Comment/China-s-space-ambitions-target-satellites-a-US-vulnerability
Services Infusing AI into Air, Land, Sea Robots:
https://www.nationaldefensemagazine.org/articles/2020/10/26/services-infusing-ai-into-air-land-sea-robots
New algorithm could unleash the power of quantum computers:
A new algorithm that fast forwards simulations could bring greater use ability to current and near-term quantum computers, opening the way for applications to run past strict time limits that hamper many quantum calculations. “Quantum computers have a limited time to perform calculations before their useful quantum nature, which we call coherence, breaks down,” said Andrew Sornborger of the
Computer, Computational, and Statistical Sciences division at Los Alamos National
Laboratory, and senior author on a paper announcing the research. “With a new algorithm
that we have developed and tested, we will be able to fast forward quantum simulations to solve problems that were previously out of reach.”
https://www.lanl.gov/discover/news-release-archive/2020/October/1005-quantum-computer-algorithm.php
Schools Weren't Prepared for a Crisis Like COVID-19:
How did schools' planning *before* the pandemic affect their transitions to remote learning when COVID-19 hit? Results from our new national survey provide some insights.
https://www.rand.org/pubs/research_reports/RRA168-3.html?utm_campaign=&utm_content=1601825340&utm_medium=rand_social&utm_source=linkedin
Ada Lovelace Day is a worldwide celebration of the achievements that women have made in STEM industries, which stands for science, technology, engineering, and
math.
The day is about increasing the profile of females in STEM. The hope is that by doing this we will help to create new role models for women all across the globe and encourage more females to take roles within STEM sectors.
WOMEN IN TECH - Global Movement Nadia Mannell Carine de Meyere Candyce Costa A IDM Lindalia Sofia Junqueira Reis Isabel Velarde, Founder, CEO Innovation Hub Consulting® Dr. Cara Antoine Claudia Mendes Silva Elina Valeeva Jenyfer Maisonneuve Joanna Carson Mandi Gunsberger, GAICD Polina Vasilenko Monika Rizovska Katerina Trajchevska Melissa Slaymaker
Tactical Airborne Laser Weapon System (TALWS):
https://www.youtube.com/watch?v=rLav0zMHut8&feature=share
Hexagon launches autonomy kits for agriculture with demo tractor - GPS World:
Hexagon’s Autonomy and Positioning division has launched its first autonomy positioning and sensing kits for the agriculture market. Learn more about the kits, which the company validated in its new autonomous research and development tractor.
The evolution of GPS satellites and their use today - GPS World:
From Cold War origins of a chirping beach ball traveling through space 63 years ago, now more than 2,600 satellites enhance our terrestrial lives. Here's how satellite technology has gotten to this point. (Photo: U.S. Army/DARPA) #satellite #technology
https://www.gpsworld.com/the-evolution-of-gps-satellites-and-their-use-today/
Norway Govt Wants GPS Backup - Offering $910K To Develop for Maritime Pilots
https://www.linkedin.com/pulse/norway-govt-wants-gps-backup-offering-910k-develop-maritime-goward/?trackingId=XwGTaSqa8QQSen61VOFpeg%3D%3D
Blog Editor's (Dana A. Goward) Notes:
Less than a million dollars (US) doesn't seem like much to develop a navigation system.
Also, there are existing systems already developed (or nearly there) that could be implemented. But they certainly cannot be had for such a small sum.
Perhaps the Norwegian government just wants to fund a study.
But why is a study needed? The problem of GNSS disruption in maritime has already been addressed by the European
Space Agency (ESA), of which Norway is a member in good standing.
Last year ESA's NAVISP program sponsored a very comprehensive, year-long study of requirements and solutions for resilient maritime navigation. The 1,100 pages of reports of the MarRINav project outline process, findings, results and recommendations in great detail. True, it was written with a focus on the
UK, but the methodology and results can be applied anywhere.
We hope that this announcement isn't just a way for government leaders to give the appearance of action so it doesn't have to actually do anything.
No alt text provided for this image
(Technical Weekly)
Most of the pilots have experienced GPS failure. Now they want to develop a safer alternative
Over the next few months, the Norwegian Coastal Administration will announce NOK 8.5 million to those who can develop a secure backup for satellite navigation.
The senses, local knowledge and radar are the most important tools the pilots use for unloading ships safely in port, but they have increasingly become dependent on satellite navigation such as
GPS. These signals can be lost, either by accident or as a result of deliberate hacking.
- It can lead to dangerous situations and unwanted incidents, says Odd Sveinung Hareide, advisor and project manager in the pilot service.
The pilotage service will therefore in November announce a contract of NOK 8.55 million for someone who can develop a backup solution for satellite navigation. The new sensor technology will be able to compensate for the unreliability of satellite navigation and warn when the signals are affected.
Basically, it should be a mobile solution that can be used by the pilotage service, but the goal is that the solution can also be used in shipping in general.
The goal is to sign the development contract in early 2021. The finished prototype is scheduled to be ready in 2023.
READ MORE Site has a header button for version in English (but TeK Associates
could not find it!)
Very Long Baseline Array (VLBA) Makes First Direct Distance Measurement to
Magnetar:
Fenton Heirtzler, Organic materials chemistry and nonlinear optics:
"Very cool! Thanks for the enlightenment on magnetars (I had never heard of them). Maybe you could amend your posting to include the distance which was measured?
Would it be reasonable to assume that there are no other heavenly bodies anywhere nearby to this?
Can this thing be considered a massive ferromagnetic object, and is there any way to learn what its atomic composition would be?
There are other speculative questions, but I assume that at this point in time, there are no answers for them...."
RL Poole, Author, The Leedskalnin Codex: Breakthroughs in Understanding the Coral Castle - #1 Best Seller in the Physics of Gravity (Amazon Kindle):
"I read the Wikipedia reference. It says in the same place, that these magnetic fields are a hundred million times stronger than any man-made
magnet."
Fenton Heirtzler:
" Is there any pop science magazine article on this...? I am afraid I wouldn't know. I think that is a question better directed at Google. I watched a science program about magnetars years ago, and found them fascinating.
"Classical magnetism occurs when the nuclear spins of atoms are spatially aligned (I think). So is a magneton one big unidirectional nuclear spin ?" Says, who?
Magnetars are FASCINATING."
Free navigation tutorials (from China and Andover, MA): (THK: Danger)
Precise Navigation Made Simple:
ACEINNA’s inertial solutions deliver high precision in an easy-to-use open source development environment. Our fully temperature calibrated solutions deliver the performance needed to sense the real-world motion of today’s intelligent systems.
(THK: Danger)
https://www.aceinna.com/inertial-systems?gclid=EAIaIQobChMI7sH95dr26wIVgp-zCh3vqAdkEAMYASAAEgLoZvD_BwE
Vulnerabilities of GPS is a big concern: Dana Goward - Geospatial World:
Satellite systems have become an integral part of our businesses for precise navigation and timing services. Yet GPS/GNSS jamming, spoofing, and other forms of interference appear to be growing in frequency and severity. Recently, the Senate Armed Services Committee (SASC) asked Pentagon to provide Combatant Commander’s alternate position, navigation and timing (PNT) systems to GPS within two years.
We caught up with Dana Goward, a member of the National PNT Advisory Board, and President & Director of RNT Foundation, an independent, member-supported non-profit that works in the area building awareness about the importance and vulnerabilities of navigation and timing systems, encourages development and implementation of resilient terrestrial systems, and advocates for policies to deter spoofing and jamming. Goward is retired from the federal Senior Executive Service having served as the maritime navigation authority for the United States. He has represented the US at IMO, IALA, the UN anti-piracy working group, and other international forums. He is also a Senior Adviser to Space Command’s Purposeful Interference Response Team.
Why is there so much concern around vulnerabilities of GPS?
It’s not just about GPS; all GNSS signals are weak. They are 20,000 km above the Earth, powered by solar panels, and are transmitting all the time, after all. Just as a matter of physics, it’s very easy to block a relatively weak signal. That is what GPS jamming is. Also, because the different global navigation satellites systems want to increase their user base, they release all the information about their signals so they can be integrated into other systems. But if you know exactly what the signals look like, you know how to imitate them. This makes the signals open to spoofing as well. That is another significant challenge, because, in many ways spoofing is worse than jamming — instead of no information, spoofing can give you hazardously misleading information.
ALSO READ: Why Resilient PNT Infrastructure is Imperative to Global Economic Growth
All GNSS are relatively the same signal strength and in same general frequency band, and they are all in space. Naturally, they are subjected to same kind of vulnerabilities — severe solar activity, malicious high-power electro-magnetic pulses, local jamming, spoofing, etc. Even urban canyons and downtown cities are a challenge as the signals tend to bounce off buildings and can cause problems for receivers. Using multiple GNSS systems at the same time does protect users a bit if one of the systems suffers a cyberattack or an equipment failure. So, it does offer some measure of additional resilience. But, generally, they all have similar vulnerabilities and are subject to the same threats, so the added resilience and security is marginal.
These shared vulnerabilities have been a concern for some time. There are all kinds of incentives for individuals and organizations to interfere with GPS signals — from delivery drivers taking long breaks, to criminal organizations wanting to divert a shipment, to nations looking to counter the armed forces of another. For example, American generals have said that Syria and the Middle East have the highest intensity of electronic warfare anywhere on the face of the planet. A lot of that is GPS/GNSS jamming and spoofing.
Interestingly, a recent sampling by the European Union found 500,000 instances of transmissions on GNSS frequency that should not have been there. About 10% of them were determined to be malicious and intentional, while the others were just apparently accidental. So, there are a lot of vulnerabilities in the system, and a lot of real-world threats
From cellular networks to power grids to transport systems, GNSS is the source of accurate, synchronized time for almost everything. A 2012 Boston Consulting Group study found that the geospatial services fueled by GPS resulted in $1.4 trillion a year in savings to the US economy and another $1.6 trillion in added revenues. A London Economics study found that if
GPS/GNSS went away for five days, the UK economy would suffer losses of £5.2 billion, which translates to $482 billion per year.
We are fortunate that nothing really bad has happened so far. At the RNT Foundation we encourage responsible governments to try to get ahead of things and prevent mishaps, rather than waiting for them to happen before swinging into action.
Tell us about the details of the FCC-Ligado controversy?
Ligado is really an interesting case. Ligado Networks, an American satellite communications company, claims they want to establish a low-power nationwide
5G network. And it has been allotted space in the L-band spectrum which is the same band as that of
GPS and other GNSS. US government tests have shown that these transmissions will interfere with
GPS reception for many users. Naturally, a lot of organizations and individuals, including the Executive branch of the government, are concerned about its possible impact on
GPS and are of the opinion that we shouldn’t go ahead with this. However, the
Federal Communications Commission, which is an independent agency and works on its own under a congressional mandate, is convinced that this isn’t going to be that much of a problem, approved the request, and is refusing to budge.
Ever since, the opposition to the proposal has been growing. The entire executive branch of the government, including the Department of Defense and Department of Transportation, have amplified their protest and a number of organizations including the RNT Foundation, have formerly requested that the
FCC reconsider their decision. Now, there is some legislation in Congress to examine the decision. The end of that story is yet to be written.
One of my thoughts here is that the FCC is the ‘communications’ commission, not the ‘navigation’ or ‘geospatial’ commission. Radio communications are different from radio navigation in a lot of ways. In fact, they are almost opposites — in radio communications you are blasting the 1s and 0s through the surrounding noise to get the message through, while in radio navigation you look down within the background noise for the 1s and 0s. And rather than identifying the 1s and 0s as the message in communications, radio navigation precisely measures the time of the change from a 1 to a 0 so the receiver can figure out its location. There are a bunch of other differences as well.
It could well be that the radio and communications engineers at FCC didn’t have the right context to evaluate the Ligado proposal as it would affect navigation. As an example — I was on a panel with the head of Ligado who is a communications engineer. I said there were tests that found Ligado transmissions violated the government safety buffer for
GPS failures. I said that, rather than using the safety buffer in its tests, Ligado had tested the
GPS receivers to the point of failure. Ligado’s CEO replied that they hadn’t done that. They had just tested the receivers to where they started “giving bad information.” OK, so that’s worse. Bad information is worse than no information at all.
But it shows the difference between the way communications engineers and navigation engineers view things. In communications, a little bit of interference might not be so bad. You could probably understand the overall message. Or, if it is two-way communications, you could ask for a repeat. Not so for navigation. One of the first signs of interference with
GPS/GNSS signals in many receivers is bad, potentially hazardous, information. A safety report to
NASA last year detailed how a passenger aircraft nearly crashed into a mountain because of this kind of interference with its
GPS receiver.
https://www.gwprime.geospatialworld.net/building-resilient-future-for-pnt/
FAA gives go-ahead for Amazon drone-delivery tests - GPS World:
Amazon received Federal Aviation Administration approval to use drones to deliver packages. Find out what this could mean for package delivery times.
https://www.gpsworld.com/faa-gives-go-ahead-for-amazon-drone-delivery-tests/
Collaboration aimed at GNSS solution for IoT modems - GPS World
Synopsys Inc and Nestwave are collaborating to combine Nestwave’s geolocation software with the
Synopsys DesignWare ARC IoT Communications Subsystem for a complete low-power GNSS solution for integration into IoT modems. Get more details. (Image: metamorworks/iStock/Getty Images Plus/Getty Images)
#GNSS #IoT #communications
https://www.gpsworld.com/collaboration-aimed-at-gnss-solution-for-iot-modems/
Impact of UK Jamming Trials - More Details
https://www.linkedin.com/pulse/impact-uk-jamming-trials-more-details-dana-a-goward/?msgControlName=reply_to_sender&msgConversationId=6711409108978810880&msgOverlay=true&trackingId=k628VEwizHd988URzFPD2Q%3D%3D
And here is the notice:
2nd September 2020 SW2020/187
Jamming trial impacting electronic situational awareness devices, UAS command systems and GNSS receivers: 8 Sep – 4 Dec, Luce Bay
Jamming activity will take place 8 September – 4 December 2020 in and around Luce
Bay. The activity may affect GNSS receivers along with UAS and cockpit devices operating on 433, 868, 915, 2400, 5800 MHz operating up to 40,000FT
AMSL within 55NM of 545020N 045548W (West Freugh).
During the trials impacted systems may suffer intermittent or total failure. Individual events will not exceed 2 minutes in duration with no more than 5 events per hour. Activity will take place in daytime hours between
0830 and 1600.
For further information contact spectrum@caa.co.uk
Emergency cease jamming contact 01776 888932 or 01776 888930
First Fix: New year, new opportunities for GNSS industry - GPS World:
As we embark on a new year, 2021 ushers in a new administration and the start of the 117th Congress. With these changes comes a litany of opportunities, as well as challenges, for the nearly four-decade-old GPS industry, says the GPS Innovation Alliance (GPSIA)'s J. David Grossman.
https://www.gpsworld.com/first-fix-new-year-new-opportunities-for-gnss-industry/
Aviation Policy News: Airline Bailouts and Revenue Sources for Air Traffic Control During Pandemic:
https://reason.org/aviation-policy-news/airline-bailouts-and-revenue-sources-for-air-traffic-control-during-pandemic/
SAE International EDGE Report: Air Traffic Management:
https://www.linkedin.com/pulse/sae-international-edge-report-air-traffic-management-james-farrell/?trackingId=R9GWb7Yb4z4weE1PFCuVCg%3D%3D
Building a better aerial imagery program beyond UAVs:
https://www.gpsworld.com/building-a-better-aerial-imagery-program-beyond-uavs/
New Photon-Counting Camera Captures 3D Images with Record Speed and Resolution:
https://www.linkedin.com/pulse/new-photon-counting-camera-captures-3d-images-record-lieberman-/?trackingId=mgULTu7tmhZMONZj%2FmBEiA%3D%3D
Researchers have developed the first mega-pixel photon-counting camera based on new-generation image sensor technology that uses single-photon avalanche diodes (SPADs). The new camera can detect single photons of light at unprecedented speeds, a capability that could advance applications that require fast acquisition of 3D images such as augmented reality and LiDAR systems for autonomous vehicles.
https://www.osa.org/en-us/about_osa/newsroom/news_releases/2020/new_photon-counting_camera_captures_3d_images_with/
Distributing high-precision time over optical networks in the 5G world - GPS World:
Mobile operators are investing heavily in the deployment of LTE-Advanced and 5G networks that will transform cellular communications and connectivity. Check out some challenges they face.
https://www.gpsworld.com/distributing-high-precision-time-over-optical-networks-in-the-5g-world/
No silver bullet for US PNT: Many sources needed - GPS World:
At the moment, the U.S. GPS provides the vast majority of PNT services in the U.S. and around the world. Yet, like all space-based systems, its signals are weak and very vulnerable to interference. (Image: DOT) #GPS
#PNT #space
https://www.gpsworld.com/no-silver-bullet-for-us-pnt-many-sources-needed/
Enemy jammer takes first test flight aboard EA-18G Growler:
https://www.upi.com/Defense-News/2020/08/24/Enemy-jammer-takes-first-test-flight-aboard-EA-18G-Growler/1031598294824/
Securing PNT Workshop Looks at GNSS Back-up Options - Inside GNSS:
http://insidegnss.com/securing-pnt-workshop-looks-at-gnss-back-up-options/
http://gpsworld.com/australia-invests-in-gps-sbas-technology-for-national-positioning/
https://www.talen-x.com/threatblocker?mc_cid=1e62019cb8&mc_eid=450b4cc973&utm_campaign=1e62019cb8-EMAIL_CAMPAIGN_2018_07_16_07_02&utm_medium=email&utm_source=All%2B(2018)&utm_term=0_3fae09a5ac-1e62019cb8-107521725
https://insidegnss.com/ligado-related-lawsuit-recommences-january-2/
https://www.harris.com//content/gps3
Multipath GNSS signals are a threat to timing receivers in 4G and 5G networks - Spirent
Blog:
https://itsf2020.executiveindustryevents.com/Event/Programme/programme.php
https://www.spirent.com/blogs/the-impact-of-5g-on-location-technologies-part-1-market-drivers
https://rntfnd.org/wp-content/uploads/Resilient-National-Timing-Architecture-16-Oct-2020.pdf
Friday 04/17/2020 Ligado / FCC Roundup - What might really happen:
https://www.linkedin.com/pulse/friday-ligado-fcc-roundup-what-might-really-happen-dana-a-goward/
https://www.state.gov/support-for-5g-and-internet-of-things-development/
https://ecfsapi.fcc.gov/file/1041636716512/Ligado%20dismissal%20letter%20(4.16.20).pdf
https://insidegnss.com/lead-up-to-impending-ligado-decision-started-with-10-years-of-testing-and-controversy/
https://www.lightreading.com/5g/ligado-receives-poisoned-chalice/d/d-id/758960#.XpjGnW8oLuA.linkedin
FCC Chairman Moves Forward on Ligado Approval - Inside GNSS:
https://www.linkedin.com/pulse/fcc-chairman-moves-forward-ligado-approval-inside-gnss-goward/?trackingId=MFgQXL1Eqa%2BgyuB22a8cQg%3D%3D
Attorney General William P. Barr’s Statement on FCC Chairman Pai’s Draft Order to Approve Ligado’s Application to Facilitate 5G and Internet of Things Services:
https://www.justice.gov/opa/pr/attorney-general-william-p-barr-s-statement-fcc-chairman-pai-s-draft-order-approve-ligado-s
FCC Chairman Moves Forward on Ligado Approval Interfering with GPS:
The Federal Communications Commission announced April 16 that Chairman Ajit Pai is circulating a draft proposal within the Commission that would approve a plan by Ligado Networks to use frequencies neighboring those used by GPS
for a 5G terrestrial service.
https://insidegnss.com/fcc-chairman-moves-forward-on-ligado-approval/
"On November 18th 2020, the Federal Communications Commission unanimously voted to value streaming video and entertainment above human life." - Debby Bezzina, MBA,PMP, Managing Director for CCAT.
Debby was featured on the Michigan Department of Transportation's Talking Michigan Transportation Podcast.
For more of her insights on the recent FCC ruling, listen here: http://myumi.ch/bvPVY
#SaveTheSafetySpectrum #DSRC #CV2X
NATO’s new tool shows the impact of GPS jammers:
https://www.c4isrnet.com/newsletters/military-space-report/2020/04/15/natos-new-tool-shows-the-impact-of-gps-jammers/
NATO’s new tool shows the impact of GPS jammers - C4ISRNet (More):
https://www.linkedin.com/pulse/natos-new-tool-shows-impact-gps-jammers-c4isrnet-dana-a-goward/
https://www.c4isrnet.com/newsletters/military-space-report/2020/04/15/natos-new-tool-shows-the-impact-of-gps-jammers/?utm_source=Sailthru&utm_medium=email&utm_campaign=Space%2004.15.20&utm_term=Editorial%20-%20Military%20Space%20Report
https://www.c4isrnet.com/electronic-warfare/
Now Operational, BeiDou Could Conceal Cybersecurity Threat:
https://insidegnss.com/now-operational-beidou-could-conceal-cybersecurity-threat/
Defense Secretary Fires on FCC about Ligado - What else to remember:
https://www.linkedin.com/pulse/defense-secretary-fires-fcc-ligado-what-else-remember-goward/?trackingId=8TDFKawotAxKNslcgZ63LA%3D%3D
It is clear that Defense Secretary Esper is upset with the FCC for dismissing his concerns about national security and
Ligado out of hand. The below article documents some of his frustration. This article is a pretty good opening salvo for tomorrow's hearing by the Senate Armed Services Committee.
As we go into tomorrow's hearing, though, there are a couple things to keep in mind that we have not heard about at all in the media to date,
First, the FCC giving away (no charge to Ligado other than application fees) this satellite spectrum for terrestrial use means it won't be available for space assets. We understand the L-Band is ideal for space-based PNT. So if we want any more of it (like the LEO systems Chinese are building and the US Air Force is experimenting with) our options are going to be that much more limited. Spectrum is a finite resource.
Second, we didn't need to be here. The executive branch has long said that we need to take better care of our GPS and PNT with: 1) a system to detect and identify disruption sources; 2) far wider use of receivers that reject many forms of interference; and 3) signals from a terrestrial system that would stabilize GPS signals in receivers making them very resistant to interference, and provide PNT when GPS isn't available at all.
The Pentagon made its case against Ligado. What now? - C4ISRNet:
https://www.linkedin.com/pulse/pentagon-made-its-case-against-ligado-what-now-c4isrnet-goward/
https://www.c4isrnet.com/battlefield-tech/2020/05/06/the-pentagon-had-made-its-case-against-ligado-what-comes-next-isnt-clear/
https://www.c4isrnet.com/battlefield-tech/2020/04/17/key-defense-committee-members-consider-legislation-to-block-fccs-ligado-move/
Pai to Congress "You're Wrong" - FCC fires back on Ligado Decision:
Blog Editor's (Dana A. Goward) Note: The more we read materials from each side of this issue, the more the opponents seem to be talking past each other. They might as well be speaking different languages. Everyone sees themselves as doing the right thing and is puzzled by why the other side sees them as in error at best and a force for evil at the worst.
We are sure that everyone is trying to do the right thing, but there are clearly some fundamental disconnects as to how folks see the world, interpret data, from testing, etc.
That is why we have called for an independent expert evaluation of the testing results and a cost-benefit analysis so as to better inform public policy decisions.
Chairman Pai Letter to House Armed Services Committee Chair Adam Smith
In a letter to Congressman Adam Smith, Chair of the House Armed Services
Committee, last week, FCC Chairman Ajit Pai refuted claims that he and the unanimous, bipartisan vote of the Commission had erred in their decision on Ligado Networks.
https://rntfnd.org/wp-content/uploads/Chairman-Pai-Response-to-Smith-05-26-20.pdf
Over the course of four pages he said that:
- National security and the safety of the public was a critical concern for him and the commission
- He would never do anything to compromise safety and security
- There is a fundamental misconception that the FCC has authorized "sharing" spectrum. GPS has not (sic) right to operate in the spectrum allocated to
Ligado.
- Regarding consultation with the Department of Defense
"... the Department of Defense was provided with numerous opportunities over nearly a decade to provide the
Commission with any relevant evidence it wished to submit."
The commission considers all comments provided for the docket and formally sought comments six separate times over the course of nine years.
The commission provided DoD, via NTIA, a draft order to consider in October 2019.
He (Chairman Pai) personally spoke to the Secretary of Defense and other senior
DoD officials on the matter
- The FCC's process and decisions are not impugned just because another agency doesn't like the outcome
- FCC's excellent career staff worked for years on technical analysis supporting the decision.
- FCC did not violate the law regarding the need to "resolve concerns." Paragraphs 129 and 130 of the order did that.
- DoD never offered a classified briefing (if they had, he would have taken it), nor did they enter into the record any testing results.
All five FCC Commissioners responded to Chairman Smith's letter. Here are copies of all the letters:
https://www.linkedin.com/pulse/pai-congress-youre-wrong-fcc-fires-back-ligado-decision-goward/?trackingId=9Fy7rS5ITSCYkInQwy9QDw%3D%3D
FCC’s Ligado decision broadens, deepens opposition - GPS World
https://www.linkedin.com/pulse/fccs-ligado-decision-broadens-deepens-opposition-gps-dana-a-goward/?trackingId=Dj45Ji4wz4ZIPT5S5IdsvA%3D%3D
Last week, 27 members of the U.S. House Agriculture Committee sent a letter to Federal
Communications Commission Chairman (FCC) Ajit Pai. In it, they urged him to reconsider the FCC’s decision to allow Ligado Networks to operate a terrestrial nationwide network that the executive branch says will cause harmful interference to
GPS signals for many users. This concern and opposition from a sector not traditionally engaged in
GPS or positioning, navigation and timing (PNT) issues is just one example of how the FCC’s decision — rather than putting the issue to rest — has instead recruited a whole new set of actors from across multiple sectors for the opposition.
Many observers don’t see this as surprising.
According to one observer, previously it was easy for many to assume the FCC would reject Ligado’s proposal. The entire executive branch had been vehemently opposed for years. So had aviation groups, the weather community, geospatial interests and some satellite communications concerns. With such opposition from so many important quarters, it was reasonable for many to assume they need not become involved. Now that the
FCC has acted to the contrary, these interests have become well energized.
The FCC decision also empowered opponents to educate and recruit others who don’t normally think or worry about
GPS and PNT issues, folks like farmers and agricultural interests.
As one insider said, “The existing opposition can now go to just about anyone in any sector and say, ‘This is going to happen and it will harm your operation. There are no ifs, ands, or buts. The FCC has decided’.”
Agriculture’s reliance on GPS
Agriculture is a good example. While not the sector that first springs to mind when most people think about GPS, farming has become dependent on augmented
GPS for precisely and automatically driving machinery, minimizing fertilizer and pesticide use, and a wide variety of other productivity gains over
pre-GPS operations. “GPS is critically important to the commercial agriculture, mining, forestry and rural manufacturing industries. In fact,
GPS has become the single most significant technological advancement for American farm equipment in the past two decades… [A 2019 RTI study] found that during planting season, if
GPS were interrupted, the economic impact to the agriculture sector could amount to losses of $15 billion due to lower crop yields. Moreover, an earlier study suggested GPS-enabled precision agriculture could save farmers an estimated 10 to 15 percent in operating costs and purchased inputs. This same study estimated the benefits of GPS to precision agriculture between $10 and $17 billion.”
Department of Transportation studies have shown that high-precision GPS receivers, such as those used in agriculture, could be impacted within 3,000 meters of a Ligado transmitters. With tens of thousands of transmitters deployed in a nationwide network, this could pose a real problem for American farming.
Other sectors have also become involved in the opposition. The recently formed Keep GPS Working Coalition has members representing aviation, surface transportation, maritime, agriculture and equipment manufacturing.
This formal and public coalition, though, seems to be just the tip of the opposition iceberg.
Almost 100 dissenting organizations:
According to some involved with protesting the FCC’s decision, there are nearly a hundred organizations and companies that are working in some way to have it overturned. These include multiple aviation, delivery service, agriculture, surface transportation, geospatial, weather, maritime, space and technology interests.
One sign of the influence they are having is an increase in concerns being expressed by members of Congress.
There’s a growing need for positioning solutions for Advanced Driver-Assistance Systems (#ADAS) in #autonomous vehicles. #GNSS-reliant vehicles require lane-level resolution in order to navigate safely and reliably. Additional sensors are used to enhance this accuracy, but what role does GNSS play in these sensor suites?
Hexagon | NovAtel technical sales rep Kevin Doherty explains how GNSS is integrated into R&D through series production to deliver #autonomy and #positioning - assured.
Watch now >> https://hxgn.biz/2C4LGmq
FCC Chooses a bit more 5G over aviation safety. Again!:
https://www.rtca.org/news/aviation-groups-call-for-halt-of-fcc-spectrum-auction-affecting-radar-altimete/#:~:text=The%20group%20requested%20that%20the,altimeters%20prior%20to%20the%20auction.
The #UAE has taken an exciting leap in the #spaceeconomy with its recent successful launch
of the Hope spacecraft to #Mars.
By sometime in Feb of next year (2021) it will enter a Martian orbit and begin collecting, analyzing and transmitting Mars atmospheric, climate and weather data.
The launch used #Japan H-IIA rockets from Japan’s Tanegashima Space Center and with contract support from Mitsubishi Heavy Industries. The
UAE used a unique approach to build the spacecraft themselves deploying strong academic
coordination.
Given the UAE success already from the project by both staying on its $200M
budget and short timetables it is likely to serve as a new model for other nations #Space �� ambitions.
https://www.theverge.com/2020/7/19/21330417/uae-hope-spacecraft-emirates-mars-mission-launch-success
U.S. Department of Transportation announces drone Remote ID partners - GPS World:
https://www.gpsworld.com/u-s-department-of-transportation-announces-drone-remote-id-partners/
A new, more secure GPS signal could be ready by 2020:
https://www.c4isrnet.com/battlefield-tech/2019/08/21/a-new-more-secure-gps-signal-could-be-ready-by-2020/
How Vulnerable Is G.P.S.?
An engineering professor has proved—and exploited—its vulnerabilities. by Greg Milner August 6, 2020
The proliferation of G.P.S. interference is a major reckoning for the country’s military and defense systems.
In the cool, dark hours after midnight on June 20, 2012, Todd Humphreys made the final preparations for his attack on the Global Positioning System. He stood alone in the middle of White Sands Missile Range, in southern New Mexico, sixty miles north of Juárez. All around him were the glowing gypsum dunes of the Chihuahuan Desert. In the distance, the snow-capped San Andres Mountains loomed.
On a hill about a kilometre away, his team was gathered around a flat metal box the size of a carry-on suitcase. The electronic machinery inside the box was called a spoofer—a weapon by another name. Soon, a Hornet Mini, a drone-operated helicopter popular with law-enforcement and rescue agencies, was scheduled to appear forty feet above them. Then the spoofer would be put to the test.
https://www.newyorker.com/tech/annals-of-technology/how-vulnerable-is-gps
https://www.newyorker.com/tech/annals-of-technology
http://www.navcen.uscg.gov/pdf/loran/geninfo/GPS_Backup_For_PNT_Aug_2006.pdf
Technology establishes your Position, Navigation, and Time (PNT) in the environment -- but we have to protect it.
Defend your #PNT in challenging environments through Hexagon | NovAtel anti-jam antennas, interference mitigation, and GNSS+INS combined systems.
Read more about how to protect the integrity of your PNT solution >> https://hxgn.biz/2RM4zg9
https://novatel.com/industries/defense/
Feds outline all the ways they can get you for messing with drones:
The Advisory on the Application of Federal Laws to the Acquisition and Use of Technology to Detect and Mitigate Unmanned Aircraft Systems was jointly issued by the Justice Department, Federal Communications Commission, Department of Homeland Security, and Transportation Department. It starts out noting that Congress has only given the authority to those four departments plus the Department of Energy to do such things. No other entities, including state, local, and tribal law enforcement, are allowed - and presumably could be sanctioned if they did so.
When talking about measures that involve jamming or spoofing GPS, the advisory cites 18 U.S.C. § 1367, Interference with the Operation of a Satellite that "...generally prohibits “obstruct[ing] or hinder[ing] any satellite transmission.”
We will try to avoid any snarky comments about the FCC's decision on Ligado Networks at this point...
https://docs.fcc.gov/public/attachments/DOC-366222A1.pdf
The National Geodetic Survey (NGS) recently announced two new items related to the modernized National Spatial Reference System. Check out the updates.
https://www.microchip.com/design-centers/synchronization-and-timing-systems?utm_source=gpsworld.com&utm_medium=DisplayAd&utm_content=FTS_970x90&utm_campaign=BlueSkyv2.0wDHSLaunch
https://www.gpsworld.com/ngs-releases-modernized-national-spatial-reference-system-updates/
ESA project calls for terrestrial navigation systems to reduce risk
https://www.gpsworld.com/esa-project-calls-for-terrestrial-navigation-systems-to-reduce-risk/
Webinar to discuss MarRINav project results:
In 2018 the first-ever European Radionavigation Plan said “It is recognized that
GNSS should not be the sole source of PNT information. Alternative PNT systems, not necessarily using radio frequencies, should thus be put in place where the criticality of the application requires it.”Graphic from MarRINav report showing system of systems approach to
PNT resilience and reliability. In 2019 the European Space
Agency (ESA) published a permanent open call for proposals for positioning, navigation, and timing studies and systems, including those that had nothing to do with space.
One of the first fruits of this is the ESA-funded Maritime Resilience and
Integrity of Navigation project, or MarRINav, recently completed by researchers in the United Kingdom.
“Maritime navigation and port operations are critical for almost every nation,” said Jonathan Turner, one of the
MarRINav project team. “As an island nation with a strong maritime heritage, we in the United Kingdom perhaps have an even greater appreciation of this.” Turner is co-founder of the blue economy solutions company
NLA International, which led a team of eight organizations cooperating on the project.
While MarRINav focused its analysis on the United Kingdom, the intent was to provide information, and an analysis framework, that could also be used by other nations.
Maritime is one of sectors most dependent upon Global Navigation Satellite Systems, according to the project reports, and one of the ones with the greatest awareness of
GNSS vulnerabilities and their consequences. MarRINav concludes that integrity and resilience are two of the most important parameters for maritime navigation.
Maritime is also one of the sectors most ready to integrate space and terrestrial navigation systems, according to the report’s authors. The International Maritime Organization has already introduced a performance standard for a
Multi-System Receiver, or MSR, that will incorporate a wide variety of navigation signals.
Despite the distractions of Brexit over the last four years, the United Kingdom has been particularly focused on its vulnerability to
GNSS outages.
Eyeing Russia, Army fields jam-resistant GPS in Europe:
https://www.c4isrnet.com/show-reporter/c4isrnet-conference/2019/06/06/eyeing-russia-army-fields-jam-resistant-gps-in-europe/
U.S. Space Command blasts Russia for anti-satellite missile test -
SpaceNews (Why, because they did not use an F-15 double thruster instead?):
https://spacenews.com/u-s-space-command-blasts-russia-for-anti-satellite-missile-test/
US Air Force selects Raytheon Missiles & Defense to develop Long-Range Standoff weapon:
https://www.prnewswire.com/news-releases/us-air-force-selects-raytheon-missiles--defense-to-develop-long-range-standoff-weapon-301043337.html
What we know about Iran’s counter-space weapons:
https://www.c4isrnet.com/battlefield-tech/space/2020/01/08/what-we-know-about-irans-counter-space-weapons/
Norway says Russia jammed GPS signal during NATO drill:
https://www.c4isrnet.com/electronic-warfare/2018/11/13/norway-says-russia-jammed-gps-signal-during-nato-drill/
https://www.linkedin.com/pulse/gps-disruptions-spread-south-from-russia-saudi-arabia-dana-a-goward/
https://www.linkedin.com/pulse/gps-tracker-shows-child-90-miles-from-school-dana-a-goward/
https://navcen.uscg.gov/?Do=GPSReportStatus
https://www.linkedin.com/pulse/us-military-denial-over-space-joint-force-quarterly-dana-a-goward/
https://www.linkedin.com/pulse/security-satnav-experts-agree-gps-cybersecurity-issue-dana-a-goward/
http://insidegnss.com/security-and-satnav-experts-agree-gps-is-a-cybersecurity-issue/
https://www.linkedin.com/pulse/first-responders-combating-single-point-failure-domestic-goward/
https://www.domesticpreparedness.com/resilience/combating-the-single-point-of-failure/
Norway Powerless Against GPS Interference - NRK:
https://www.linkedin.com/pulse/norway-powerless-against-gps-interference-nrk-dana-a-goward/
https://rntfnd.org/2017/12/15/norway-especially-in-the-line-of-fire-for-gps-jamming/
Russia’s new navigation plan reveals a fear of jamming - C4ISRNet:
https://www.linkedin.com/pulse/russias-new-navigation-plan-reveals-fear-jamming-c4isrnet-goward/?trackingId=H6DeC6N7a6UdpSUpRATl8w%3D%3D
https://rntfnd.org/wp-content/uploads/CIS-Russia-Radionav-Plan-2019-2024.pdf
In addition to jamming NATO exercises and spoofing GPS receivers to protect VIPs, Moscow also claims it added GPS jammers to over 250,000 domestic cell towers to help defeat U.S. cruise missiles should they attack.
Letter to Karen Van Dyke (DOT): http://rntfnd.org/wp-content/uploads/Alliance_for_Telecommunications_Industry_Solutions_ATIS_Copper_Optical_Access_Synchronization_and_Transport_Committee_COAST-2.pdf
https://www.linkedin.com/pulse/8-airports-30-days-4243-gps-denial-events-strike3-dana-a-goward/
https://www.linkedin.com/pulse/earths-magnetic-north-shifting-rapidly-whats-mean-gnss-dana-a-goward/
https://www.upi.com/Science_News/2019/01/14/Magnetic-Norths-erratic-behavior-forces-update-to-global-navigation-system/1611547434485/
Communication and Navigation Satellite Signal Broadcast Histories and Interruptions:
Please click menu items scattered around the top for a more detailed view.
I just ran across this overview summary: http://mgex.igs.org/analysis/index.php
https://www.gpsworld.com/survey-accuracy-the-future-of-precision-with-5-gnss-constellations/
My
Speculation on the cause of Boeing 737 MAX 8 Failure
FCC to approve spectrum plan that Pentagon claims will harm GPS - C4ISRNet
https://www.linkedin.com/pulse/fcc-approve-spectrum-plan-pentagon-claims-harm-gps-c4isrnet-goward/?trackingId=lcUjp8OCm31t0jGU09V04A%3D%3D
https://www.c4isrnet.com/breaking-news/2020/04/10/fcc-to-approve-spectrum-plan-that-pentagon-claims-will-harm-gps/
Congressmen demand answers after Pentagon issues GPS warning - C4ISRNet:
https://www.linkedin.com/pulse/congressmen-demand-answers-after-pentagon-issues-gps-warning-goward/?trackingId=gDKUytGx8bBHp2Dm6rbkkw%3D%3D
https://rntfnd.org/wp-content/uploads/2020-04-10-DeFazio-Garamendi-Letter-to-DOT-GPS.pdf
(Chao's letter)
In response to this filed by Ligado:
https://rntfnd.org/wp-content/uploads/Ligado-Ex-Parte-Re-NTIA-Submission-4.12.2020.pdf
Resolution scheduled here:
https://ecfsapi.fcc.gov/file/10410288301607/NTIA%20Letter%20to%20FCC%20Chairman%20Re%20Ligado%20Applications%204.10.20.pdf
Multi-agency Report Opposing Ligado Request Could Be Last Element in Controversy - Inside
GNSS:
https://www.linkedin.com/pulse/multi-agency-report-opposing-ligado-request-could-last-dana-a-goward/?trackingId=Ta1leL2lgR1Xl4B%2FAEVgMg%3D%3D
https://insidegnss.com/memo-from-13-top-agencies-opposing-ligado-request-could-end-this-round-of-controversy/
Senate Armed Services, Former FCC Commissioner Slam Ligado:
https://www.linkedin.com/pulse/senate-armed-services-former-fcc-commissioner-slam-ligado-goward/?trackingId=d1UQE62LjbadaEq43gJwwg%3D%3D
It’s Time for the FCC to Terminate the ‘LightSquared’ Proceeding:
https://morningconsult.com/opinions/its-time-for-the-fcc-to-terminate-the-lightsquared-proceeding/
17 December 2020-Coalition supports NDAA provisions to protect GPS against Ligado - GPS World:
The Keep GPS Working Coalition issued a statement in support of the inclusion of provisions related to
GPS in the National Defense Authorization Act.
Check it out now: https://www.gpsworld.com/coalition-supports-ndaa-provisions-to-protect-gps-against-ligado/
New Executive Order regarding PNT:
https://www.linkedin.com/pulse/positioning-navigation-timing-executive-order-welcomed-dana-a-goward/?trackingId=ewh0SwJVLGGUoxDDX7InXg%3D%3D
https://www.nextgov.com/ideas/2020/03/positioning-navigation-and-timing-executive-order-welcomed-mixed-reactions/163630/
Industry perspective: Next-gen PNT needs careful assessment:
https://www.gpsworld.com/industry-perspective-next-gen-pnt-needs-careful-assessment/
Three obstacles are slowing space sensors for hypersonic threats:
https://www.linkedin.com/pulse/three-obstacles-slowing-space-sensors-hypersonic-alvin-lieberman-/?trackingId=qo3kTgtYXFePtum%2FWz6arA%3D%3D
https://www.c4isrnet.com/space/2020/04/08/three-obstacles-are-slowing-space-sensors-for-hypersonic-threats/
Four Challenges to Hypersonics:
https://www.lockheedmartin.com/en-us/capabilities/space/executive-blog-rick-ambrose-scott-greene-lmiq.html?_lrsc=d754421c-446b-4b11-ae40-4b147ab99ea3
Pentagon's Top R&D Chief Throws Cold Water On Laser Missile Defense Aspirations:
"Turn out the lights - the Party is over" Marketing flacks can go find something else to do for a few years instead of hawking concepts from movies based on comic books. Directed Energy lost its key advocate.
https://lnkd.in/g8yhnTm
https://www.thedrive.com/the-war-zone/33584/pentagons-top-rd-chief-throws-cold-water-on-laser-missile-defense-aspirations
Six months of reported GPS issues:
https://navcen.uscg.gov/?Do=GPSReportStatus
Analysis and Overview:
https://www.linkedin.com/pulse/six-months-gps-problem-reports-dana-a-goward/?trackingId=29G7wQPAe2FLuyX%2BM4UVwg%3D%3D
https://insidegnss.com/progress-logged-on-strengthening-and-backing-up-pnt/
Lockheed’s Skunk Works Team to Help Update Air Force Reconnaissance Aircraft Avionics:
https://www.govconwire.com/2020/04/lockheeds-skunk-works-team-to-help-update-air-force-reconnaissance-aircraft-avionics/
DHS S&T Invites Critical Infrastructure Owners and Operators to GPS Spoofing Test Event - HS Today:
https://www.linkedin.com/pulse/dhs-st-invites-critical-infrastructure-owners-operators-goward/?trackingId=Ckj5qMIVHXVOv1PBnYPZvg%3D%3D
New GPS 'circle spoofing' moves ship locations thousands of miles - GPS World:
New research by Bjorn Bergman of the environmental non-profit SkyTruth has found ships in various parts of the world reporting locations thousands of miles away and circling at precisely 20 knots.
https://www.gpsworld.com/new-gps-circle-spoofing-moves-ship-locations-thousands-of-miles/
COSMIC-1 mission for GPS reflectometry comes to an end - GPS World
The COSMIC-1 program ended last month, when the last of six tiny satellites were decommissioned. Find out how long the satellites were in space.
https://www.gpsworld.com/cosmic-mission-for-gps-reflectometry-comes-to-an-end/
The Department of Homeland Security (DHS), Science and Technology Directorate (S&T) announced today an opportunity for critical infrastructure owners & operators and Global Positioning System (GPS) equipment manufacturers to test their equipment against GPS spoofing. The 2020 GPS Testing for Critical Infrastructure (GET-CI) event will be held later this year and is the third in this series of test opportunities.
https://www.hstoday.us/subject-matter-areas/infrastructure-security/dhs-st-invites-critical-infrastructure-owners-and-operators-to-gps-spoofing-test-event/
Modernizing SIGINT—Technology Adapts to Serve Multiple Missions and Masters:
In this month’s Journal of Electromagnetic Dominance, I have a discussion with John Haystead about the evolving relationship between Signals Intelligence and electronic support measures, and the blurring of the lines between SIGINT, communications intelligence, and electronic intelligence. Spectrum dominance is the key for our
DoD customers, and BAE Systems is poised at the forefront of innovation in this discriminator. At the end of the day, situational awareness across a variety of missions in as compact, efficient and upgradeable a package as possible is the goal. To read more on this important technology, check out May’s feature article in
JED.
https://www.jed-digital.com/jedm/0520_may_2020/MobilePagedArticle.action?articleId=1585383&utm_source=hootsuite&utm_medium=facebook&utm_term=bae%20systems%20electronic%20systems&utm_content=9e2ef039-c8f9-416e-83d8-c56037362f6e&utm_campaign=ES2020#articleId1585383
More Jamming and Spoofing of GPS:
https://www.gpsworld.com/report-dod-drone-spoofed-gps-on-small-aircraft/
https://spacenews.com/northrop-grumman-to-develop-jam-resistant-payload-for-u-s-military-communications-satellites/
Click here to see some other aspects of GPS
evolution.
Brad Parkinson’s 2017 wish
list: https://rntfnd.org/wp-content/uploads/Three-Wishes-v11s.pdf
Click here to see MORE aspects of GPS
evolution. https://www.septentrio.com/en/applications/referencestations
USDOT seeks university to help secure automated navigation:
https://www.gpsworld.com/usdot-seeks-university-to-help-secure-automated-navigation/
Raytheon, to replace OCX hardware by 2022 for $378 million:
https://spacenews.com/raytheon-to-replace-ocx-hardware-by-2022-for-378-million/
The War perpetrated by Others on GPS (Part II) and other updates:
https://www.linkedin.com/pulse/great-questions-q-from-how-america-losing-gps-war-part-dana-a-goward-1e/
https://www.ursanav.com/wp-content/uploads/Resilient-Timing-and-UTC-Service.pdf
https://www.gpsworld.com/cobham-secures-uk-contract-for-gnss-anti-jamming/?
https://www.gpsworld.com/raytheon-to-replace-computer-hardware-on-new-gps-ground-system/
https://www.gpsworld.com/final-steps-underway-to-operationalize-new-gps-m-code-signal/
GPS III - Misleading Sound Bites Harm Nation - National Defense:
https://www.linkedin.com/pulse/gps-iii-misleading-sound-bites-harm-nation-national-dana-a-goward/?trackingId=wZHZweHcDxx3l8%2Bm%2BEfRPQ%3D%3D
https://www.nationaldefensemagazine.org/articles/2020/4/13/gps-iii---misleading-sound-bites-harm-nation
PCCW Global and UniStrong to link GNSS tech with telecoms, airports - GPS World:
PCCW GLOBAL Limited and UniStrong APAC Pte Ltd will collaborate on developing GNSS technologies and services for the telecommunications and aviation industries. Read more on the partnership and their goals.
https://www.gpsworld.com/pccw-global-and-unistrong-to-link-gnss-tech-with-telecoms-airports/
Second GPS III Satellite Declared Ready for Military Use:
https://www.satellitetoday.com/government-military/2020/03/25/second-gps-iii-satellite-declared-ready-for-military-use/
GPS Backup Analysis Stays on Track:
https://insidegnss.com/gps-backup-analysis-stays-on-track/
https://www.linkedin.com/pulse/gps-backup-analysis-stays-track-inside-gnss-dana-a-goward/?trackingId=%2FSPse84lJ7frU38cZqC1hQ%3D%3D
If your GPS position, navigation and time are under threat from jamming, then you need to consider NovAtel® Anti-Jam antennas. These are designed to defend against sources of interference -- that's assured positioning.
Read more about NovAtel®'s GPS Anti-Jam Technology >> https://hxgn.biz/2zl1vEp
A new system, called WarLoc, makes it possible to locate warfighters and first responders in GPS-denied environments.
Read more about the system, created by Robotic Research, LLC. (Photo: Robotic Research)
#GPS:
https://www.gpsworld.com/warloc-locates-foot-soldiers-in-gps-denied-areas/
CHC Navigation introduces Apache3 marine drone - GPS World:
The 2020 Apache3 Marine Drone provides a series of new features and additional enhancements to make lake, river and coastal hydrographic surveys more productive, according to maker CHC Navigation. Learn more about the drone. (Photo: CHC Navigation) #drone
#marine #survey:
https://www.gpsworld.com/chc-navigation-introduces-apache3-marine-drone/
TeK Associates follows novel INS developments and relative INS accuracies: Familiar with Electro-statically supported
Gyro (ESG) such as the airborne Micro, the SSBN ESG, as well as that in the
Gravity-Probe satellite), Laser Gyros, Fiber
Optics Gyros, Wine glass\tuning fork gyros, Microelectromechanical
systems (MEMS) Gyroscopes. Prof. Christopher Jekeli’s
(Ohio University, Columbus, OH) published
mathematical model for Cold-Atom
Gyros, as well as conventional
mechanical spinning rotor gyros and their analysis.
We follow evolving procedures for moving platform shipborne
and in-air alignment gyro-compassing and alternative
mechanizations: Local Level, Space-Stable, Wander-Azimuth, Strapdown and associated
transformations (and typical frequency of re-calculation sample
rates). Surprisingly, new insights have recently been offered that much of
the technology harkens back to analog gyro behavior more than is currently
necessary in this digital age of extremely high processing speeds which can now
support relatively high external GPS updates within strapdown gyroscope
implementations. Previous notions of coning, sculling, the dynamics of Schuler
loop oscillations being activated, or 24 hour diurnal oscillations are no longer
necessary in Navigation systems mechanized with MEMS throughout and with
GPS or
differential GPS updates on the order of seconds or minutes because the gyros no
longer need to go open loop without a compensating and ameliorating
external “navaid”
fix for anything that approaches a significant fraction of
the ~hour and a half Schuler period [30].
We are familiar with typical operational constraints and weapon
system accuracies of
several military platforms as well: e.g., Ships Submersible
Ballistic Nuclear (SSBN’s) submarines (a.k.a.
“Boomers”),
Ships Submersible Nuclear (SSN) submarines (a.k.a.,
“attack”
subs), which allied country’s
submarines use
“degaussing”
coils and which use
“flash”,
“deperm”
procedures, etc.
We are also familiar with the tenets, details, and history of
“Search and Screening”: e.g., detection
range, worse case detection threats, observables-in-the-military-sense,
countermeasures and counter-countermeasures for various sensors, etc. See [1] to
[7]
for perspectives on our early experience in this area. We are also knowledgeable
in the associated terminology such as that of U.S. submarine alertness levels: 1SQ, 2SQ,...,
Operation Sanguine [before the name change in the 1970’s to evade the
scrutiny of protesters ], TACAMO, long trailing wire antenna (BCA), pig tail antenna, whip antenna,
Blue-green laser, Counter
Value vs. Counter Force, Mid-course star fix, firing keys (where
located and who has access, and orderly sequence of events, and expected
synchronizations and chain-of-command), etc.

Our SSBN submarines can launch while submerged;
while those of many other countries must surface first before they can launch.
We are cognizant of the Society of Old
Crows, of the
Countermeasures Handbook (we possess several back issues), and Paladin Press
publications over the years (that should never have been allowed to appear). CV
motion models, Lamps helicopters and ships, use of ship-borne winch and
cables dropped from helicopters seeking to land onboard in rough seas (where
cable is secured to winch and helicopter pulls cable taught and is reeled in
slowly so that Helicopter motion automatically matches that of the deck of the
ship as both pitch, roll, and yaw together (to avoid damaging the helicopter
with a nasty unexpected impact with the deck of the much more massive ship
capable of preserving inertia by inflicting a severe impulse force as a big
crushing blow over the short period of time-BANG!) We know about historical
“pipe dreams”
that failed miserably as well as alternative more robust approaches (using older
technology) that was good enough without being vulnerable to a myriad of
difficulties associated with other things going wrong (one example being trying
to use a laser-based reflection system to guide the helicopter to land on the
deck in rough seas-obvious vulnerabilities being: fog, battle smoke, electronic
failures at an extremely critical time a’la
Murphy’s law, laser
orientation capability for interacting with surface ship’s
deck-in-motion possibly falling out of sufficient calibration [as needed to
retrieve the necessary reflection close to perpendicular to the moving deck for
instantaneous round trip timing-so you can’t
solve the problem until you have already solved the problem] and needing
additional INS components with their additional costs and vulnerabilities and
operational procedures). Thank Michael Athans and AlphaTech for the less
practical approach, described above. Example 2: What about the attempt to align
several (two or more) surface ships at sea in tandem to create an effective
landing strip for those super-sized carrier air craft to take-off and land for
re-supply at sea. Although some of their numerous computer studies demonstrated
feasibility, please just think about being in the North Atlantic with typical
winter weather conditions involving very high sea states and then try to pull
off this stunt. We have Raman Mehra and Scientific Systems to thank for this
second one. Both examples were funded by the U.S. Navy and further reported in an
open unclassified forum but my critical ear hears all and I don’t
soon forget these apparent technical boondoggles but do continue to wonder how
they ever got pass other watchdogs. I guess it pays to be well connected. It’s
not my cup of tea though. I have to
“say what I see and what I smell”.
We Kerr’s (curs) are well-known watchdogs too. We try to avoid stepping in
“it”
as our predecessors did! Sometimes we mark our territory as a good alpha dog.
Arrrooooo! Better to lead than to follow since the scenery is much better and
more interesting (as
every sled dog knows).

We are cognizant of the necessary interaction between the architectures
associated with various alternative approaches to multi-target tracking and
Kalman filter-based target tracking algorithms in use (alternative tracking
algorithms hypothesized as possible modern replacements).
Our primary strength is having an in depth awareness of all the
Kalman filter estimation-based approaches used to date for handling
failure\fault detection in an INS or in GPS RAIM, or in a GPS/INS
hybrid. We are analytic algorithm specialists. This is our area of greatest
familiarity.
Even more usefull information is
availed here following the 305 references provided immediately below (click this
link to automatically move pass these citations).
Historical Account of our experience therein:
- [1] Kerr, T. H., “Poseidon
Improvement Studies: Real-Time Failure Detection in the SINS\ESGM (U),”
TASC Report TR-418-20, Reading, MA, June 1974 (Confidential) for Navy,
SP-2413 (Jerome “Jerry” Katz).
-
- [2] Kerr, T. H., “Failure
Detection in the SINS\ESGM System (U),” TASC Report TR-528-3-1,
Reading, MA, July 1975 (Confidential) for Navy, SP-2413 (Jerome “Jerry” Katz).
-
- [3] Kerr, T. H.,
“Improving ESGM Failure Detection in the SINS\ESGM System (U),”
TASC Report TR-678-3-1, Reading, MA, October 1976 (Confidential) for
Navy, SP-2413 (Jerome “Jerry” Katz).
-
- [4] Kerr, T. H.,
“Preliminary Quantitative Evaluation of Accuracy\Observables
Trade-off in Selecting Loran\NAVSAT Fix Strategies (U),” TASC
Technical Information Memorandum TIM-889-3-1, Reading, MA, December
1977 (Confidential) for Navy, SP-2413 (Jerome “Jerry” Katz).
-
- [5] Kerr, T. H.,
“Improving C-3 SSBN Navaid Utilization (U),” TASC Technical
Information Memorandum TIM-1390-3-1, Reading, MA, August 1979 (Secret)
for Navy, SP-2413 (Jerome “Jerry” Katz)
[6] Kerr, T. H., “Modeling and
Evaluating an Empirical INS Difference Monitoring Procedure Used to Sequence
SSBN Navaid Fixes,” Proceedings of the Annual Meeting of the Institute of
Navigation, U.S. Naval Academy, Annapolis, Md., 9-11 June 1981. (Selected for
reprinting in Navigation: Journal of the
Institute of Navigation, Vol. 28, No. 4, pp. 263-285, Winter 1981-82).
[7] Kerr, T. H., “Impact
of Navigation Accuracy in Optimized Straight-Line
Surveillance\Detection of Undersea Buried Pipe Valves,” Proceedings
of National Marine Meeting of the Institute of Navigation (ION),
Cambridge, MA, 27-29 October 1982.
[8]
Kerr, T. H., “Stability Conditions for the RelNav Community as a
Decentralized Estimator-Final Report,” Intermetrics, Inc. Report No.
IR-480, Cambridge, MA, 10 August 1980, for NADC (Warminster, PA).
[9]
Kerr,
T. H., and Chin, L., “A Stable Decentralized Filtering Implementation
for JTIDS RelNav,” Proceedings of
IEEE Position, Location, and Navigation Symposium (PLANS), Atlantic
City, NJ, 8-11 December 1980.
(
Kerr,
T. H., and Chin, L., “A Stable Decentralized Filtering Implementation
for JTIDS RelNav,” Proceedings of
IEEE Position, Location, and Navigation Symposium (PLANS), Atlantic
City, NJ, 8-11 December 1980.
)
[10] Kerr, T. H., and Chin, L.,
“The Theory and Techniques of Discrete-Time Decentralized Filters,”
in Advances in the Techniques and
Technology in the Application of Nonlinear Filters and Kalman Filters,
edited by C. T. Leondes, NATO Advisory Group for Aerospace Research and
Development, AGARDograph No. 256, Noordhoff International Publishing,
Lieden, 1981.
[11] Kerr, T. H., and Rogers, R.,
“Report on PINS Filter Design Review (of Magnavox),”
Intermetrics Memo, Cambridge, MA, 11 August 1983, for NOSC (San Diego, CA).
(Minesweeper Navigation)
[12]
Kerr, T. H., “GPS\SSN Antenna Detectability,” Intermetrics Report No.
IR-MA-199, Cambridge, MA, 15 March 1983, for NADC (George Lowenstein).
[13] Kerr, T. H., “Functional and
Mathematical Structural Analysis of the Passive Tracking Algorithm (PTA),”
Intermetrics Report No. IR-MA-208, Cambridge, MA, 25 May 1983, for NADC. (LAMPS
Sonobuoy algorithms.)
[14] Kerr, T. H., “Navy GPS\SSN
Phase II User Equipment DT&E Magnavox Modification Center (Mod Center) Test
Report,” 1 June 1985, for NADC Code 4022 (George
Lowenstein).
[15] Kerr, T. H., “Navy GPS\SSN
Phase II User Equipment DT&E Rockwell-Collins Modification Center (Mod
Center) Test Report,” 1 June 1985, for NADC Code 4022 (George
Lowenstein).
[16] Kerr, T. H., “Navy GPS\SSN
Phase II User Equipment DT&E Rockwell-Collins Developmental Test and
Evaluation (Operational Readiness) [DT&E (OR)] Test Report,” 10 June 1985,
for NADC Code 4022 (George Lowenstein).
[17] Kerr, T. H., “Magnavox
Military Utility Test Report,” 10 June 1985, for NADC Code 4022 (for
George
Lowenstein).
[18] Kerr, T. H., “Phase III GPS
Integration; Volume 1: GPS U.E. Characteristics,” Intermetrics Report
IR-MA-177, Cambridge, MA, January 1983, for Navair and for NOSC (Richard Akita).
[19] Kerr, T. H., “Decentralized Filtering and Redundancy Management Failure Detection for Multi-Sensor Integrated Navigation
Systems,” Proceedings of the National Technical Meeting of the Institute of Navigation (ION), San Diego, CA, 15-17 January 1985.
[20] Kerr, T. H., “Use of GPS\INS
in the Design of Airborne Multisensor Data Collection Missions (for Tuning
NN-based
ATR algorithms),” the Institute of Navigation Proceedings
of GPS-94, Salt Lake City, UT, pp. 1173-1188, 20-23 Sept. 1994.
[21] Kerr, T. H., “Further Comments
on ‘Optimal Sensor Selection Strategy for Discrete-Time Estimators’,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 31, No. 3, pp. 1159-1166,
June 1995.
[22]
Kerr,
T. H., “Sensor Scheduling in Kalman Filters: Evaluating a Procedure for
Varying Submarine Navaids,” Proceedings
of 57th Annual Meeting of the Institute of Navigation, pp.
310-324, Albuquerque, NM, 9-13 June 2001.
[23]
Kerr, T. H.,
“Sensor
Scheduling in Kalman Filters: varying navaid fixes for trading-off submarine NAV
accuracy vs. ASW exposure,” Proceedings
of The Workshop on Estimation, Tracking, and Fusion: A Tribute to Yaakov
Bar-Shalom (on the occasion of his 60th Birthday) following the Fourth
ONR/GTRI Workshop on Target Tracking and Sensor Fusion, Naval
Postgraduate School, Monterey, CA, pp. 104-122, 17 May 2001.
[24]
Kerr, T. H.,
“Further Critical Perspectives on Certain Aspects of GPS Development
and Use,”
Proceedings of 57th Annual Meeting of the Institute of
Navigation, 9-13 June 2001.
(To see a high level overview slide show associated with the topics of the
preceding paper, please click here to obtain the main
executable file “stpete.exe”.
In order to view
the slideshow, user must first also download these auxiliary files: this associated
.DLL file, then this .DLL file, then this
VBX file, all to the same folder location on their local computer, where “stpete.exe”
resides. Our Website host required temporary conversion
to exclusively lower case spellings. Once this is done, merely click on “stpete”.exe
to start the show and click on screen to move to the next screen in the sequence
until the end [when it closes and stops].)
[25] Biezad, D. J., Integrated Navigation and Guidance Systems,
AIAA Education Series, Reston, VA, 1999.
[26] Sofir, I., “Improved
Method for Calculating Exact Geodetic Latitude and Attitude-Revisited,”
AIAA Journal of Guidance, Control, and Dynamics, Vol. 23, No. 2, ff. 369,
2000.
[27] Siouris, G. M., “Navigation:
Inertial,” Encyclopedia of Physical Science and Technology, 2nd
Edition, V. 10, pp. 595-647, Academic Press, NY, 1992.
[28] Jordan, J. F., Wood, L.
J., “Navigation:
Space Missions,” Encyclopedia of Physical Science and Technology, 2nd
Edition, Vol. 10, pp. 649-673, Academic Press, NY, 1992.
[29] Ward, P., “Navigation:
Satellites,” Encyclopedia of Physical Science and Technology, 2nd
Edition, Vol. 10, pp. 675-702, Academic Press, NY, 1992.
[30] Farrell, J. L., “Strapdown at the
Crossroads,”
Navigation, Journal of the Institute of Navigation, Vol. 51, No. 4,
pp. 249-257, Winter 2004. (A good modern perspective!
Correction in Vol. 52, No.
1, page iii, Spring 2005. Strong conclusions in this paper should be viewed
as being somewhat controversial.)
[31] Kerr, T. H., “Comment on `Precision Free-Inertial Navigation with Gravity Compensation by an Onboard
Gradiometer’,”
AIAA Journal of Guidance, Control, and Dynamics, Vol. 30, No. 4, July-Aug. 2007.
[32] Felter, S. C., Wu, N. E., “A Relative Navigation System for
Formation Flight,” IEEE Trans. on
Aerospace and Electronic Systems, Vol. 33, No. 7, pp. 958-967, July 1997.
[33] Juang, J.-C., Huang, G.-S., “Development of GPS-Based
Altitude Determination Algorithms,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 33, No. 7, pp. 968-976,
July 1997.
[34] Chatterji, G. B., Menon, P. K., Sridhar, B., “GPS/Machine
Vision Navigation System for Aircraft,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 33, No. 7, pp. 1012-1095,
July 1997.
[35] Xiong, P., “Spacial and Temporal Processing for Global Navigation
Satellite Systems: GPS receiver paradigm,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 39, No. 7, pp. 936-948,
July 2003.
[36] Madhani, P. H., “Application of Successive Interference
Cancellation to GPS Pseudolite Near-Far Problem,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 39, No. 4, pp. 481-488,
April 2003.
[37] Luo, N., “Multiple Moving Platform, GPS, Relative Positioning,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 39, No. 7, pp. 936-948,
July 2003.
[38] Fante, R. L., “Multipath-induced bias, GPS time-of-arrival,
Evaluation and Reduction,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 39, No. 7, pp. 911-920,
July 2003.
[39] Qi, H., “GPS/INS Integration: Direct Kalman Filtering Approach,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 38, No. 1, pp. 687-693,
Jan. 2002.
[40] Shin, D.-H., “TOA and TDOA Positioning Error,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 38, No. 1, pp. 307-308,
Jan. 2002.
[41] Pervan, B., “Sigma Inflation for Local Area Augmentation of GPS,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 37, No. 10, pp. 1301-1311,
Out. 2001.
[42] Praasch, M. S., “SS-Ranging Multipath Model Validation for DGPS,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 37, No. 1, pp. 298-304,
Jan. 2001.
[43] Ray, J. K., “Carrier Multipath Mitigation, Multiantenna System,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 37, No. 1, pp. 183-195,
Jan. 2001.
[44] Kim,
K. H., Lee, J. G., Park, C. G., “Adaptive Two Stage Extended Kalman Filter for
a Fault-Tolerant INS-GPS Loosely Coupled System,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
45, No.
1, pp. 125-137, Jan. 2009.
[45] Jardak,
N., Samama, N., “Indoor
Positioning Based on GPS-Repeators: Performance Enhancement using an Open Code
Loop Architecture,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
45, No.
1, pp. 347-359, Jan. 2009.
[46] “Noncoherrent
Integrations for GNSS Detection: Analysis and Comparisons,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
45, No.
1, pp. 360-375, Jan. 2009.
[47] Chiang, K.-W., Noureldin, A.,
El-Sheimy, N., “Constructive Neural-Networks-Based MEMS/GPS Integration Scheme,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 2, pp. 582-594, April 2008.
[48] Farrell,
W. J., “Interacting Multiple Model Filter for Tactical Ballistic Missile
Tracking,” IEEE Trans. on Aerospace and Electronic Systems, Vol. 44, No. 2, pp.
418-426, April 2008.
[49] Borio, D., Camoriano, L., Lo
Presti, L., Fantino, M., “DTFT-Based
Frequency Lock Loop for GNSS Applications,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 2, pp. 595-612, April 2008.
[50] Kaplan,
L. M., “Assignment Costs for Multiple Sensor Track-to-Track Association,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 2, pp. 655-675, April 2008.
[51] Bon, N., Khenchaf, A., Garello,
R., “GLRT Subspace
Detection for Range and Doppler Distributed Targets,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 2, pp. 678-695, April 2008.
[52] Juang, J.-C., “Multi-Objective
Approach to GNSS Code Discrimination Design,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 2, pp. 481-492, April 2008.
[53] Geren, W. P., Murphy, T.,
Pankaskif, T. A., “Analysis
of Airborne GPS Multipath Effects using High-Fidelity EM Models,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 2, pp. 711-723, April 2008.
[54] Jan, S.-S., Gebre-Egziabher, D.,
Walter, T., Enge, P., “Improving
GPS-Based Landing System Performance using an Empirical Barometric Altimeter
Confidence Bound,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 1, pp. 127-146, Jan. 2008.
[55] Lambert, H. C.,
“Tracking Filter for the Mitigation of the Ionospheric Range Bias,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 1, pp. 339-348, Jan. 2008.
[56] Tudoroiu, N., Khorasani, K.,
“Satellite Fault Diagnosis using a Bank of Interacting Kalman Filters,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
43, No. 4, pp. 1334-1350, Oct. 2007.
[57] Musicki, D., La Scala, B.,
“Multi-Target Tracking in Clutter Without Measurement Assignment,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 3, pp. 877-896, July 2008.
[58] Blanch, J., Walter, T., Enge,
P.,
“Position Error Bound Calculation for GNSS Using Measurement Residuals,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 3, pp. 977-984, July 2008.
[59] Musicki, D., “Multi-Target Tracking
using Multiple Passive Bearings-Only Asynchronous Sensors,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 3, pp. 1151-1160, July 2008. Also see: http://www.gallup.unm.edu/~smarandache/NATOASI_ATJDTSPK.pdf
[60] Foster, C. C., Elkaim, G. H.,
“Extension of a Two-Step Calibration Methodology to Include Nonorthogonal
Sensor Axes,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 3, pp. 1070-1078, July 2008.
[61] Borio, D., Camoriano, L., Lo
Presti, L.,
“Impact of GPS Acquisition Strategy on Decision Probabilities,” IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 3, pp. 996-1011, July 2008.
[62] Lee, J., Pullen, S., Enge, P., “Sigma-Mean Monitoring
for the Local Area Augmentation of GPS,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 42, No. 2, pp. 625-635,
Apr. 2006.
[63] Bednarz, S., Misra, P., “Receiver Clock-Based
Integrity Monitoring for GPS Precision Approaches,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 42, No. 2,
pp. 636-643, Apr. 2006.
[64] Heo, M.-B., Pervan, B., “Carrier Phase Navigation
Architecture for Shipboard Relative GPS,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 42, No. 2,
pp. 670-679, Apr. 2006.
[65]
Pacher, M., Porter, A., Polat, M., “INS-Aiding
Using Bearings-Only Measurements of an Unknown Ground Object,”
Navigation:
Journal of the Institute of Navigation, Vol. 53, No. 1, pp. 1-20, Spring
2006.
[66]
Wendel, J., Metzger, J., Moenikes, R., Maier, A., Trommer, G. F., “A
Performance Comparison of Tightly Coupled GPS/INS Navigation Systems Based on
Extended and Sigma Point Kalman Filters,”
Navigation:
Journal of the Institute of Navigation, Vol. 53, No. 1, pp. 21-31, Spring
2006.
[67]
Farrell, J. L., “Full
Integrity Testing for GPS/INS,”
Navigation:
Journal of the Institute of Navigation, Vol. 53, No. 1, pp. 33-40, Spring
2006.
[68]
Hwang, P. Y., Brown, R. G., “RAIM-FDE
Revisited: A New Breakthrough in Availability Performance with nioRAIM (Novel
Integrity-Optimized RAIM),”
Navigation:
Journal of the Institute of Navigation, Vol. 53, No. 1, pp. 41-51, Spring
2006.
[69]
Alves, D. B. M., Monico, J. F. G., “Mitigating
Systematic Errors for Single Frequency GPS Receivers Employing A Penalized Least
Squares Methodology,” Navigation:
Journal of the Institute of Navigation, Vol. 53, No. 1, pp. 53-60, Spring
2006.
[70]
Fante, R. L., Vaccaro, J. J., “Cancellation of Jammers and
Jammer Multipath in a GPS Receiver,” IEEE
AES Systems Magazine, Vol. 13, No. 11, pp. 25-28, Nov. 1998.
[71] Fante,
R. L., Vaccaro, J. J., “Wideband Cancellation of Interference in a GPS Receive
Array,” IEEE Trans. on
Aerospace and Electronic Systems, Vol. 36, No. 2, pp. 549-564, April 2000.
[72] Counselman,
C. C., “Array Antennas for DGPS,” IEEE
Systems Magazine, Vol. 13, No. 12, pp. 15-19, Dec. 1998.
[73]
Rabideau, D. J., “Clutter and Jammer Multipath Cancellation in
Airborne Adaptive Radar,” IEEE
Trans. on Aerospace and Electronic Systems, Vol. 36, No. 2, pp. 565-583,
April 2000.
[74] Myers,
L., Improved Radio Jamming Techniques: Electronic Guerilla Warfare, ISBN
0873645200, Paladin Press, Boulder, CO, 1989.
[75] Daher,
J. K., Harris, J. M., Wheeler, M. L., “An Evaluation of the Radio Frequency
Susceptibility of Commercial GPS Receivers,”
IEEE AES Systems Magazine, Vol. 9, No. 10, pp. 21-25, October
1994.
[76] White,
N. A., “Detection of Interference/Jamming and Spoofing in DGPS-aided Inertial
Systems,” IEEE Trans. on
Aerospace and Electronic Systems, Vol. 34, No. 5, pp. 1208-1217, Oct. 1998.
[77]
White, N. A., Maybeck, P. S., DeVilbiss, S. L., “Detection of
Interference/Jamming and Spoofing in a DGPS-Aided Inertial System,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 34, No. 4
pp. 1208-1217, Oct. 1998.
[78] Pinker,
A., Smith, D., Walker, D., “Jamming the GPS Signal,”
Proceedings of the 55th Annual Meeting of the ION, Cambridge, MA,
28-30 June 1999.
[79] Littlepage,
R. S., “The Impact of Interference on Civil GPS,”
Proceedings of the 55th Annual Meeting of the ION, Cambridge, MA,
28-30 June 1999. (He warned us early on! His presentation
was more explicit than his paper. He was truly concerned.)
[80] Goldstein,
J. S., “Multistage partially adaptive STAP CFAR detection algorithm,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 35, No. 2,
pp. 645-669, April 1999.
[81]
Saha, R. K., “Effect of Common Process Noise on Two-Sensor Track
Fusion,” AIAA Journal of
Guidance, Control, and Dynamics, Vol. 19, No. 4, pp. 829-835, July-August
1996.
[82]
Fitzgerald, R. J., “Effects of Range-Doppler Coupling on Chirp
Radar Tracking Accuracy,” IEEE
Transactions on Aerospace and Electronic Systems, Vol. AES-10, No. 4, pp.
528-532, July 1974.
[83]
Brennan, L. E., Reed, I. S., “Theory of Adaptive Radar,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 9, No., pp.
237-252, March 1973.
[84] Brennan,
L. E., Mallett, J. D., Reed, I. S., “Adaptive Arrays in Airborne MTI Radar,”
IEEE Trans. on Antennas and Propagation, Vol. 24, No. 5, pp.
607-615, September 1978.
[85] Arregui, F. J. (ed.), Sensors Based on Nanostructured
Materials, Springer Science & Business Media LLC, 2009.
[86] Righini,
G. C., Tajani, A., Cutolo, A., An Introduction to Optoelectronic Sensors,
World Scientific, NY, 2009.
[87] Vladimir Cherkassky and Filip Mulier, Learning from
Data: Concepts, Theory, and Methods, John Wiley & Sons, Inc., NY, 1998.
[88] Gupta, S. N., “An Extension of Closed-Form Solutions
of Target-Tracking Filters with Discrete Measurements,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 20, No. 6, pp.
839-840, Nov. 1984.
[89] Junichiro Toriwaki, Hiroyuki Yoshida, Fundamentals of
Three-Dimensional Digital Processing, Springer-Verlag, London, 2009.
[90] Julien Bourgeois, Wolfgang Minker, Time-Domain
Beamforming and Blind Source Separation: Speech Input in the Car Environment,
Springer Science + Business Media, NY, 2009.
[91] Jekeli, C., “Navigation Error Analysis of Atom Interferometer Inertial
Sensing,”
Navigation: Journal of the Institute of Navigation, Vol. 52, No. 1, pp. 1-14, Spring 2005.
[92] Another intriguing wrinkle is conveyed in
Fernandez-Alcada, R., Navarro-Moreno, Ruiz-Molina, J. C., Oya, A., “Recursive
Linear Estimation for Doubly Stochastic Poisson Processes,” Proceedings of
the World Congress on Engineering (WCE), Vol. II, London, UK, pp. 2-6, 2-4
July 2007.
[93] Huddle, J.R., “Inertial Navigation System Error Model
Considerations in Kalman Filter Applications,” Control and Dynamic Systems:
Advances in Theory and Applications - Nonlinear and Kalman Filtering Techniques, Vol.
20, Academic Press, NY, pp. 294-340, Part 2 of 3, 1983.
[94] Lechner, W., “Application of Model Switching and
Adaptive Kalman Filtering for Aided Strapdown Navigation Systems,” Control
and Dynamic Systems: Advances in Theory and Applications - Nonlinear and Kalman
Filtering Techniques, Vol. 20, Academic Press, NY, pp. 155-185, Part 2 of 3,
1983.
[95] Chien, T. T., “An Adaptive Technique for a
Redundant-Sensor Navigation System,” Report No. T-560, C. S. Draper
Laboratory, Cambridge, MA, 1972.
[96] Salazar, M. R., “State Estimation of Ballistic
Trajectories with Angle-Only Measurements,” Control and Dynamic Systems:
Advances in Theory and Applications - Nonlinear and Kalman Filtering Techniques, Vol.
21, Academic Press, NY, pp. 117-175, Part 3 of 3, 1984.
[97] Hsiao, C.- Y., “Computational Techniques in Angle-Only
Tracking Filtering,” Control and Dynamic Systems: Advances in Theory and
Applications - Nonlinear and Kalman Filtering Techniques, Vol. 29, Academic
Press, NY, pp. 101-134, Part 2 of 3, 1988.
[98] Liang, D. F., “Comparisons of Nonlinear Recursive
Filters for Systems with Non-negligible Nonlinearities,” Control and
Dynamic Systems: Advances in Theory and Applications - Nonlinear and Kalman
Filtering Techniques, Vol. 20, Academic Press, NY, pp. 341-402, Part 2 of 3,
1983.
[99] Yannis A. Phillis, “Algorithms for Systems with
Multiplicative Noise,” Control and Dynamic Systems: Advances in Theory and
Applications - Nonlinear and Kalman Filtering Techniques, Vol. 30, Academic
Press, NY, pp. 65-83, Part 3 of 3, 1989.
[100] Yannis A. Phillis and Vassilis S. Kouikoglou, “Minimax
Estimation and Control of Multiplicative Systems,” Control and Dynamic
Systems: Advances in Theory and Applications - Nonlinear and Kalman Filtering
Techniques, Vol. 31, Academic Press, NY, pp. 93-124, Part 1 of 3, 1989.
[101] Ahn, B.-H., Regan, R., et al, “Inertial Technology
for the Future,” IEEE Trans. on Aerospace and Electronic Systems, Vol. 20, No.
4, pp. 414-444, Jul. 1984.
[102] Jayawardhana, B., Logemann, H., and Ryan, E. P., “The
Circle Criterion and Input-to-State Stability: new perspectives on a classical
result,” IEEE Control System Magazine, pp. 32-67, Vol. 31, No. 4,
August 2011.
[103] Yan, J., Hoag, J. B., Hindman, R. E., Bernstein, D.
S., “Longitudinal Aircraft Dynamics and the Instantaneous Acceleration
Center of Rotation: the case of the vanishing zeros,” IEEE Control System
Magazine, pp. 68-92, Vol. 31, No. 4, August 2011.
[104] Bergin, J., Guerci, J. R., MIMO Radar: Theory and
Practice, Artech House, Boston, 2018.
[105] Son, J. S., Thomas, G., Flores, B. C., Range-Doppler
Radar Imaging and Motion Compensation, Artech House, Boston, 2001.
[106] Guerci, J. R., Space-Time Adaptive Processing for
Radar, Artech House, Boston, 2003.
[107] Hudson, J. E., Adaptive Array Principles, Peter
Peregrinus, Ltd., London, U. K., 1981, reprinted 1989, 1991.
[108] Copps, E. M., “An aspect of the role of the clock in a GPS
receiver,” Navigation, Journal of The (U.S.) Institute of Navigation, Vol. 31, No. 3, pp.
233-242, 1986. Also in Global Positioning System, papers published in Navigation, reprinted by
The (U.S.) Institute of Navigation, Vol. III, pp. 44-53,
1986.
[109] Copps, E. M., Geier, G. J., Fidler, W. C. and Grundy, P. A.
, “Optimal processing of GPS signals,” Proceedings of the Thirty-Sixth Annual Meeting of The
(U.S.) Institute of Navigation, Monterey, CA, 23- 26 June, pp. 17-24,
1980. Also in Navigation, Journal of The (U.S.) Institute of Navigation, Vol. 27, No. 3, pp.
171-182, 1984. Also in Global Positioning System, papers published in Navigation, reprinted by
The Institute of Navigation, Vol. II, pp. 13-24, 1984. (cf.,
[178])
[110] Kashyap,
S. K., Naidu, V. P. S., Singh, J., Girija, G., Rao, J. R., “Tracking of Multiple Targets Using Interactive Multiple Model and Data Association
Filter,” Journal of Aerospace Science and Technologies, Vol. 58, No. 1, pp.
66-74, 2006.
NAVIGATION via Visual Cues Using Only Imaging Sensors:
[111] Rodriguez, J. J., Aggarwal, J. K., “Matching Aerial Images to 3D Terrain Maps,”
IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol. 12, No. 12, pp. 1138-1149, Dec. 1990:
Sparse terrain profile data are stored onboard and direct measurement of relative shifts between images are used to estimate position and velocity; however, an EKF is deemed superior here to use of merely a Kalman filter that uses altitude estimates in order to estimate aircraft position and velocity.
[112] Heeger, D. J., Jepson, A. D., “Subspace Methods for Recovering Rigid Motion I: Algorithm and Implementation,”
International Journal of Computer Vision, Vol. 7, No. 2, pp. 95-117, Jan. 1992:
Terrain matching methods are also used to estimate platform position and orientation via comparisons to an on-board digital elevation map.
[113] Soatto, S., Frezza, R., Perona, P., “Motion Estimation via Dynamic Vision,”
IEEE Trans. on Automatic Control, Vol. 41, No. 3, pp. 95-117, Mar. 1996:
A least squares formulation is used to recover user's 3D motion (3 translation variables and 6 rotation variables or 4 if quaternions are utilized).
[114] Goyurfil, P., Rotstein, H., “Partial Aircraft State Estimation from Visual Motion Using the Substate Constraint Approach,”
AIAA Journal of Guidance, Control, and Dynamics, Vol. 24, No. 5, pp. 1016-1025, Sep.-Oct. 2001:
What is called an implicit EKF is used here to estimate aircraft states-aircraft velocities, angular rates, angle of attack, and angle of sideslip but not aircraft Euler angles nor inertial location. Measurements available are the image points of N featured objects, which are tracked from one frame to another.
[115] Hoshizaki, T., Andrisani, D., Braun, A. W., Mulyana, A. K., and Bethel, J. S., “Performance of Integrated Electro-Optical Navigation Systems,”
Navigation: Journal of the Institute of Navigation, Vol. 51, No. 2, pp. 101-122, Summer 2004:
Contains good modeling and they have a “tightly coupled system consisting of INS, GPS, and EO” all working together to simultaneously benefit both navigation and photogrammetry (estimates platform states, sensor biases, and unknown ground object coordinates using a single Kalman filter).Use of control points avoided pre-stored terrain.
[116] Kyungsuk Lee, Jason M. Kriesel, Nahum Gat, “Autonomous Airborne Video-Aided
Navigation,” Navigation: Journal of the Institute of Navigation, Vol. 57, No. 3, pp. 163-173, Fall 2010:
ONR-funded discussion utilizes (1) “digitally stored georeferenced landmark images” (altimeter/DTED), (2) video from an onboard camera, and (3) data from an IMU. Relative position and motion are tracked by comparing simple mathematical representations of consecutive video frames. A single image frame is periodically compared to a landmark image to determine absolute position and to correct for possible drift or bias in calculating the relative motion.
[117] Craig Lawson, John F. Raquet, Michael J. Veth, “The Impact of Attitude on Image-Based Integrity,”
Navigation: Journal of the Institute of Navigation, Vol. 57, No. 4, pp. 249-292, Winter 2010:
Being aware of the historical importance of having good satellite geometry when seeking to utilize GPS for positioning and for timing (characterized by HDOP, VDOP, TDOP, and GDOP), they analogously extrapolate these ideas to the geometry of their airborne image collecting and refer to this as image integrity (similar to how researchers endeavor to associate sufficient Integrity to GPS measurements). Known a/c attitude significantly beats unknown attitude (altitude-indexed).
Also see: [159] by Dennis Milbert further below.
Likely comparable Classified DoD Pointing Improvements: Cobra Ball/Cobra Eye &
other airborne Laser developments.
Rigorous updates in airborne estimation for attitude determination:
[118] Crassidis, J. L., Markley, F. L., Cheng, Y., “Survey of Nonlinear Attitude Estimation Methods,”
Journal of Guidance, Control, and Dynamics, Vol. 30, No. 1, pp. 12-28, Jan. 2007:
An excellent survey on the subject of attitude estimation. It provides insights into what is important in estimation algorithms. It is a more practical and rigorous addendum to their many earlier surveys, concerned with utilizing alternative EKF's or Nonlinear Luenberger Observers (as alternatives to Extended Kalman filter-based approaches). They admonish to “stick with
EKF”.
[119] Majji, M., Junkins, J. L., Turner, J. D., “Jth Moment Extended Kalman Filtering for Estimation of Nonlinear Dynamic Systems,”
AIAA Guidance, Navigation, and Control Conference and Exhibit, Honolulu, HI, Paper No. AIAA 2008-7386, pp. 1-18, 18-21 Aug. 2008:
Explores two variations on JMEKF formulations that properly handle higher order moments (that lurk in the background while trying to get good estimates and covariances from EKF’s). Approximations utilized are acknowledged and properly handled (rather than ignored, as is usually the case). Errors reduced by several orders of magnitude within 5 sec., but results in normalized units (for comparisons to ordinary EKF approach, which it beat by a wide margin). Down side is its larger CPU burden yet to be completely quantified.
[120] Scorse, W. T., Crassidis, A. L., “Robust Longitudinal and transverse Rate Gyro Bias Estimation for Precise Pitch and Roll Attitude Estimation in Highly Dynamic Operating Environments Utilizing a Two Dimensional Accelerometer Array,”
AIAA Atmospheric Flight Mechanics Conference, Paper No. AIAA 2011-6447, Portland, OR, pp. 1-28, 8-11 Aug. 2011: Using the latest in rigorous real-time estimation algorithms (neither a particle filter nor an unscented/Oxford /Sigma-Point filter) for enabling accurate pointing (precise pitch and roll) within an aircraft within a high dynamics operating environment is reported. While it does utilize rate integrating
gyros. It also utilizes 2D accelerometer arrays and compares to an onboard gravity map to achieve its accuracy. Following reasonably large offsets, got back to within 0.1 degree pointing error within 10 seconds but results much worse with turbulence present.
[121] Jensen, Kenneth J., “Generalized Nonlinear Complementary Attitude Filter,”
AIAA Journal of Guidance, Control, and Dynamics, Vol. 34, No. 5, pp. 1588-1593 , Sept.-Oct. 2011:
Achieves a big breakthrough by providing a proof of this particular EKF’s global stability as a consequence
and now states that it possesses “almost” global asymptotic stability; however, the term “almost” is required terminology to keep probability theorists and purists happy with the wording of his claim. Author Jensen attains his results by utilizing appropriate stochastic Lyapunov functions (proper handling of such
is due to Prof. Emeritus Harold J. Kushner, Brown Univ.). I don’t know whether Jensen was the first to achieve this
new result?
[122] La Scala, B. F., Bitmead, R. R., James, M. R., “Conditions for stability of the Extended Kalman Filter and their application to the frequency tracking problem,”
Math. Control, Signals Syst. (MCSS), vol. 8, No. 1, pp. 1-26, Mar. 1995:
Proof of Stability for yet another EKF. Now worries about EFK divergence evaporate for this application.
[123] Reif, K., Gunther, S., Yaz, E., Unbehauen, R., “Stochastic stability of the continuous-time extended Kalman filter,”
Proc. Inst. Elect. Eng., Vol. 147, p. 45, 2000: Proof of Stability for yet another EKF. Now worries about EFK divergence evaporate for this
application.
[124] Salcudean, S., “A globally convergent angular velocity observer for rigid body motion,”
IEEE Trans. on Autom. Control, Vol. 36, No. 12, pp.1493-1497, Dec. 1991:
Proof of Stability for Luenberger Observer use too (~EKF).
Rigorous Matrix Kalman
Filter (MKF) updates in airborne estimation for attitude determination
(Cont.’d):
In anticipation of later success, I have explored some possibilities offered by
the following novel Kalman filter variants that use matrix sensor (allowing simultaneous angle) measurements in lieu of
the more familiar version of a Kalman filter involving only vector sensor (one-direction-at-a-time) measurements.
(JTIDS RelNav used multilateration and only ordinary
Kalman filters with vector sensors on each platform but had many participants in the net
who automatically responded at regular short intervals!)
[125] Choukroun, D., Weiss, H., Bar-Itzhack, I. Y., Oshman, “Kalman Filtering for Matrix Estimation,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 42, No. 1, pp. 147-159, Jan. 2006: A linear Matrix Kalman filter for DCM.
DCM Refinement #1
[126] Choukroun, D., Weiss, H., Bar-Itzhack, I. Y., Oshman, “Direction Cosine Matrix Estimation from Vector Observations Using a Matrix Kalman Filter,”
AIAA Guidance, Navigation, and Control Conference and Exhibit, pp. 1-11, Aug. 2003: A linear Matrix Kalman Filter for DMC using either vector or matrix measurement updates.
DCM Refinement #2 .
[127] Choukroun, D., “A Novel Quaternion Kalman Filter using GPS Measurements,”
Proceedings of ION GPS, Portland, OR, pp. 1117-1128, 24-27 Sep. 2002: An alternative
viewpoint: Quaternion Refinement #1.
[128] Choukroun, D., Weiss, H., Bar-Itzhack, I. Y., Oshman, “Kalman Filtering for Matrix Estimation,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 42, No. 1, pp. 147-159, Jan. 2006:
Quaternion Refinement #2.
[129] Choukroun, D., Bar-Itzhack, I. Y., Oshman, “Novel Quaternion Kalman Filter,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 42, No. 1, pp. 174-190, Jan. 2006:
Quaternion Refinement #3.
[130] Choukroun, D., Weiss, H., Bar-Itzhack, I. Y., Oshman, “Direction Cosine Matrix Estimation From Vector Observations Using A Matrix Kalman Filter,”
Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, pp. 1-11, 11-14 August 2003:
DCM Refinement #3
[131] Choukroun, D., “Ito Stochastic Modeling for Attitude Quarternion Filtering,”
Proceedings of Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control
Conference, Shanghai, P. R. China, pp. 733-738, 16-18 Dec. 2009: Quaternion Refinement #4.
In the above, DCM =
Direction Cosine
Matrix; and
for the Quaterion Matrices, the quaterions are to be normalized. One can convert
from quaternions to DCM and vice versa. For the Matrix KF material, above,
a major contributor was Daniel Choukroun, B. S. (Summa cum Laude), M.S., Ph.D. (1997, 2000, 2003), post-doc (UCLA), currently an Assistant Professor at Delft University of Technology, Netherlands.
In Thomas H. Kerr III's humble opinion,
Angle Only
Tracking (AOT) can
also be accommodated within the above structure by updating from two (or more) different
time-synchronized (via sorted time-tags) noncolocated sensors (with lever arms
appropriately accounted for) simultaneously (thus used as a matrix measurement). The optimal estimator retains a linear syructure and is finite dimensional. This is the benefit of this novel approach.
NASA updates in Spaceborne estimation for attitude determination:
[132] Cheng, Y., Landis Markley, F., Crassidis, J. L. Oshman, Y., “Averaging Quaternions,”
Advances in the Astronautical Sciences series, Vol. 127, American Astronautical Society, AAS paper No. 07-213, 2007:
Will eventually Summarize!
[133] Landis Markley, F., “Attitude Filtering on SO(3),” Advances in the Astronautical Sciences
series, Vol. 122, American Astronautical Society, AAS paper No. 06-460, 2006:
Will eventually Summarize!
[134] Cheng, Y., Crassidis, J. L., and Landis Markley, F., “Attitude Estimation for Large Field-of-View Sensors,”
Advances in the Astronautical Sciences series, Vol. 122, American Astronautical Society, AAS paper No. 06-462, 2006:
Will eventually Summarize!
[135] Landis Markley, F., “Attitude Estimation or Quaternion Estimation?,”
Advances in the Astronautical Sciences series, Vol. 115, American Astronautical Society, AAS paper No. 03-264, 2003:
Critical and thorough Analysis of 3 different EKF’s vs. Technion MKF. MKF
was ultimately improved by this investigation.
[136] Reynolds, R., Landis Markley, F., Crassidis, J. L., “Asymptotically Optimal Attitude and Rate Bias Estimation with Guaranteed Convergence,”
Advances in the Astronautical Sciences series, Vol. 132, American Astronautical Society, AAS paper No. 08-286,
2008: Will eventually Summarize!
Estimation Results for Bilinear Systems (to tie into the MKF results above):
[137] Halawani, T. U., Mohler, R. R., and Kolodziej, W. J., “A two-step bilinear filtering algorithm,”
IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 32, 344-352, 1984:
Will eventually Summarize!
[138] Glielmo, L., Marino, P., Setola, R., Vasca, F., “Parallel Kalman Filter Algorithm for State Estimation in Bilinear Systems,”
Proceedings of the 33rd Conference on Decision and Control, Lake Buena Vista, FL, pp. 1228-1229, Dec. 1994:
Will eventually Summarize!
[139] Wang, Z., Qiao, H., “Robust Filtering for Bilinear Uncertain Stochastic Discrete-Time Systems,”
IEEE Trans. on Signal Processing, Vol. 50, No. 3, pp. 560-567, Mar. 2002:
In general, “Robust” approaches usually have a sluggish
response time.
[140]] Lopes dos Santos, P., Ramos, J. A., Frias, R., “Derivation of a Bilinear Kalman Filter with Autocorrelated Inputs,”
Proceedings of the 46th Conference on Decision and Control, New Orleans, LA, pp, 6196-6202, 12-14 Dec. 2007:
Structure similar to what above Technion MKF exhibits.
While linear systems are very tractable, general nonlinear systems are less so. Bilinear systems are close to being linear systems and so are
somewhat more tractable, and likewise for their associated Optimal estimators.
Prof. Roger W. Brockett (Harvard-Emeritus) discusses how to handle bilinear systems in:
[141] Brockett, R. W., "Finite Dimensional Linear Systems," SIAM Classics in Applied Mathematics, 2015
(original in 1970).
We can provide 17 more examples of practical estimators for bilinear
systems, as have been reported in the technical literature by others over the
last 40+ years, (some involving Lie Algebras and Lie Brackets such as those
provided by
A. S. Willsky and J. T.-H. Lo for SO(2) and by many others later).
[142]
[143] S. Blackman and R. Popoli, Design and Analysis of Modern Tracking
Systems, Artech House, Boston, MA, 1999.
[144] B. D. Tapley, M. M. Watkins, J. C. Ries, G. W. Davis, R. J. Eanes, S. R. Poole, H. J. Rim, B. E. Schutz, and C. K.
Shum, “The joint gravity model 3,” Journal of Geophysical Research,
Vol. 101, No. B12, pp. 28 029–28 049, Dec. 1996.
[145] N. Bergman, “Recursive Bayesian estimation: Navigation and tracking applications,” Ph.D. dissertation, Linkoping
University, SE-581 83 Linkoping, Sweden, April 1999.
[146] N. Bergman, Sequential Monte Carlo Methods in
Practice, New York: Springer, New York, 2001 (Chapter: Posterior
Cramér-Rao
Bounds for Sequential Estimation, pp. 321–338).
[147] Vytas B. Gylys, Kalman Filters and Nonlinear
Filters, Texas Instruments Inc.
[148] Wasim Huleihel, Joseph Tabrikian, and Reuven Shavit, “Optimal Adaptive Waveform Design for Cognitive MIMO
Radar,”
IEEE Transactions on Signal Processing, Vol., 61, No. 20, pp. 5075-, Oct. 2013.
[Assumes fixed, known target range and Doppler information and only in the
conclusion do they sketch how it may, perhaps, be successfully extended to a more realistic situation where the target is actually moving with respect to the
radar. Did anyone actually follow-up to see whether it actually resolves as they speculated? No wonder
Dr. Eli Brookner is “up in arms” about MIMO practitioners either doing what can already be done conventionally or about overstepping or overstating what MIMO can actually
do! Perhaps benefits of MIMO in communications applications are better
justified.]
http://www.ee.bgu.ac.il/~rshavit/Papers/p52.pdf
[149] M. Morf, J.R. Dobbins, B. Friedlander, T. Kailath, “Square-root algorithms for
parallel processing in optimal estimation,” Automatica,
Vol. 15, No. 3, pp. 299-306, 1979.
[150] H. H. Afshari, S. A. Gadsden, S. Habbi, “Gaussian Filters for parameter and state estimation: a general review of the theory and recent
trends,” Signal Processing, Vol. 135, pp. 218-238, 2017.
[151] http://www.gallup.unm.edu/~smarandache/NATOASI_ATJDTSPK.pdf
[152] F. Landis Markley, John L. Crassidis, Yang Cheng, “Nonlinear Attitude Filtering
Methods,” American Institute of Aeronautics and Astronautics, pp. 1-32,
2007. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20050212421.pdf
Landis.Markley@nasa.gov AIAA Fellow
I. Introduction
(from the above [152], and copied
verbatim, as follows next)
The extended Kalman (EKF) is the workhorse of real-time spacecraft attitude estimation. Since the group SO(3) of rotation matrices has dimension three, most attitude determination EKFs use lower-dimensional attitude parameterizations than the nine-parameter attitude matrix itself. The fact that all three-parameter representations of SO(3) are singular or discontinuous for certain
attitudes has led to extended discussions of constraints and attitude representations in EKF
& 719-11 These issues are now well understood, however, and the EKF, especially in the form known as the multiplicative extended Kalman filter5-7 (MEKF), has performed admirably in the vast majority of attitude determination applications.
Nevertheless, poor performance or even divergence arising from the linearization implicit in the EKF has led to the development of other filters. Several of these approaches retain the basic structure of the EKF, such as additive EKF a backwards-smoothing EKF,l8 and deterministic EKF-like estimators. ”-” In particular, the backwards-smoothing EKF solves a nonlinear smoothing problem for the current and past sample intervals using iterative numerical techniques. The numerical iteration retains all of the
nonlinearities of a fixed number of stages that precede the terminal stage of interest, and it processes information from earlier stages in an approximate manner. l5 Deterministic EKF-like estimators are closely related to
H_infinity control design.” Usually an upper bound is derived first, and then the bound is minimized based on approaches such as Riccati equations and linear matrix inequalities. The nonlinear problem is much more
difficult; which requires the solution of the Hamilton-Jacobi-Isaacs partial differential inequality. For attitude estimation, small-error approximations are used to developed a filter. 19i20 Other designs use various assumptions to derive simplified filters. These generally provide suboptimal performance characteristics in relation to the EKF, but involve linear or pseudo-linear equations that are used to estimate the states of a nonlinear dynamical system. Therefore, linear design and analysis tools can be used to construct the filter and
to assess its overall performance. Some of these use a deterministic solution of the attitude] e.g. methods that are based on the QUEST attitude determination solution.23 Simple filter designs based on QUEST include filter QUEST24 and recursive QUEST.25 A more complicated but far more robust approach] called extended uses a full nonlinear propagation along with a novel measurement update. This approach can be used to estimate attitude and additional parameters as well. Interlaced filters that replace a nonlinear filter with two or more linear filters have been used for rate estimation] but not for attitude e~timation.~~-~’ Several new alternatives to the standard EKF have been recently introduced] such as sigma point or unscented filter^^'-^^ and particle filter^.^^-^^ Unscented filters (UFs) have been shown to exhibit several advantages over the EKF, including: 1) the expected error is lower than the EKF, 2) they can be applied to non-differentiable functions, 3) no Jacobian matrix calculations are required] and 4) they provide higher- order expansions than the standard EKF. Unscented filters work on the premise that with a fixed number of parameters it should be easier to approximate a Gaussian distribution than to approximate an arbitrary nonlinear function. They typically use the standard Kalman form in the post-update, but use a different propagation of the covariance and pre-measurement update with no local iterations. The attitude
estimation UF derived in Ref. 33 is based on a quaternion representation of the attitude kinematics. However, straightforward implementation of the standard UF equations derives a predicted quaternion mean from an averaged sum of quaternions. Therefore, no guarantees can be made that the resulting quaternion will have unit norm. This was overcome by using a generalized unconstrained three-component vector to represent the attitude error-quaternion] leading to an unconstrained formulation in the UF design. Unscented filters are essentially based on second or higher order approximations of nonlinear functions, which are used to estimate the mean and covariance of the state vector. Though the mean and covariance are the sufficient statistics of a Gaussian distribution, they are not sufficient to represent a general probability distribution. When UF methods are applied to strongly nonlinear and non-Gaussian estimation problems] where the a
posteriori distribution of the state vector may be multi-peaked, heavily-tailed, or skewed, desired performance characteristics may not be obtained. This may be overcome by using particle filter^^^-^^ (PFs). Like other approximate approaches to optimal filtering] the ultimate objective of PFs is to construct the a posteriori probability density function (PDF) of the state vector, or the PDF of the state vector conditional on all the available measurements. However, the approximation of PFs is vastly different from that of
conventional nonlinear filters. The central idea of a PF approximation is to represent a continuous distribution of interest by a finite (but large) number of weighted random samples of the state vector, or particles. A PF does not assume the a posteriori distribution of the state vector to be a Gaussian distribution or any other distribution of known form. In
principle,it can estimate probability distributions of arbitrary form and solve any nonlinear and/or non-Gaussian system. Reference 36 presents a PF for attitude estimation based on the bootstrap filter.35 The optimal solution of the nonlinear estimation problem requires the propagation of the conditional PDF of the state given the observation history.37 All practical nonlinear filters are approximations to this ideal. Exact finite dimensional filters38 can be found that solve some nonlinear problems by using the Fokker-Planck equation2l3’ to propagate a non-Gaussian PDF between measurements and Bayes’ formula‘? to incorporate measurement information. A recently proposed filter4’ follows this pattern, but does not solve the nonlinear attitude filtering problem exactly. We refer to it as an orthogonal filter, because it represents the attitude by an orthogonal rotation matrix, rather than by some parameterization of the rotation matrix. The PDF is a non-Gaussian function defined on the Cartesian product of S0(3), the group of rotation matrices, and the Euclidean space
Rn of bias parameters. This filter entirely avoids questions about singularities of representations or covariance matrices arising in EKFS~-~~ and UFS,~~ and has the additional advantage of providing a consistent initialization for a completely unknown initial attitude, owing to the fact that SO(3) is a compact space. Nonlinear observers often exhibit global convergence, which is to say that they can converge from any initial guess.41 Several applications of observers for attitude control have been proposed Refs. 42-48. A nonlinear observer and controller using only measurements of roll, pitch and yaw has been developed in Ref. 43. Local asymptotic stability is ensured under mild hypotheses. A globally convergent, nonlinear full- order observer using quaternions and Euler’s equations for the dynamics has been derived in Ref. 44. The observer structure contains a discontinuous term, which is often associated with “sliding mode” observers. The error-quaternion is defined using a multiplicative approach and stability is proven using a Lyapunov function. A simpler, robust smoothed sliding mode observer that avoids quaternion error differentiation noise and eliminates the necessity of measuring angular rate is derived in Ref. 45. Although an additive approach is used to define the quaternion error, global stability is still provided through a Lyapunov function. Algrain and Lee develop a nonlinear observer to estimate angular rates along the third axis of a spinning spacecraft using only two-axis measurement^.^^ A pseudo-linear model is developed by decomposing the nonlinear system into linear and nonlinear parts. BoSkoviC, Li and Mehra use angular rate measurements with quaternion kinematics to derive a nonlinear bias observer, which is coupled with an adaptive sliding mode ~ontroller.~~ Stability is proven as long as the attitude never passes through f180 rotations. Thienel and Sanner develop an exponentially convergent nonlinear observer given a constant gyro bias with identification of the bias proven through a persistency of excitation argument.48 An analysis is also shown that includes gyro noise. Adaptive approaches generally fall into two categories. One category encompasses approaches that adap- tively tune the Kalman filter through the identification of either the process noise covariance or measurement noise covariance, or both simultaneously. In practice “tuning” a Kalman filter can be arduous and very time- consuming. Usually, the measurement-error covariance is fairly well known, derived from statistical inferences of the hardware sensing device. However, the process noise covariance is usually not well known and is of- ten derived from experiences gained by the design engineer based on intimate knowledge of the particular system. The approach is based on “residual whitening.” 49 Unfortunately, most noise adaptive techniques are applicable only for linear systems,’ which creates problems for attitude estimation due to the nonlinear equations involved. Still, it is possible to use these techniques with linearized equations, as demonstrated in Ref. 50. Lam and Wu further develop adaptive filters that address both colored and white noise ~tatistics.~~ The former noise is identified using a non-parametric neural network approach, while the latter noise is identified using an a-P filter. An adaptive filter is also proposed in Ref. 17 to account for inaccuracy in the knowledge of the process noise statistical model, which uses a linear pseudo-measurement model. Other adaptive approaches use adaptive methods for fault tolerant estimation 53 The other category includes approaches that adaptively estimate unknown system parameters, such as the inertia matrix. These generally fall into two basic categories: 1) parameter estimation or filter-based methods, and 2) nonlinear adaptive techniques. Least squares methods to determine the inertia matrix and other constant parameters, such as disturbance model parameters and biases, are shown in Refs. 54-56. A disturbance accommodation technique that models the unknown disturbance angular rate using a power set of time as basis functions is shown in Ref. 57. Nonlinear adaptive techniques are similar to nonlinear observers in that they usually provide global stability proofs that guarantee convergence of the estimated parameter^.^^-^' This paper will review the basic assumptions of these filters, presenting enough mathematical detail to give a general orientation. First, reviews of the quaternion parameterization and gyro model equations are given. Then, attitude estimation methods based on the EKF are shown, followed by QUEST-based approaches. Next, the two-step estimator is shown. The UF and PF approaches are then shown, followed by the orthogonal filter. Then, the predictive filter, as well as nonlinear observers and adaptive approaches are reviewed. The paper concludes with a discussion of the strengths and weaknesses of the
various filters. (Thomas H. Kerr comment: Also
see item [168] below for a 1971 precedent for handling estimation on a circle,
SO(2), and on a sphere, SO(3).)
Other topics that I routinely follow:
[153] Niu, X., Nassar, S., El-Sheimy, N., “An Accurate Land-Vehicle MEMS IMU/GPS Navigation System Using 2D Auxiliary Velocity
Updates,” Navigation: Journal of the Institute of Navigation, Vol. 54, No. 3, pp. 177-188, Fall 2007.
[154] Soloviev, A., van Graas, F., “Batch-Processing of Inertial Measurements for Mitigation of Sculling and Commutation
Errors,” Navigation: Journal of the Institute of Navigation, Vol. 54, No. 4, pp. 265-276, Winter 2007.
[155] Soloviev, A., van Graas, F., “Enhancement of Integrated GPS/INS Performance Utilizing Frequency Domain Implementation of INS
Calibration,” Navigation: Journal of the Institute of Navigation, Vol. 54, No. 2, pp. 87-98, Summer 2007.
[156] Lee, Y. C., “Two New RAIM Methods Based on the Optimally Weighted Average Solution (OWAS)
Concept,” Navigation: Journal of the Institute of Navigation, Vol. 54, No. 4, ff. 333, Winter 2007.
[157] Farrell, J. L., “Inertial Instrument Error Characterization,” Navigation: Journal of the Institute of
Navigation, Vol. 54, No. 3, pp. 169-176, Fall 2007.
[158] Farrell, J. L., “Full Integrity Testing for GPS/INS,” Navigation: Journal of the Institute of
Navigation, Vol. 53, No. 1, pp. 33-40, Spring 2006.
[159] Milbert, D., “Dilution of Precision Revisited,” Navigation: Journal of the Institute of
Navigation, Vol. 55, No. 1, pp. 67-81, Spring 2008.
[160] Pulford, G. W., “A Proof of the Spherically Symmetric Overbounding Theorem for Linear
Systems,” Navigation: Journal of the Institute of Navigation, Vol. 55, No. 4, pp. 283-292, Winter 2008.
[161] Li, Y., Rizos, C., Wang, J., Mumford, P., Ding, W., “Sigma-Point Kalman Filtering for Tightly Coupled GPS/INS Integration,” Navigation: Journal of the Institute of
Navigation, Vol. 55, No. 3, pp. 167-177, Fall 2008.
[162] “Algorithm Aligns Gyrocompass in Twisting and Swaying Vehicle,” NASA Tech Briefs
MFS-28671, George C. Marshall Space Flight Center, Alabama 35812, Gyrocompass FDR Version 6.0.6/MO (from Specification CP-830100A, Appendix 1, Rev. A, 28 July 1989 for TOS on Titan), pp. 1-87, 18 June 1991.
[163] Shively, C. A., Hsio, T. T., “Error and Availability Analysis of CAT IIIb LAAS Augmented by Radar
Altimetry,” Navigation: Journal of the Institute of Navigation, Vol. 52, No. 3, pp. 155-162, Fall 2005.
[164] Mason, J., “Algebraic Two-Satellite TOA/FOA Position Solution on an Ellipsoidal
Earth,” IEEE Trans. on Aerospace and Electronic Systems, Vol. 40, No. 7, pp. 1087-1092, July 2004.
[165] Mason, J., Romero, L., “TOA/FOA Geolocation Solutions Using Multivariate Resultants,” Navigation: Journal of the Institute of
Navigation, Vol. 52, No. 3, pp. 163-177, Fall 2005.
[166] Jekeli, C., “Navigation Error Analysis of Atom Interferometer Inertial Sensing,” Navigation: Journal of the Institute of
Navigation, Vol. 52, No. 1, pp. 1-14, Spring 2005.
[167] Ristic, B., Arulampalam, S., Gordon, N., Beyond the Kalman Filter: Particle Filters for Tracking
Applications, Artech House, Boston, MA, 2004. [One of the clearest discussions of both historical and recent estimation algorithms (including
EKF, UKF, MMM, IMM, and Particle Filters), their underlying assumptions/mechanization equations and
that also provides extremely useful insight into important aspects and distinctions in their implementations is offered in Chapters
1-3.]
[168] Li, J. T.-H. Lo and A. S. Willsky, “Estimation for Rotational Processes with One Degree of Freedom-Part 1,”
IEEE Trans. on Automatic Control, Vol. 20, No. 1, pp. 10-21, Feb. 1975.
[They explicitly handle estimation on a circle, SO(2),
rather than estimation on a sphere, SO(3), as NASA's F. Landis Markley, et al deal with above in
their extensive survey and comparison between approaches and techniques in
[152].
However, Willsky and Lo are particularly lucid in their development and
exposition and, moreover, within the last sentence of their conclusion, provide specifics of their
suggested generalization to estimation results on arbitrary
Abelian Lie groups, such as SO(3).] 5_pub_IEEE.pdf
[169] Lo, J. T.-H. and Willsky, A. S., “Stochastic Control of Rotational Processes with One Degree of
Freedom,” SIAM Journal on Control, Vol. 13, No. 4, 886ff, July 1975.
[170] Patrick K. Simpson (Ed.), Neural Networks Theory,
Technology, and Applications, Selected Conference Papers, IEEE Technology
Update Series, NY, 1996.
[171] Jekeli, C., Inertial Navigation Systems with Geodetic Applications, Walter deGruyter GmbH \& Co. KG, Berlin, Ger., 2001.
For the following navigation textbooks:
[172] Rogers, R. M., Applied Mathematics in Integrated Navigation Systems, AIAA Education Series, AIAA, pp. 99-108, Reston, VA., 2000.
[173] Titterton, D. H., and J.L. Weston, Strapdown Inertial Navigation
Technology, Peter Peregrinus Ltd., Stevenage, Herts, England, UK, 2004.
[174 ] Farrell, J. A., Aided Navigation: GPS with High Rate Sensors, McGraw-Hill, NY,
2008 (very well written but uses lower case Greek epsilon in a role
that was NOT gyro drift-rates, contrary to the standard convention of the last 3
decades)
all three of these textbooks are not totally
self-contained but, instead, defer to the following textbook at exactly
the same point
in their discussions for completion of the proper handling of components of gyro drift-rate to be used in mathematical model
to be eventually used in the corresponding navigation Kalman filter,
as discussed in detail in:
[175] Kenneth R. Britting, Inertial Navigation Systems Analysis, Wiley-Interscience, NY, 1971.
[Surprisingly, a new edition of this book and its 2010
sequel are now available from Artech, Boston, MA. The reason that it is
surprising to me is that Kenneth R. Britting died from M.S. in the 1980's while
he was with Nortronics at Northrop in Norwood, MA. A burning question is whether
Fred J. Marcus is helping Kenneth R.
Britting to publish from the grave AGAIN?]
[176] Chatfield, A. B. (Ed.), Fundamentals of High Accuracy Inertial
Navigation, Paul Zarchan, Editor-in-Chief, AIAA Progress in Astronautics and Aeronautics Series, AIAA, 1997.
[177] Savage, P. G., “Strapdown Sculling Algorithm Design for Sensor Dynamic Amplitude and Phase-Shift
Error,” AIAA Journal of Guidance, Control, and Dynamics, Vol. 35, No. 6, pp. 1718-1729, Nov.-Dec. 2012.
[178] Jaewon
Seo,
Jang Gyu Lee, Chan Gook Park, “A New Error Compensation Scheme for INS
Vertical Channel,” IFAC Proceedings, Vol. 37, No. 6, pp. 1119-1124, 2004.
[179] Viterbi algorithm being equivalent to Dynamic Programming:
https://scholar.google.com/scholar?q=viterbi+algorithm+dynamic+programming&hl=en&as_sdt=0&as_vis=1&oi=scholart&sa=X&ved=0ahUKEwiwhOicsejaAhVGc98KHScLD1UQgQMIJTAA
[180] Uwe D.
Hanbeck, “Recursive Nonlinear Set-Theoretic Estimation Based on
Pseudo-Ellipsoids,” Proceedings of the IEEE Conference on Multisensor Fusion and Integration for Intelligent
Systems, pp. 159–164 (MFI’
2001), Baden–Baden
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.304.8080
https://www.researchgate.net/publication/3955109_Recursive_nonlinear_set-theoretic_estimation_based_on_pseudo_ellipsoids
https://core.ac.uk/display/22665895
https://core.ac.uk/display/24506648
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.70.3779
Their patent abandoned by Siemens AG (perhaps because of prior art: me): https://patents.google.com/patent/US20060234722A1/en
[181]
Fuqiang You, Hualu Zhang, Fuli Wang, “A new set-membership estimation method based on zonotopes and
ellipsoids,”
Transactions of the Institute of Measurement and Control, Vol. 40, issue 7, pp. 2091-2099, Article first published online:
27 July 2016; Issue published: 1 April 2018
[182] Grocholsky B., Stump E., Shiroma P.M., Kumar V., “Control for Localization of Targets Using Range-Only
Sensors,” in Khatib, O., Kumar, V., Rus, D.
(eds), Experimental Robotics, Springer Tracts in Advanced Robotics
Series, Vol 39. Springer, Berlin, Heidelberg, pp. 191-200, 2008.
[183] Ashok K. Rao, Yih-Fang Huang, and Soura Dasgupta, “ARMA Parameter Estimation Using a Novel Recursive Estimation Algorithm with Selective
Updating,”
IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 38,
No. 3, Mar. 1990.
https://www3.nd.edu/~huang/papers/IEEE-T-SP-Mar1990-RH.pdf
[184] Set Estimation: https://en.wikipedia.org/wiki/Set_estimation
[185]
Donald Cooke, Fun with GPS, ESRI Press, 380 New York St., Redlands, CA,
2005.
[186]
Quantum Navigation using magnetic sensing of gravity
anomalies to match known maps of such: https://www.wired.com/story/quantum-physicists-found-a-new-safer-way-to-navigate/
[187] Walking Robot uses the sun to navigate (and nothing else):
https://gizmodo.com/this-walking-robot-navigates-using-the-sun-no-gps-requ-1832599931
[188]
Jeffrey E. Hilland, F. B. Stuhr, A. Freeman, D. Imel, R. L. Jordan, E. R. Caro, “Future NASA Spaceborne SAR
Missions,” Systems Magazine, IEEE Aerospace and Electronic Systems,
Vol. 13, No. 11, pp. 9-16, Nov. 1998.
[189] Yaakov Bar-Shalom, and Xiao-Rong Li, “Multitarget-Multisensor Tracking: Principles and
Techniques,” Systems Magazine, IEEE Aerospace and Electronic Systems,
Vol. 11, No. 2, pp. 41-44, Feb. 1996.
[190]
B. Wu, P. Nicolaides, and T.N. Upadhyay,T.R. Jenkins, “IONOSPHERIC ERROR COMPENSATION FOR GPS RECEIVERS USING REAL-TIME IONOSPHERIC
MODEL,”
Proceedings of the 9th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1996), Kansas City, MO,
pp. 575-583,
[191]
Grewal, M. S., Weill, L. R., and Andrews, A. P.,
Global Positioning Systems, Inertial Navigation and Integration, John Wiley & Sons, Hoboken, NJ, 2007.
[192] Abbott, A. S., Lillo, W. E.,
Global Positioning Systems and Inertial Measuring Unit Ultratight Coupling
Method, U. S. Patent 6,516,021, 4 Feb. 2003.
[193] Kushner, H. J., Budhiraja, A. S.,
"A Nonlinear Filtering Algorithm Based on an Approximation of the Conditional Distribution,"
IEEE Trans. on Automatic Control, Vol. 45, No. 3, pp. 580-585, Mar. 2000.
[194] Landis, D., Thorvaldsen, T., Fink, B., Sherman, P., and Holmes, S.,
"A Deep Integration Estimator for Urban Ground Navigation," Proc. of IEEE PLANS
Conference, San Diego, 25-27 Apr. 2006.
[195] Bowles, W. M.,
Correlation Tracking, D. Sc. Thesis, Aero. and Astro. Dept., MIT, Cambridge, MA, Jun. 1980.
[196] Nunes, F., Sousa, F., and Leitao, J.,
"Innovations-Based Code Discriminator for GPS/Galileo BOC Signals," IEEE Vehicular Technology
Conference, pp. 4127-4131, Sept. 2004.
[197] Li, Y., Rizos, C., Wang, J., Mumford, P., and Ding,
"Sigma-Point Kalman Filtering for Tightly Coupled GPS/INS
Integration," Navigation, Journal of ION, Vol. 55, No. 3, Fall 2008.
[198]
Yannis A. Phillis and Vassilis S. Kouikoglou, "Algorithms for System Minimax Estimation and Control with Multiplicative Noise of Multiplicative System,"
Control and Dynamic Systems, Vol. 31: Advances in Aerospace Systems, Part 1, edited by C.T. Leonides, pp. 93-124, 2012.
[199] Weiwei Li, Emanuel Todorov, and Robert E. Skelton, "Estimation and Control of Systems with Multiplicative Noise via Linear Matrix Inequalities,"
Proceedings of the American Control Conference, Portland, OR, pp. 1811-1816, 8-10
June, 2005.
Abstract: This paper provides estimation and control design methods for linear discrete-time systems with multiplicative noise. First, we present the design of the state feedback controller, such that the closed loop system is mean square stable. Second, we provide sufficient conditions for the existence of the state estimator; these conditions are expressed in terms of linear matrix inequalities (LMIs), and the parametrization of all admissible solutions is addressed. Finally, an estimator design approach is formulated using
LMS, and the performance of the estimator is examined by means of numerical examples.
[200] Owen, A.B.,
Empirical Likelihood, CRC Press, 2001. (QA 276.8.094, Hayden, MIT).
[201] Huddle, J. R., "Inertial Navigation System Error Model Considerations in Kalman Filter Applications,"
Control and Dynamic Systems (Ed. C.T. Leondes) Vol. 20, Part 2, pp. 293-339, 1983.
[202]
Tam, P. K. S., and Moore, J. B., "A Gaussian Sum Approach to Phase and Frequency Estimation,"
IEEE Transactions on Communications, Vol. 25, No. 9, Sep 1977: https://scholar.google.com/scholar?lookup=0&q=%22A+Gaussian+Sum+Approach+to+Phase+and+Frequency+Estimation%22&hl=en&as_sdt=0,22&as_vis=1
Abstract: In this paper, a theory of optimal nonlinear estimation from sampled data signals where the a posteriori probability densities are approximated by Gaussian sums is adapted for application to phase and frequency estimation in high noise. The nonlinear estimators (demodulators) require parallel processing of the received signal. In the limit as the number of parallel processors becomes infinite the FM demodulators become optimum in a minimum mean square error sense and the PM demodulators become optimum in some well defined sense. For the clearly
sub-optimal case of one processor, the demodulators can be readily simplified to the familiar phase-locked loop. On the other hand, for the intermediate case, significant extension of the
phase-locked loop threshold is achieved where (say) six parallel processors are involved.
[203]
Raytheon-UTC merger wins approval, pending divestitures:
https://www.defensenews.com/industry/2020/03/27/raytheon-utc-look-to-shed-segments-to-win-merger-approval/
The Biggest Defense Merger Ever Gets Key Antitrust Approval — With These Conditions:
https://www.investors.com/news/united-technologies-raytheon-merger-approval-conditions/
US Coast Guard protests GPS disruption to UN body: ‘urgent issue’ - GPS World | RNTF:
https://rntfnd.org/2020/03/26/us-coast-guard-protests-gps-disruption-to-un-body-urgent-issue-gps-world/
https://rntfnd.org/wp-content/uploads/MSC-102-22-5-Interference-with-the-United-States-Global-Positioning-System-GPS-and-other-Global-Nav...-the-United-States.pdf
https://www.icao.int/Meetings/A40/Documents/WP/wp_188_en.pdfhttps://www.prnewswire.com/news-releases/raytheon-aerojet-rocketdyne-strike-1-billion-strategic-sourcing-deal-for-standard-missile-programs-301030437.html
[204]
GPS/JTIDS/INS Integration Study-Final Report, Vol. II of IV, Details, Technical Report Report R-1151, The Charles Stark Draper Laboratory, Inc., Cambridge, MA, Oct. 1977 to June 1978.
[205] John E. Bortz Jr.,
MICRON ANALYSIS, Vol. I: MESGA Attitude Readout Error, The Analytic Sciences Corporation, Technical Report AFAL-TR-72-22B, Vol. I, Aug. 1972.
[206]
Evatt, T. C., Failue Control Techniques for the SSME- Phase I Final Report, NAS8-36305, prepared for NASA Marshall Space Flight Center, Huntsville, AL, Rockwell International: Rocketdyne Division, TR RI/RD86-165, 1986.
[207] Cikanek III, H. A.,
"SSME Failure Detector," Proceedings of the American Control
Conference, pp. 282-286, 19-21 June 1985.
[208]
Ekstran, R., "Analytical Steady State Solution for a Kalman Tracking Filter," IEEE Trans. on Aerospace and Electronic
Systems, Vol. 19, No. 6, pp. 815-819, Nov. 1983.
[209] Spitzer, F.,
Random Fields and Interacting Particle Systems, Notes on Lectures given at the 1971 MAA Summer Seminar Williams College, Williamstown, MA, 1971.
[210]
Facklam, R. L., "Ultra-Stable Laser Clock," AFWAL-TR-83-1155, Final Report for Dec. 1981-Aug. 1983.
[211] Special Issue on Two-Dimensional Spectral Analysis,
Proceedings of the IEEE, Vol. 62, No. 10, Oct. 1974.
[212]
Gandell, J., Doubly Stochastic Poisson Processes, Lecture Notes in Mathematics, No. 529, Edited by A. Dold and R. Eckmann, Springer-Verlag, NY, 1976.
[213]
Wolovich, W. A., "On the numerators and zeros of rational transfer matrices," IEEE Trans. on
AC, pp. 544-545, Oct. 1973.
[214]
Widnall, W. S., Stability of Alternate Designs for Rate Aiding of Non-Coherent Mode of a GPS
Receiver, Technical Report IR-302, Intermetrics Inc., Cambridge, MA, 25 Sept. 1978.
[215]
Danik, B., "A low cost velocity system for rapid alignment of aircraft inertial platforms on a moving base,
Singer-Kearfott, pp.608-615, Proceedings of IEEE 1980 National Aerospace and Electronics Conference, NAECON, Vol. 1, 1980.
[216] Bryant, R. H., Graff, J. A., "In-flight Calibration and initialization of low cost inertial navigation systems," Boeing Aerospace Company, pp. 406-413, Proceedings of IEEE 1978 National Aerospace and Electronics Conference,
NAECON, 1978.
[217] Akira Ohsumi, Marc Mangel, "Joint Seaching and Parameter Identification for a Markovian Target,"
Proceedings of 1985 American Control Conference, Boston, MA, 19-21 June 1985.
[218] Y. Sunahara, A. Ohsumi, K. Terashima, H. Akashi, and Y. Takeuchi, "On
Lie Algebraic Solution of a Class of Vector Stochastic Differential Equations and its Application to Stability Analysis,"
10th JAACE Symposium on Stochastic Systems, Kyoto, Japan, pp. 17-20, 1978.
[219]
Hurras, K., Winter, H., "Gyro Accuracy Requirements in a Strap-Down INS with GPS Aiding for RPV Missions,"
[220] R. Baldassini Fontana, "Strapped Down Inertial Guidance System Study," AGARD-CP-116,
Proceedings of Guidance and Control Panel of AGARD, held in Florence, Italy, 2-5 Oct. 1972.
[221] Reid, J. G., Tucker, M., Dayan, R., "An Extended Kalman Filter for the Estimation of Transfer Alignment Errors to an Airborne Vehicle,"
AIAA Paper 80-1720, pp. 54-61, 1980.
[222]
Krogman, U. K., Advanced Procedures for Self-Alignment and Calibration of Inertial Platforms, pp. 21A-1 to 21C-15, AGARD-CP-116,
Proceedings of Guidance and Control Panel of AGARD, held in Florence, Italy, 2-5 Oct. 1972.
[223]
Bergeson, J. E., Witte, J. H., "Performance Comparison of Space Stable and Local Level Inertial Platform Mechanizations for a Strategic Aircraft Application,"
NAECON 75, pp. Record-617 to Record-624, 1975.
[224]
The Impact of Global Positioning System on Guidance and Control Systems Design of Military
Aircraft, Vol. IID, Specific Application Study No. 4: Stike RPV, AGARD-AR-147-VOL.
IID.
[225] Kuang-Chung Wei, "A class of Controllable Nonlinear Systems," Technical Notes and
Correspondence, IEEE Trans. on AC, pp. 787-789, Oct. 1976.
[226]
TASC Navigation Course: SLBM Fire Control & Guidance, 7-9 Oct. 1975. unclassified version, The Analytic Sciences Corp, Reading, MA, 1975.
[227]
Electrically Suspended Gyro Navigator AN/WSN-3A(V)2, NAVSEA 0924-LP-066-6010, July 1983
[228] Widnall, W. S. and Grundy, P. A.,
Doppler Velocity Sensor APN-200 Error Model and Flight Test Results, Intermetrics Technical Report TR-IR 78-74, Intermetrics, Inc., Cambridge, MA, 8 Mar. 1974.
[229]
Tranquilla, J. M., Carr, J. P., "GPS Multipath Field Observations at Land and Water Sites,"
Navigation: Journal of the Institute of Navigation, Vol. 37, No. 4, pp. 393-414, Winter 1990-1991.
[230] Ang Jr, M. H.,
Tourassis, V., ",Singularities of Euler and Roll-Pitch-Yaw Representations," IEEE Trans. on Aerospace and Electronic
Systems, Vol. 23, No. 3, pp. 317-324, May 1987.
[231] Astrom, K. J.,
"Computer Control of a Paper Machine--an Application of Linear Stocastic Control Theory,"
IBM Journal, pp. 389-405, July 1967.
[232] Mitter, S. K., and Moro, A. (Editors),
Nonlinear Filtering and Stochastic Control, No. 972, Springer-Verlag, NY, 1982.
[233] C Bendjaballah, "Time-interval distributions of a random point process in the detection of classical and nonclassical states of light,"
Journal of Optics B: Quantum and Semiclassical Optics, 10.1088/1464-4266/5/4/308, 5, 4, (370-375), (2003).
[234] A. J. Lawrance, "Arbitrary Event Initial Conditions for Branching Poisson Processes,"
Journal of the Royal Statistical Society: Series B (Methodological), 34, 1, (114-123), (2018).
Wiley Online Library
[235] M. R. Leadbetter, "On Streams of Events and Mixtures of Streams,"
Journal of the Royal Statistical Society: Series B (Methodological), 28, 1, (218-227), (2018).
Wiley Online Library
[236] Peter A. W. Lewis, "A Branching Poisson Process Model for the Analysis of Computer Failure Patterns,"
Journal of the Royal Statistical Society: Series B (Methodological), 26, 3, (398-441), (2018).
Wiley Online Library
[237] T. Lewis and L. J. Govier, "Some Properties of Counts of Events for Certain Types of Point Process,"
Journal of the Royal Statistical Society: Series B (Methodological), 26, 2, (325-337), (2018).
Wiley Online Library
[238] J. A. McFadden, "On the Lengths of Intervals in a Stationary Point Process,"
Journal of the Royal Statistical Society: Series B (Methodological), 25, 2, (500-500), (2018).
Wiley Online Library
[239] J. A. McFadden and Walter Weissblum, "Higher‐Order Properties of a Stationary Point Process,"
Journal of the Royal Statistical Society: Series B (Methodological), 25, 2, (413-431), (2018).
Wiley Online Library
[240] M. S. Bartlett, "The Spectral Analysis of Point Processes,"
Journal of the Royal Statistical Society: Series B (Methodological), 25, 2, (264-281), (2018).
Wiley Online Library
[241] Gabriel, K. J., "Comparison of Three Correlation Coefficient Estimators for Gaussian Stationary Processes,"
IEEE Trans. on Acoustics, Speech, and Signal Processing, Vol. 31, No. 4, pp. 1023-1025, Aug. 1983.
[242] Ho, Y.-C., Agrawala, A. K., "On pattern classification algorithms introduction and survey,"
Proceedings of the IEEE, Vol. 56, No. 12, pp. 2101-2114, Dec. 1968.
[243]
A Gentle Introduction to Pooling Layers for Convolutional Neural Networks https://lnkd.in/gX_wxrd
[244] Phil
Spector, An Introduction to S and S-Plus, Duxbury Press, Belmont, CA 1994.
[245]
Venables, W. N., Modern Applied Statistics with S-Plus, Springer, NY, 1997.
[246]
Statistical Tools for Nonlinear Regression: A Practical Guide with S-Plus
examples, Springer, NY, 1996.
[247] Krause, Andreas,
The Basics of S and S-Plus, Springer, NY, 1997.
[248] Dunn, K. P.,
Lower Bounds on Acceleration Estimation Accuracy, Technical Report TR-790, Lincoln Laboratory of MIT, Lexington, MA, 5 Oct. 1987.
[249] "The Scientific Computing & Instrumentation Internet Guide to Visualization Software,"
Scientific Computing & Instrumentation: The Scientific Community's Leading Source for New
Technology, Special Issue on New Directions in Scientific Software, pp. 30-31, Jan. 2001.
[250] "New Directions in Scientific Software: Controlling the Data Flow,"
Scientific Computing & Instrumentation: The Scientific Community's Leading Source for New
Technology,
Special Issue on New Directions in Scientific Software, pp. 16-18, Jan. 2001.
[251]
Grejner-Brzezinska, D. A., Da, R., Roth, C., "GPS error modeling and OTF ambiguity resolution for high-accuracy GPS/INS integrated system,"
Journal of Geodesy, Vol. 72, No. 11, pp. 626-638, Nov. 1998.
[252] Jiang Hong, Yang Youtang, and Yang Weiqin, "Exploration on Failure Diagnosis of the Electrostatic Suspended Gyro,"
IEEE Trans. on Aerospace and Electronic Systems, Corespondence, Vol. 33, No. 1, pp. 319-322, Jan. 1997.
[253]
Luenberger, D. A., "An Introduction to Observers," IEEE Trans. on Automatic Control, Nol. 16, No. 6, pp. 596-602, Dec. 1971.
[254]
Julier, S. J., Uhlmann, J. K., "A New Extension of the Kalman Filter to Nonlinear Systems,"
Proc. SPIE 3068, Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, 28 July 1997.
[255] Moore, R. K., Claassen, J. P., Lin, Y. H., "Scanning Spaceborne Synthetic Radar with Integrated Radiometer,"
IEEE Trans. on Aerospace and Electronic Systems, Vol. 17, No. 3, pp. 410-421, May 1981.
[256] M. Vidyasagar, "Computational Learning Theory: An Overview,"
Centre for Artificial Intelligence and Robotics, Bangalore, 560 001, 21 May 1993.
[257] M. Fujisaki, G. Kallianpur, H. Kunita, "Stochastic Differential Equations of
Non-linéar filtering," Osaka J. of Mathematics, Voi. 9, pp. 19-40, 1972.
[258]
R. W. Brockett and J.M.C. Clark, "On the Geometry of the Conditional Density Equation," in
Analysis and Optimization of Stochastic Systems, eds. O.L.R. Jacobs et al., Acad. Press, 1980.
[259]
R. W. Brockett, "Remarks on Finite Dimensionai Non-linear Estimation," Asterisque, 1980 (Bordeaux 1978).
[260] Daum, F. E., "New Exact Nonlinear Filters,"
Bayesian Analysis of Time Series and Dynamic Models (edited by J. C.
Spall), Chapt. 8, Marcel Dekker, New York, 1988.
[261] D. Ocone,
Topics in Nonlinear Filtering Theory, Ph.D thesis M.I.T., June 1980.
[262] S. Marcus, S. K. Mitter and D. Ocone, "Finite Dimensionai Non-linear Estimation in Continuous and Discrete Time," in
Analysis and Optimization of Stochastic Systems, eds. O.L.R. Jacobs et al., Acad. Press, 1980.
[263]
V. E. Benes, "Exact Finite Dimensionai Filters for Certain Diffusions with Non-linear Drift,"
Stochastics, Vol. 5, pp. 65-92, 1981.
[264] Sanjoy K. Mitter, "EXISTENCE AND NON-EXISTENCE OF FINITE DIMENSIONAL FILTERS,"
http://web.mit.edu/~mitter/www/publications/33_exist_nonexist_FSI.pdf
[265]
S. K. Mitter, "On the Analogy between Mathematical Problems of Nonlinear Filtering and Quantum Physics,"
Ricerche di Automatica, Vol. 10, pp. 163-216, 1980.
[266] M. Hazewinkel and S.I. Marcus, "On Lie Algebras and Finite Dimensionai Filtering,"
Stochastics, Vol. 7, pp. 29-62, 1982.
[267]
Daum, F. E., "Comments on 'Finite Dimensional Filters with Nonlinear Drift'," IEEE Trans. on
Aerospace and Electronic Systems, Vol. 34, No. 2, pp. 689-691, Apr. 1998.
[268]
Yau, S.S.-T., and Yau, S. T., "Addendum to 'Finite Dimensional Filters with Nonlinear Drift': A Response to F. E. Daum's Comments,"
IEEE Trans. on Aeropace and Electronic Systems, Vol. 34, No. 2, pp. 691-692, Apr. 1998.
[269]
Daum, F., "Practical Nonlinear Filtering with the Method of Virtual Measurements,"
Proc. of SPIE - The International Society for Optical Engineering 3163, Oct. 1997.
[270]
Paradowski, L. R., "Uncertainty Ellipses and their Application to Interval Estimation of Emitter Position,"
IEEE Trans. on Aerospace and Electronic Systems, Vol. 33, No. 1, pp. 126-133, Jan. 1997.
[271] Gerber, M. A., "Expanded Third-Order Markov Undulation Model,
AIAA Journal of Guidance and Control, Vol. 4, No. 5, pp. 495-501, Sept.-Oct. 1981.
[272] Bell, C. M., and Babitch, D., "A Systems Analysis of the Cesium Beam Atomic Clock,"
IEEE Trans. on Instrumentationand Measurement, Vol. 17, No. 2, pp. 155-166, June 1968.
[273] Wrigley, W., Woodbury, R. B., Hovorka, J., Inertial
Guidance, Institute of Aeronautical Science, N. Y. Jan. 1957.
[274]
Naval Workshop in Differential Games, Office of Naval Research, 31 July - 3 Aug. 1973.
[275] Gelb, A., and Palosky, P., "Generating Discrete Colored Noise from Discrete White Noise,"
IEEE Trans. on Automatic Control, Vol. 11, No. 1, pp. 148-149, Jan. 1966.
[276]
Soltz, J. A., Applicability of Apt Aided[Inertial System to Crustal Movement
Monitoring, Technical Report P-729, November 1978.
[277] Cruz, Jr., J. B., "Stackelberg Strategies for Multilevel Systems,"
[278] Shapiro, J. F.,
A Survey of Lagrangian Techniques for Discrete Optimization, Technical Report No. 133, Operations Research Center, MIT, May 1977.
[279] Ho, Y. C.,
The First International Conference on the Theory and Applications of Differential
Games, Division of Engineering and Applied Physics, Harvard University, Cambridge, MA, Final Report to Air Force Office of Scientific Research, Jan. 1970.
[280]
Chu, K.-C., Team Decision Theory and Information Structures in Optimal Control
Problems, Technical Report No. 622, Division of Engineering and Applied Physics, Harvard University, Cambridge, MA, Aug. 1971.
[281] Goshen-Meskin, D., Bar-Itzhack, I. Y., "On the connection between Estimability and Observability,"
IEEE Trans. on Automatic Control, Vol. 37, No. 8, pp. 1225ff, August 1992.
[282]
Bar-Itzhack, I. Y., Harman, R. R., "The MAP Spacecraft Angular State Estimation After Sensor Failure,"
https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20030020821.pdf
[283] Bar-Itzhack,
I. Y., “New Method for Extracting the Quaternion from a Rotation Matrix”, AIAA Jour. of Guidance, Control, and
Dynamics, Vol. 23, No. 6, pp. 1085-1087, Nov.-Dec. 2000.
[284]
Azor, A., I. Y. Bar-Itzhack, J. Deutschmann and R. R. Harman, “Angular-Rate Estimation Using Delayed Quaternion Measurements”,
AIAA J. of Guidance, Control, and Dynamics, AIAA J. of Guidance, Control, and Dynamics, Vol. 24, No. 3, pp. 436-443, May-Jun. 2001.
[285]
Bar-Itzhack, I. Y., “Classification of Algorithms for Angular Velocity Estimation”, AIAA J. of Guidance, Control, and
Dynamics, Vol. 24, No. 2, pp. 214-218, Mar.-Apr. 2001.
[286] Harman,
R. R. and Bar-Itzhack, I. Y., “Pseudolinear and State-Dependent Riccati Equation Filters for Angular Rate Estimation”,
AIAA J. of Guidance, Control, and Dynamics, Vol. 22, No. 5, pp. 723-725, Sept.-Oct. 1999.
[287] Olson, D. K., "Converting Earth-Centered, Earth-Fixed Coordinates to Geodetic Coordinates,"
IEEE Trans. on Aerospace and Electronic Systems, Vol. 32, No. 1, pp. 473-476, Jan. 1996.
[288] Chung, D, Lee, J. G., Park, C. G., Park, H. W.,
"Strapdown INS Error Model for Multiposition Alignment,"
IEEE Trans. on Aerospace and Electronic Systems, Vol. 32, No. 4, pp. 1362-1366, Oct. 1996.
[289]
James L. Melsa, Computational Programs for Computational Assistance in the Study of Linear Control
Theory, McGraw-Hill, NY, 1970.
[290 ] A. V. Balakrishnan, Kalman Filtering Theory, Optimization Software, Inc., Publications Division, NY, 1987.
[291]
How to Combine Oversampling and Undersampling for Imbalanced Classification:
https://machinelearningmastery.com/combine-oversampling-and-undersampling-for-imbalanced-classification/
[292] A Gentle Introduction to Cross-Entropy for Machine Learning:
https://machinelearningmastery.com/cross-entropy-for-machine-learning/
[293]
Marvin May, "MK 2 MOD 6 SINS History," The Quarterly Newsletter of The Institute of
Navigation, Vol. 14, No. 3, p. 8, Fall 2004.
[294]
Mahmood R. Azimi-Sadjadi, Tongxin Lu, Eduardo M. Nebot, "Parallel and Sequential Block Kalman Filtering and Their Implementations Using Systolic Arrays."
IEEE Trans.
on Signal Processing, Vol. 39, No. 1, pp. 137-147, Jan. 1991.
[295]
Jeff B. Burl, "Reduced Order kalman Filtering of Moving Images," Conference Record of Twenty-Second Asilimar Conference on Signals, Systems &
Computers, Pacific Grove,
CA, Vol. 2 of 2, pp. 565-567, 31 Oct.-2 Nov. 1988.
[296] Thomas Joseph Green, Jr.,
Three-Dimensional Ohject Recognition Using Laser Radar, Doctor of Philosophy, Dept. of Electrical Engineering and Computer Science, Jan. 1992.
[297] Joseph L. Doob, "The Development of Rigor in Mathematical Probability (1900-1950),"
The American Mathematical Monthly, Vol. 103, No. 7, pp. 586-596, Aug.-Sept. 1996.
[298]
Panos M. Pardalos, Leonidas S. Pitsoulis, Mauricio G. C. Resende, "Algorithm 769: Fortran Subroutines for Approximate Solution of Sparse Quardratic Assignment Problems
Using GRASP," ACM Trans. on Mathematical Software, Vol. 23, No. 2, pp. 196-208, Jun. 1997.
[298]
Pei-Chi Wu, "Multiplicative, Congruential Random-Number Generators with Multiplier
± 2K1 ± 2K2 and Modulus 2p-1,"
ACM Trans. on Mathematical Software,
Vol. 23, No. 23, pp. 255-265, Jun. 1997.
[299] Gustaf Hendeby, Performance and Implementation Aspects of Nonlinear
Filtering, Linköping studies in science and technology. Dissertation. No. 1161, Department of Electrical Engineering Linköping University, SE–581 83 Linköping, Sweden Linköping
2008.
[300] Shyam MohanM, Naren Naik,R.M.O.Gemson, M. R.
Ananthasayanam, Introduction to the Kalman Filter and Tuning its Statistics for Near Optimal Estimates and CramerRao
Bound, Technical Report: TR/EE2015/401, DEPARTMENT OF ELECTRICAL ENGINEERING INDIAN INSTITUTE OF TECHNOLOGY, KANPUR, FEBRUARY 2015.
[301] William S. Widnall, Stability of Alternate Designs for Rate-Aiding of Non-Coherent Mode of a GPS
Receiver, Intermetrics Report No. IR-302, 25 Sept. 1978.
[302] Boris Danik, "A Low-Cost Velocity Reference System for Rapid Alignment of Aircraft Inertial Platforms on a Moving Base,"
Proceedings of the IEEE 1980 National Aerospace and Electronics Conference (NAECON), pp. 608-615, 1980.
[303] Gelb, A., Course Notes Marine Inertial
Navigation, The Analytic Sciences Corporation (TASC), TASC TR-119-1, Reading, MA, January 1967. (Handles Monitor Gyro in alignment procedure for
SINS/ESGM)
[304] John E. Bortz, Micron Analysis, Vol. 1. MESGA Attitude Readout
Error, The Analytic Sciences Corporation (TASC), Technical Report AFAL-TR-72-228, Air Force Avionics Laboratory, Air Force Systems Command, Wright-Patterson Air Force Base, Ohio 45433, August 1972.
[305]
When to Use MLP, CNN, and RNN Neural Networks https://lnkd.in/gGqE_mC
Click
this link to return to the start of these reference citations.

USS Cobra Judy Radar Ship is the sister ship of
the U.S.S. Compass Island. The Compass Island had been used in
the early and mid 1970’s
as a test suite for demonstration and shake down of SSBN Navigation
changes and upgrades before deploying within the submarine fleet. Both
sister ships had little lateral “fins”
on the bottom of the hull below the water line that could be extended out horizontally from the hull to stabilize the
platform in rough seas (of a high sea state). A complete SSBN Navigation Room was present on the
Compass Island, but intentionally installed backwards from its
orientation aboard SSBN’s.
A prior NASA observation ship, the U.S.S. Vangard, replaced the Compass
Island in this role in the late 1970’s.

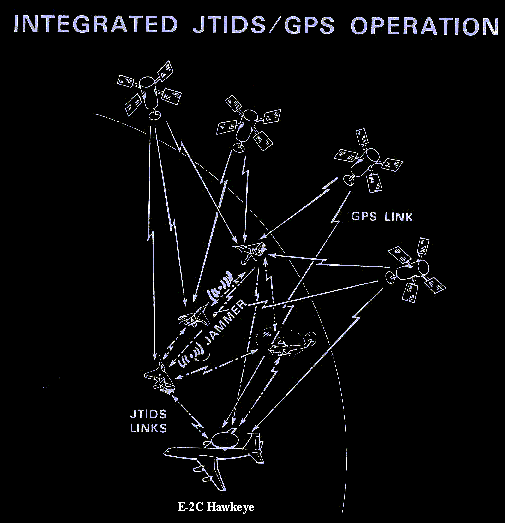

Pre- (and post-)GPS Relative Navigation (RelNav) enabled networks of
different platforms to reference both “friendlies” and enemy targets with respect
to a single common (virtual) grid using the L-band JTIDS (time-slotted
and frequency hopped from 960 MHz to 1215 MHz, with gaps imposed for TACAN
and IFFN). This capability was especially
useful when all participants were at sea and far from any geographic landmarks
of absolute location. The grid tended to move and rotate slightly. It’s location
was dictated by the Navigation Controller (NC), the platform having the
best navigation accuracy (as a self-assessment), but in lieu of the demise of
the original NC, the NC was replaced by the next best platform in
this role to avoid possessing a single point vulnerability. JTRS
(pronounced Jitters) is
slated to replace JTIDS as an entirely software radio system (with its own
unique set of problems yet to be solved). JTIDS included NTDS/ATDS.
Air Force JTIDS used DTDMA protocol without RelNav. Navy
version was TDMA with RelNav. Marine version of JTIDS was PLRS. Reed Solomon
Code throughout. GPS uses Gold Code in two flavors or cycle lengths (to
be upgraded).

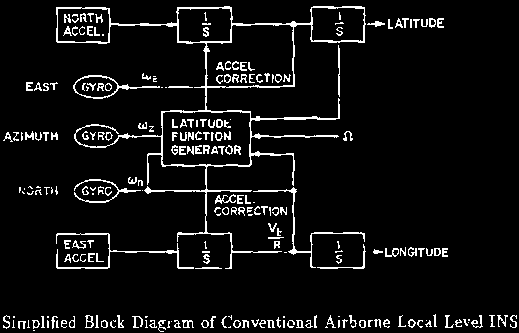

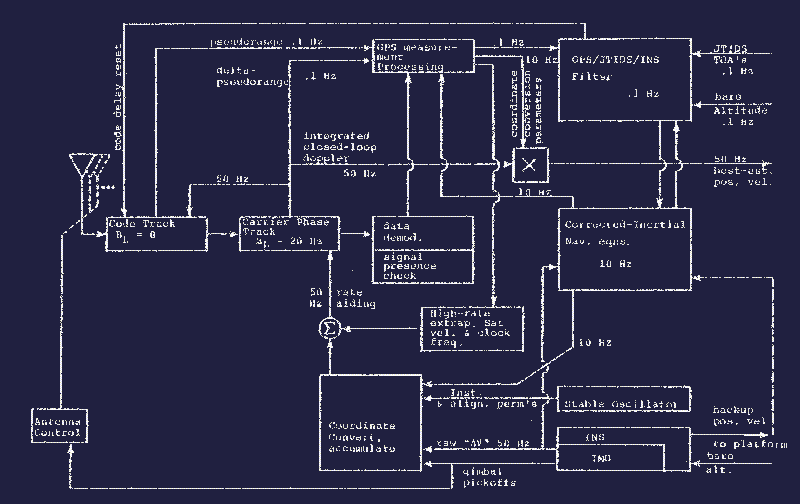
Hybrid High-Rate Output Candidate Design for JTIDS/GPS/INS
Integration and INS Navaid Selection.




Sam Blackman (Raytheon/Hughes), the (late) Oliver
Drummond, Yaakov Bar-Shalom (UCONN), and Rabinder Madan.
http://www.ieee.org/about/awards/bios/picard_recipients.html
Blazers of the exciting area of multi-sensor\multi-target tracking (sometimes pursued even in
clutter) [related to optimal resource allocation and solved by invoking Munkres or the
Hungarian or Jonker- Volgenent- Castanon’s (J-V-C) or Murty’s
(1968) or Sam Blackman's Multi- Hypothesis Testing (MHT) algorithms. The first 3 techniques are all from the Operations Research
area; the last is based on Bayesian Statistical analysis.
Not shown here: Prof. David Castanon
(Boston University) and Charles Morefield (originally of Aerospace
Corporation in the 1970’s when he posed multi-target tracking as a 0-1 Integer
Programming Problem, more recently Chairman of the Board at Alphatech (after Michael
Athans stepped down and went to Portugal) before Alphatech
became part of BAE in Burlington, MA), and Thomas
Kurien (Raytheon). Also see Particle Filter variations in: Vermaak,
J., Godsill, S. J., Perez, P., “Monte-Carlo Filtering for
Multi-Target Tracking and Data Association,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 41, No. 1, pp.
309-331, Jan. 2005. Also see Miller, M. L., Stone, H, S., Cox, I. J., “Optimizing
Murty’s
Ranked Assignment Method,”
IEEE Trans. on Aerospace and Electronic Systems, Vol. 33, No. 7, pp.
851-862, July 1997. Another: Frankel, L., and Feder, M., “Recursive
Expectation-Maximizing (EM) Algorithms for Time-Varying Parameters with
Applications to Multi-target Tracking,”
IEEE Trans. on Signal Processing, Vol. 47, No. 2, pp. 306-320, February
1999. Yet another: Buzzi, S., Lops, M., Venturino, L., Ferri, M., “Track-before-Detect
Procedures in a Multi-Target Environment,”
IEEE Trans. on Aerospace and Electronic Systems, Vol.
44, No. 3, pp. 1135-1150, July 2008.


Fourth
ONR/GTRI Workshop on Target Tracking and Sensor Fusion, Naval Postgraduate
School, Monterey, CA, 17 May 2001.Notice the guy (i.e., THK III) apparently in sun glasses
(actually transitions) in the back
row there (left of center, as always).

Lockheed Martin’s Paveway
II Dual Mode Laser-Guided Bomb (DMLGB), which uses both laser-guided and
inertial/GPS guidance, has achieved the U.S. Navy's initial operational
capability and is now preparing for operational employment.